組織の複雑な課題を解決するために、データ分析の重要性が高まっています。その中でも、構造方程式モデリング（SEM: Structural Equation Modeling）は、組織内の様々な要因の関連性を理解するための手段として有用です。

SEMは、組織内の多様な要因がどのように関連し合い、成果指標にどのような影響を与えているかを、視覚的かつ数値的に示すことができます。しかし、SEMの結果を正しく解釈し、活用するためには、様々な指標を理解し、その見方を習得する必要があります。

本コラムでは、人事の皆さまを対象に、SEMの分析結果の読み方を解説します[1]。特に、各指標の意味と解釈に焦点を当て、架空の組織サーベイの例を用いながら説明していきます。

モデルとは何か

SEMの解説に入る前に、「モデル」について理解しておくことが大切です。

モデルとは、現実世界の複雑な現象や関係性を、単純化・抽象化して表現したものです。私たちが理解したい現象について、「こういう仕組みになっているのではないか」という仮説を図や数式で表したものがモデルです。

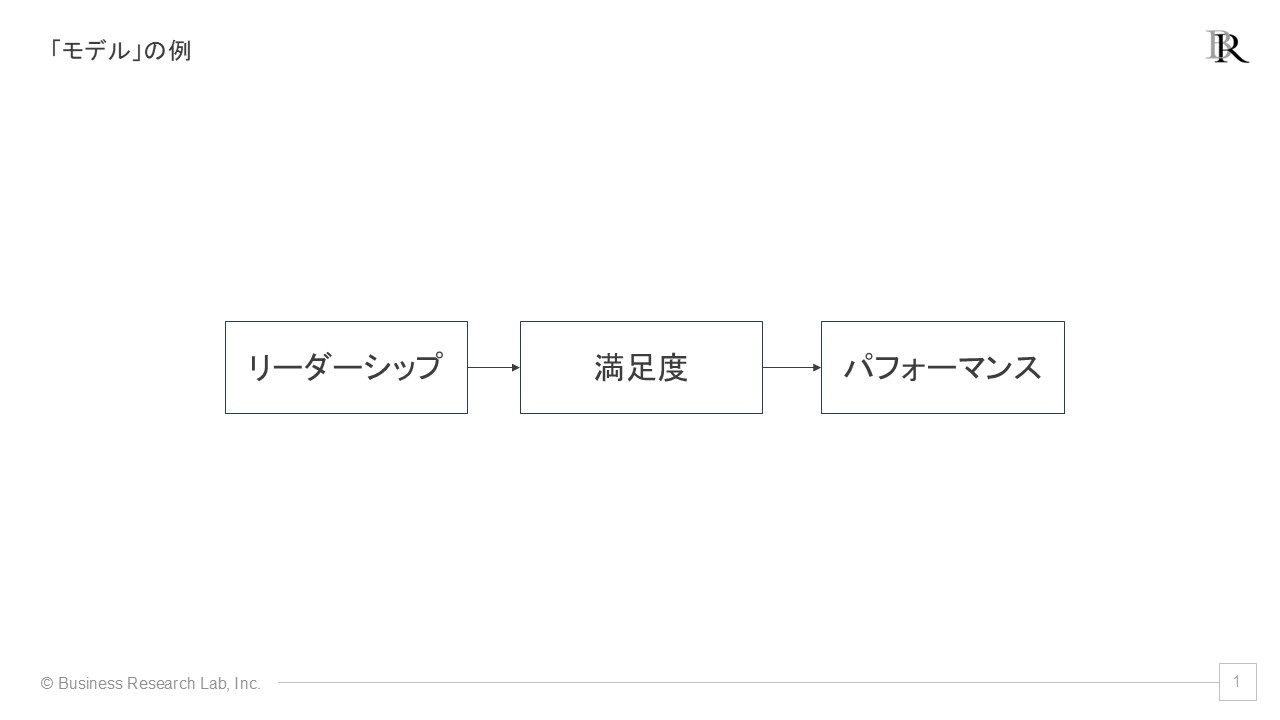
例えば、「リーダーシップが従業員の満足度に影響を与え、それがパフォーマンスにつながる」というシンプルなモデルを考えてみましょう。これを図で表すと次のようになります。

このモデルは、現実世界の複雑な関係性を単純化したものです。実際には、リーダーシップや満足度、パフォーマンスにはさまざまな要素が含まれており、それらの関係性も複雑です。しかし、このようにシンプルに捉えることで、私たちは複雑な現象における本質的な部分に注目し、理解を深めることができます。

SEMは、こうしたモデルを統計的に検証し、モデルが現実のデータとどの程度一致しているかを評価する手法です。SEMを用いることで、私たちの仮説（モデル）が現実世界をどの程度うまく捉えられているかを数値で表現することができます。

架空の組織サーベイ例

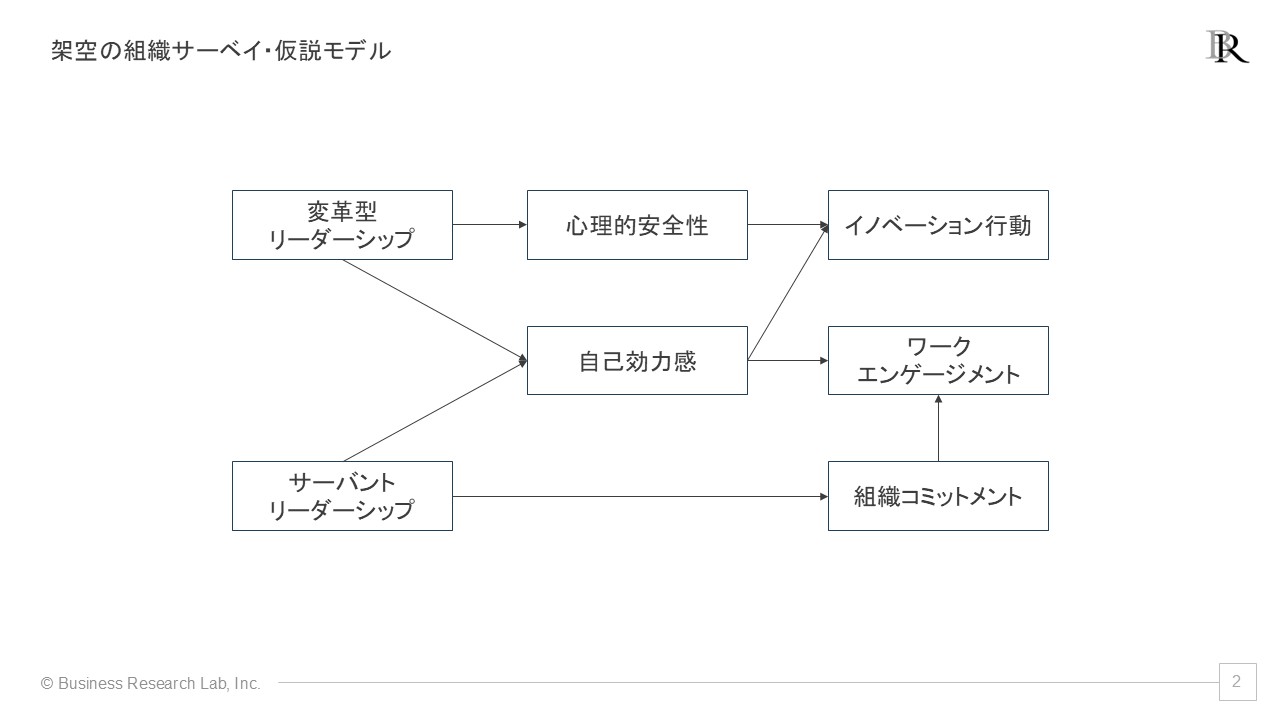
それでは、具体例を用いてSEMの結果の読み方を見ていきましょう。次のような、ワークエンゲージメントに関する架空の仮説モデルを考えてみます（これはあくまで、本コラムにおける説明のためだけに作成した架空のモデルです）。

このモデルを理解するために、各概念の定義を確認しましょう。

• 変革型リーダーシップ：部下に対して明確なビジョンを示し、個別の配慮を行いながら、知的刺激を与え、部下の成長を促すスタイル
• サーバントリーダーシップ：部下の成長と幸福を優先し、奉仕の姿勢でチームを導くスタイル
• 心理的安全性：チーム内で自分の意見や考えを表現しても、否定的な反応を恐れる必要がないと感じること
• 自己効力感：課題や目標を達成する能力が自分にはあるという自信
• イノベーション行動：新しいアイデアを生み出し、それを実現するために行動すること
• 組織コミットメント：従業員が組織に対して感じる愛着や帰属意識、組織の目標や価値観との一体感
• ワークエンゲージメント：従業員が自身の仕事にいきいきと取り組み、打ち込んでいること

このモデルでは、次の仮説を立てています。

• 変革型リーダーシップとサーバントリーダーシップが心理的安全性、自己効力感、組織コミットメントに関連する
• 心理的安全性と自己効力感がイノベーション行動に関連する
• 自己効力感と組織コミットメントがワークエンゲージメントに関連する

SEMの分析結果と解釈

このモデルに基づいたSEM分析結果を見ていきましょう。分析結果も架空のものとなります。その点、ご注意ください。

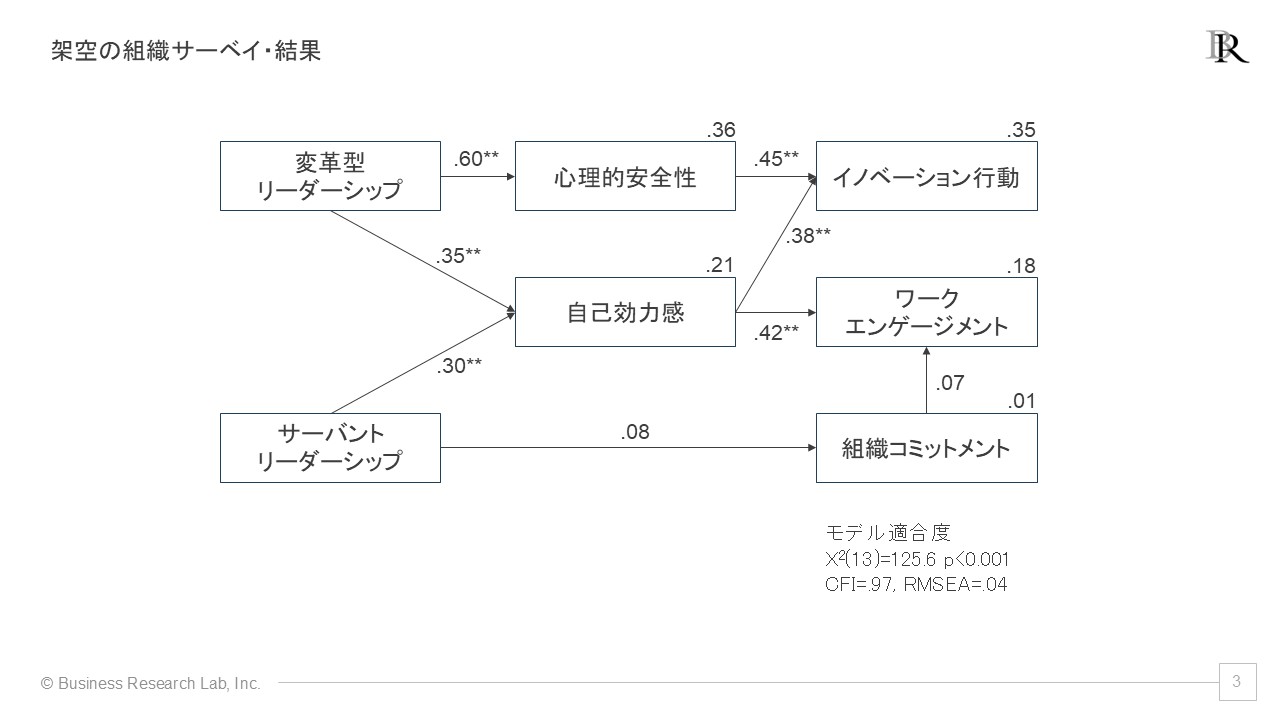
この分析結果について、指標ごとに何を意味しているのかを解釈していきます。

モデル適合度

モデル適合度は、モデルが実際のデータにどの程度合っているかを示す指標です。仮説（モデル）が現実のデータをどれだけうまく捉えているかを表します。

例えば、「リーダーシップが従業員の満足度に影響を与え、それがパフォーマンスにつながる」というモデルを考えたとします。このモデルが実際の組織サーベイのデータとどの程度一致しているかを示すのがモデル適合度です。モデル適合度が高ければ、仮説が現実をうまく捉えられていると考えられます。逆に低ければ、モデルは現実のデータと合っておらず見直しが必要です。

分析結果の中にはいくつかの適合度指標が出てきています。それぞれの意味するところを見ていきましょう。

カイ二乗検定

分析結果において、カイ二乗値（χ²）は125.6で、自由度は13、p値は0.001未満となっています。

カイ二乗検定は、「モデルで推定される指標間の関連性と実際のデータで示される指標間の関連性が、完全に適合している」という帰無仮説を検定します[2]。一般的に、p値が.05以上であれば、モデルと観測データの間に統計的に有意な乖離がないと判断します[3]。通常の帰無仮説検定では、p値が.05以下で統計的に有意であるかを確認します。一方、ここでは「モデルとデータに乖離がない＝合っている」ことを帰無仮説において検証しているため、帰無仮説が棄却されない結果である「統計的に有意でない」ことを確認します。

しかし、この結果では p値が0.001未満であり、帰無仮説が棄却される結果となっています。注意すべき点として、カイ二乗検定はサンプルサイズに非常に敏感で、サンプルサイズが大きい場合、わずかな不適合でも統計的に有意になる可能性があるため、p値の解釈には注意が必要です。

また、カイ二乗検定はモデルが現実のデータに「完全に」適合していることを前提にしているため、現実の分析ではカイ二乗検定の結果だけに依存せず、他の適合度指標も併せて評価する必要があります。

CFI

CFI（Comparative Fit Index）は、構築したモデルと、全ての変数間に関連がないと仮定した最も基本的なモデルとを比較し、構築したモデルがどれほど改善されているかを示す指標です。

CFIの値は0から1の間をとり、1に近いほど良いモデルであることを意味しています。一般的に.90以上なら許容でき、.95以上が良好とされています。

架空の分析結果においては、CFIが.97という値を示しています。これは良好な値であり、このモデルがデータをよく説明していることを表しています。

これは、構築したモデルが、「全ての変数間に関連がない」と仮定したモデル（独立モデル）と比べて、データへの適合度が大きく改善されていることを示しています。今回のモデルは、データの特徴をある程度正確に捉えていると言えるでしょう。

RMSEA

RMSEA（Root Mean Square Error of Approximation）は、分析で推定する各種係数の多さなどモデルの複雑さを考慮に入れた上で、モデルとデータの乖離を評価する指標です。

RMSEAは0に近いほど良いモデルであることを示し、一般的に.05以下であれば良好、.10以下であれば許容可能とされます。

分析結果では、RMSEAが0.04という値になっています。これは良好な値であり、このモデルがデータとよく適合していることを表しています。具体的には、このモデルとデータの間の平均的な誤差が小さいことを意味します。

これらのモデル適合度の結果を総合すると、カイ二乗検定の結果は好ましくないものの、他の適合度指標は良好な値を示しています。したがって、今回のモデルは実際のデータとよく合っていると解釈できます。

パス係数

パス係数は、SEMの結果において、変数間を結ぶ矢印上に表示されます。パス係数は-1から1の間の値をとり（標準化係数の場合）、次のように理解します。

• 正の値：一方の変数が増加すると、もう一方の変数も増加する関係
• 負の値：一方の変数が増加すると、もう一方の変数は減少する関係
• 絶対値が大きいほど影響が強いことを示す

例えば、標準化パス係数が.50の場合、他の変数の影響を制御した上で、一方の変数が1標準偏差増加すると、もう一方の変数が0.5標準偏差増加すると予測されます[4]。

今回の分析結果では、多くのパスが統計的に有意ですが、一部のパスは有意ではありませんでした[5]。各パスの解釈を見ていきます。

• 変革型リーダーシップから心理的安全性へのパス係数は「.60**」となっていますが、これは強い正の関連を示しており、統計的に有意です。変革型リーダーシップが1標準偏差増加すると、心理的安全性が.60標準偏差増加すると解釈できます。
• 変革型リーダーシップから自己効力感へのパス係数は「.35**」ですが、これは中程度の正の関連を示しており、統計的に有意です。変革型リーダーシップが1標準偏差増加すると、自己効力感が35標準偏差増加します。
• サーバントリーダーシップから自己効力感へのパス係数は「.30**」であり、中程度の正の関連を表しています。統計的に有意な結果です。サーバントリーダーシップが1標準偏差増加すると、自己効力感が30標準偏差増加します。
• サーバントリーダーシップから組織コミットメントへのパス係数は「.08」です。これは弱い正の関連を示していますが、統計的に有意ではありません。サーバントリーダーシップは組織コミットメントと直接的な関連がない可能性があります。
• 心理的安全性からイノベーション行動へのパス係数は「.45**」であり、中程度から強い正の関連となっています。統計的に有意です。心理的安全性が1標準偏差増加すると、イノベーション行動が45標準偏差増加するという関係です。
• 自己効力感からイノベーション行動へのパス係数は「.38**」で、これは中程度の正の関連で、統計的に有意です。自己効力感が1標準偏差増加すると、イノベーション行動が38標準偏差増加します。
• 自己効力感からワークエンゲージメントへのパス係数は「.42**」です。中程度から強い正の関連を示しており、統計的に有意です。自己効力感が1標準偏差増加すると、ワークエンゲージメントが42標準偏差増加します。
• 組織コミットメントからワークエンゲージメントへのパス係数は「.07」ですが、非常に弱い正の関連となっており、統計的に有意ではありません。組織コミットメントはワークエンゲージメントとの間で直接的な関連がないと考えられます。

これらのパス係数を総合的に見ると、どのような解釈ができるでしょうか。

まず、変革型リーダーシップは心理的安全性と自己効力感との間で強い正の関連にあります。サーバントリーダーシップも自己効力感に正に関連しています。リーダーシップの重要性がうかがえます。しかし、サーバントリーダーシップと組織コミットメントとの関連は統計的に有意ではありませんでした。

心理的安全性と自己効力感がイノベーション行動との間で重要な関連を示しています。自由に意見を言える環境と自分の能力に対する自信が、新しいアイデアの創出と実行を促進し得るということです。

自己効力感がワークエンゲージメントと重要な関連にあります。しかし、組織コミットメントとワークエンゲージメントの関連は統計的に有意ではありませんでした。

決定係数

決定係数（R²）は、ある変数の分散（ばらつき）がモデル内の他の変数によってどの程度説明されているかを示します。0から1の間の値をとり、1に近いほど、その変数の変動がモデル内の他の変数によってよく説明されています。

例えば、ある変数のR²が.50だった場合、その変数の変動の50%がモデル内の他の変数によって説明されていると解釈します。残りの50%は、モデルに含まれていない他の要因や測定誤差によるものと考えられます。

今回の分析結果のR²を見てみましょう。

• 心理的安全性のR²は「.36」です。心理的安全性の変動の36%が変革型リーダーシップによって説明されています。
• 自己効力感のR²は「.21」であり、自己効力感の変動の21%が変革型リーダーシップとサーバントリーダーシップによって説明されていることを意味します。
• 組織コミットメントのR²は「.01」になっています。組織コミットメントの変動のわずか1%しかサーバントリーダーシップによって説明されていません。これは低い値であり、組織コミットメントを説明するためには、このモデルに含まれていない他の重要な要因がある可能性が高いと言えます。
• イノベーション行動のR²は「.35」です。イノベーション行動の変動の35%が心理的安全性と自己効力感によって説明されています。
• ワークエンゲージメントのR²は「.18」であり、ワークエンゲージメントの変動の18%が自己効力感と組織コミットメントによって説明されていることを表します。

今回のモデルは特に心理的安全性（R²=.36）とイノベーション行動（R²=.35）をよく説明できています。加えて、自己効力感（R²=.21）についてもある程度の説明力を持っています。

ただし、組織コミットメント（R²=.01）については、モデルの説明力が低いでしょう。この変数に影響を与える重要な要因が、現在のモデルに含まれていない可能性が高いと考えられます。

まとめ

構造方程式モデリング（SEM）は、組織の複雑な課題を紐解く際に役立ちます。本コラムでは、人事の皆様に向けて、SEMの分析結果をどう読み解き、活用するかを紹介しました。

SEMの結果を理解する鍵は、主に3つの指標にあります。

• モデル適合度：CFIやRMSEAなどの数値が、仮説（モデル）が現実のデータとどれほど合っているかを教えてくれます。例えば、CFIが95以上なら、モデルの説明力が高いと判断できます。
• パス係数：変数間の関係の強さと方向性を示します。例えば、リーダーシップとエンゲージメントの間のパス係数が.50だった場合、リーダーシップの向上がエンゲージメントの上昇につながる可能性が高いと解釈できます。
• 決定係数：各変数がモデル内の他の変数によってどの程度説明されているかを示します。例えば、エンゲージメントのR²が.40なら、モデルに含まれる要因がエンゲージメントの40%を説明していると理解できます。

これらの指標を見ることで、組織の中で何が起きているのかを理解するきっかけとなります。例えば、「リーダーシップ研修には本当に効果があるのか」「どのような職場環境がイノベーションを促進するのか」といった疑問に、データに基づいたヒントを見出すことができます。

ただし、SEMの結果を解釈する際は、数字だけでなく組織の文脈も考慮することが大切です。また、SEMは相関関係を示すものであり、因果関係を直接証明するものではないことにも注意が必要です。

SEMは複雑な分析手法ですが、その結果を理解し活用することで、組織の成長と従業員の幸せにつながる、効果的な施策を生み出すことができるでしょう。本コラムが、データ活用の一助となれば幸甚です。

脚注

[1] 構造方程式モデリングそのものの説明については当社セミナーレポートが参考になります。

[2] 指標間の関連性は、厳密には「分散共分散行列」を指します。

[3] これはモデルが適合していることを直接的に示すものではありません。

[4] ただし、これは他の変数の影響を制御した上での関連を示しています。

[5] 今回の架空の分析結果においては、一部を除き、パス係数は1％水準で統計的に有意となっています。

---

執筆者

伊達 洋駆　株式会社ビジネスリサーチラボ 代表取締役
神戸大学大学院経営学研究科 博士前期課程修了。修士（経営学）。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、組織サーベイや人事データ分析のサービスを提供している。著書に『60分でわかる！心理的安全性 超入門』（技術評論社）や『現場でよくある課題への処方箋 人と組織の行動科学』（すばる舎）、『越境学習入門 組織を強くする「冒険人材」の育て方』（共著；日本能率協会マネジメントセンター）などがある。2022年に「日本の人事部 HRアワード2022」書籍部門 最優秀賞を受賞。東京大学大学院情報学環 特任研究員を兼務。