ビジネスリサーチラボは、2024年11月にセミナー「指標の関係性を捉えるデータ分析のエッセンス：相関・回帰分析の技法」を開催しました。

人事領域のデータ分析において、様々な指標間にどのような関連があるか探る分析手法は重宝されています。その代表例が、相関分析と回帰分析です。例えば、「従業員の満足度と離職意思の関連を相関分析で検証する」、「従業員同士のコミュニケーションを高めることはエンゲージメントに有意義か、回帰分析で検証する」というように、指標間の関連性をデータに基づいて検証することができます。

これらの手法を学ぶことで、成果指標を変えるために有効な要因をデータから見出すことができるのです。本セミナーでは、相関係数と回帰係数が示す結果の基本的な理解に加えて、それらをどのように実務で活用できるか解説しました。

※本レポートはセミナーの内容を基に編集・再構成したものです。

相関分析の特徴-1：対応関係を「量的」に理解できる

対応関係の「種類」

黒住：

私のパートでは、相関分析について説明します。相関分析とは、端的に言うと「2つの指標間の対応関係を調べる手法です。さらに踏み込んで、「何が分かるのか」「何ができるのか」というエッセンスを紹介しますので、実務の中でより有効な活用につなげていただければ幸いです[1]。

まず１つ目のパートとしては、相関分析を通じて、２つの指標の対応関係を「量的」に理解できるという点を紹介します。相関分析では、指標間の関係性を「種類」と「強さ」として示します。相関係数「r」と呼ばれる数値で、次の3種類の関係性を表すことができます。

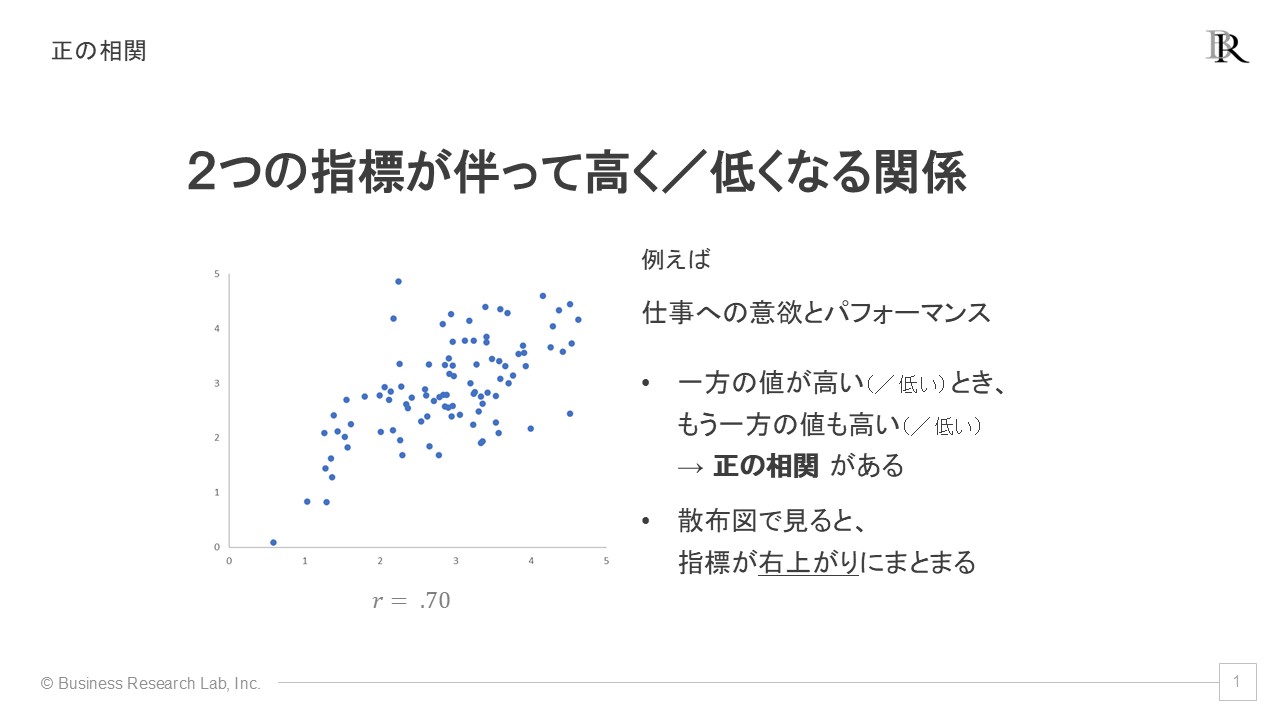
1つ目は「正の相関」です。これは、2つの指標が伴って高くなる、または低くなる関係性を指します。たとえば、「仕事への意欲」と「パフォーマンス」の関係性です。仕事への意欲が高い人は、パフォーマンスも高くなる傾向があります。一方で、意欲が低い場合は、パフォーマンスも低くなることが予想されます。

このような正の相関を示すデータは、散布図で確認できます。散布図では、2つの指標の値が右上がりの分布を示す場合に、正の相関があると言えます。

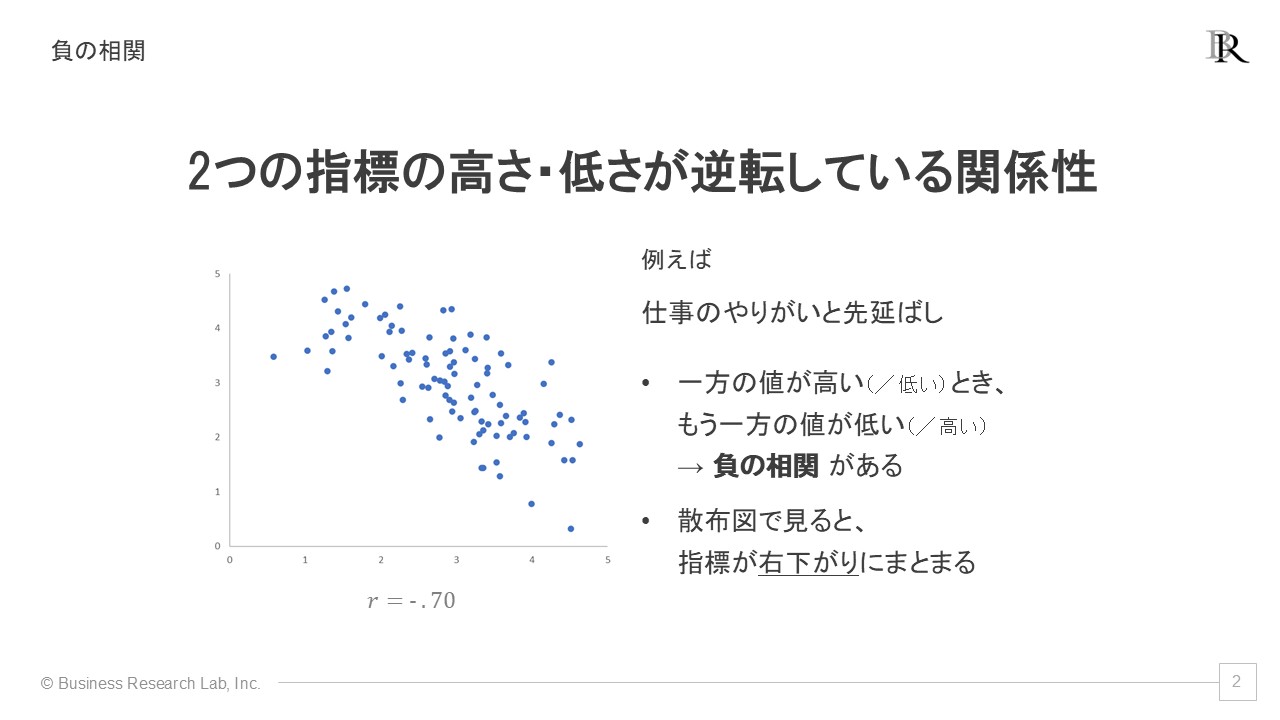
2つ目は「負の相関」です。これは、1つの指標が高くなると、もう1つの指標が低くなるような関係性です。たとえば、「仕事のやりがい」と「先延ばし」の関係が該当します。やりがいを感じる仕事であれば熱心に取り組むので、先延ばしされる可能性が低くなります。このような場合、散布図ではデータが右下がりの分布を示します。

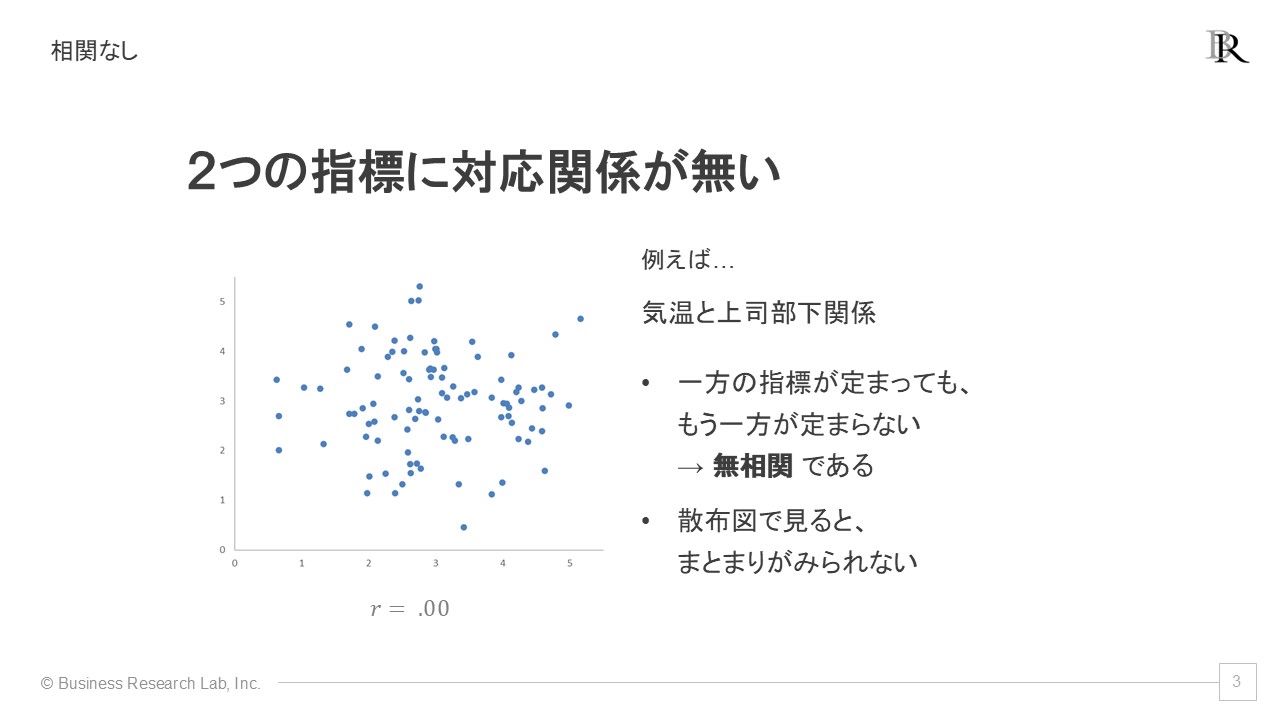
3つ目は「相関がない」場合です。この場合、1つの指標の値がもう1つの指標の値と何の関係も持たない状態を指します。たとえば、「気温」と「上司と部下の関係性」の関係です。気温が高いからといって、上司と部下の関係性が良くなったり悪くなったりするわけではありません。このような関係がない状態を「無相関」と呼びます。散布図では、データがばらばらに分布しており、まとまりがない場合に無相関であると判断できます。

対応関係の「強さ」

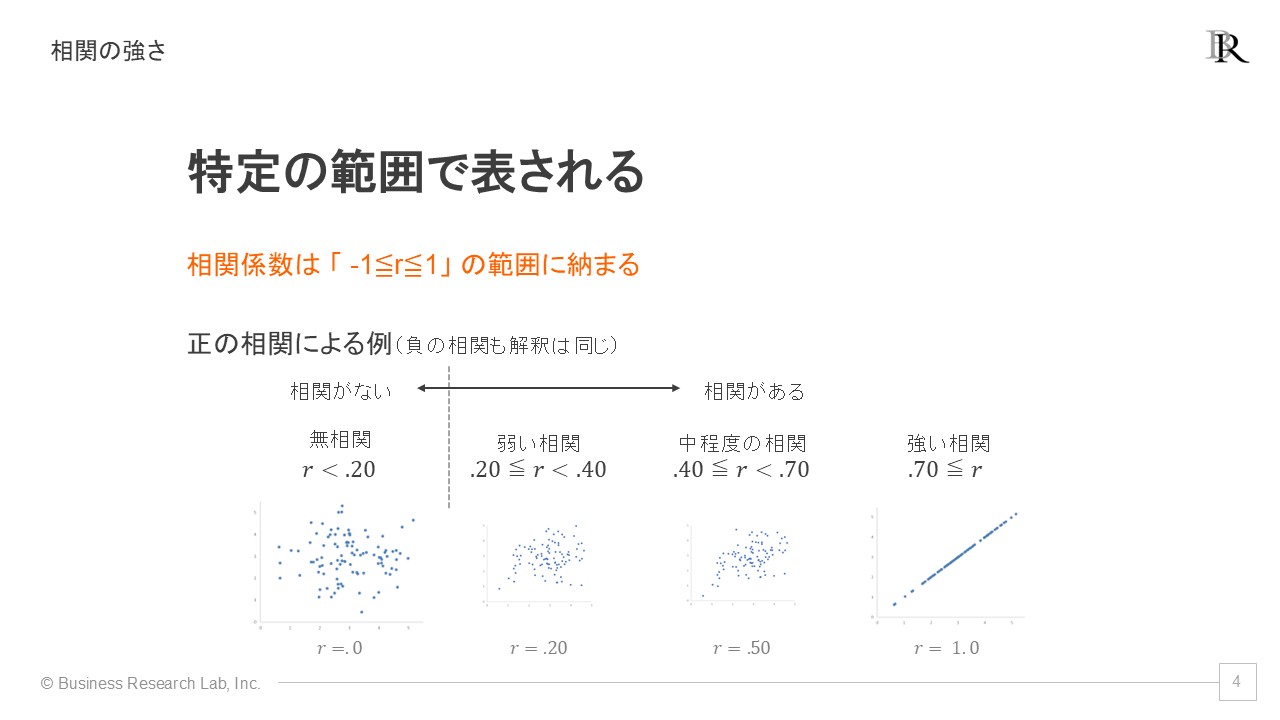
ここまで3つの対応関係について説明してきましたが、相関係数は「その対応関係がどの程度強いのか」ということも表すことができます。相関rは、「-1から1」の範囲内に収まるように計算されます。

加えて、この範囲内でどの程度の値を、強いあるいは弱いとみなすのか、基準も提案されています。正の相関を例にとると、以下のような基準が示されています[2]。負の相関についても、正負が逆転するものの、範囲の基準は同じです。

• .00～.20：無相関
• .20～.40：弱い相関
• .40～.70：中程度の相関
• .70～00：強い相関

では、相関係数の強さについて、その例を図と併せて確認してみましょう。左から右に向かって4つの図が並んでおり、それぞれに具体的な基準を併記しています。

一番左側の図は「無相関」を示しており、データは大きく散らばっています。しかし、右に進むにつれてデータがまとまっていき、1本の線に近づいていく様子がわかります。このように、相関が弱い場合は、一方の値が決まったとしても、他方はさまざまな値を取りえます。しかし、相関が強い場合は、一方の値からもう一方の値を対応付けることができるようになります。

注意が必要なのは、相関は「対応関係」を示すものであり、「傾き」とは異なるという点です。傾きとは、「一方の指標が変化する量に対して、もう一方がどの程度変化するか」を示すものです。その詳細は、後半の能渡さんのパートで解説されますが、両者が異なるということは理解しておくことが重要です[3]。

相関分析の特徴-2：対応関係を「客観的」に検討できる

相関係数は比較が可能

2つ目のパートとして、対応関係を「客観的に」検討できるという点についてご説明いたします。たとえば、「仕事に意欲のある人はパフォーマンスも高そうだ」といった実感を、普段の業務で持つことがあるでしょう。このような実感や予測を、相関分析を実施することで、客観的なデータとして示すことができます。

客観的な検討に関する具体的なポイントを、大きく2つに分けて説明いたします。まず、相関係数は「比較」できるという点です。相関係数rが-1から1の範囲で表されること、その値には強さの基準があることをご確認いただきました。さらに、その値には、測定が何段階での回答だったかという単位や、回答者の人数の影響も計算によって除外されます。これにより、たとえば相関係数0.8は「強い相関」であり、0.3と比べても強いと判断できます。

推測統計の応用

もう一つのポイントとして、「推測統計を活用できる」という点についてご説明いたします。推測統計とは、統計的な手法を用いて「得られた結果が偶然ではないことを示す」手段です[4]。相関分析自体は推測統計を使わなくても計算できますが、推測統計を併用することで、結果の確からしさを確認できるという利点があります。この推測統計を活用することで得られるメリットについて、以下で詳しくご説明いたします。

推測統計を活用するメリットは大きく2つあります。1つ目のメリットは、得られた結果を他の調査対象にも応用できるという点です。推測統計によって「統計的に有意である」という結果が確認された場合、その結果は偶然の産物ではなく、他の類似した集団でも同じような結果が得られる可能性が高いと判断できます。

たとえば、仮想的な例として「内定者調査」を考えてみましょう。今年度の内定者に対して、自社の魅力についての調査を行った結果、以下のような相関が確認されたとします。

• 「メンターからのアドバイス」と「自社の魅力」の相関係数が0.3（弱い相関）
• 「同期との交流頻度」と「自社の魅力」の相関係数が0.6（中程度の相関）

どちらも「統計的に有意」であるという結果が得られた場合、この結果は来年度の内定者にも同じように適用できる可能性が高いと考えられます。すると、このデータを基に、「来年度は同期同士の交流会をさらに充実させることで、内定者を惹きつける施策を検討しよう」といった具体的な行動につなげることができます。

2つ目のメリットは、得られた分析結果の判断基準を増やせるという点です。たとえば、強い相関係数であっても統計的に有意でない場合、他の回答者に同じ結果が得られるとは限りません。逆に、弱い相関であっても、統計的に有意であれば他の同様のサンプルにおいて再現される可能性が高いのです。つまり、得られた結果を、今後の施策に生かすかどうかという判断材料にもなるのです。

相関分析時の注意点

「選抜効果」に注意

最後に、相関分析を実施する際の実践上の注意点をご紹介します。実は、分析の方法を正しく理解していても、実態を誤って解釈してしまうリスクがあります。今回は、その具体例として、2つの注意点をご紹介します。

注意点の１つ目は、「選抜効果」です。これは、特定の基準で回答者を選別することによって、相関係数が弱くなることです。つまり、考慮するべき相関を見落としてしまうリスクがあるのです。

たとえば、「学習意欲」と「パフォーマンス」という2つの指標について考えてみます。一般的に、学習意欲が高い人はパフォーマンスも高い傾向があると予想されます。しかし、調査対象を「研修に参加した人」に限定してしまうと、どうなるでしょうか。

研修に参加する人は、学習意欲が高い層に偏っている可能性があります。その結果、パフォーマンスが低い層や学習意欲が低い層が調査対象から外れてしまいます。これにより選抜効果が生じ、学習意欲とパフォーマンスの関係性が十分に反映されなくなる可能性が高いといえます。

「第三の変数」に注意

注意点の２つ目は、「第3の変数」の存在です。「第3の変数」とは、注目している2つの指標がある場合に、それらに影響を与える別の指標のことです。この指標があると、２つの指標に本来存在しないような、「見せかけ」の対応関係が算出されるため、実態をミスリードしてしまうリスクがあります。

具体例として、研修中に積極的に相談する人の方が、研修後の課題で良い成績を収める傾向が見られたとします。この結果から「相談をすること」は「課題成績の向上」に関連していると考えられるかもしれません。

しかし、仮に「親密な関係性」という第三の変数があった場合はどうでしょう。研修の参加者は、講師と親密であれば相談しやすくなり、親密な関係であれば、意図せず課題の答えを伝えてしまうかもしれません。これはもちろん架空の例ですが、このような状況では「相談回数」と「課題成績」の間に見られる相関は、親密さという第3の変数によって生み出されたものに過ぎない、ということになります。

具体的な対策

では、2つ注意点に対して、どのように対処すべきかを説明します。まず、「選抜効果」への対策についてです。この効果に対応するためには、さまざまな回答や回答者のデータを収集することが重要です。様々な回答者を統合したうえでの結果と、一部に限定した結果を比較することが有効です。これにより、選抜効果が発生しているかどうか、全体的な結果との違いを確認することができます。

次に、「第3の変数」への対策です。この場合、問題となりそうな第3の変数をあらかじめ測定し、そのデータを分析に組み込むことが重要です。これにより、注目している2つの指標が本当に関係しているのか、それとも第3の変数の影響を受けているのかをより正確に判断することができます[5]。

そして、これら個別の対策に共通するポイントが、サーベイへの「準備」の段階です。様々な回答者へ調査することや、第3の変数を分析に取り入れるにも、「分析」の段階から対応することは難しいのです。そのため、サーベイの準備段階で、どのような影響が想定されるのかをあらかじめ検討し、サーベイを設計することが重要なのです。

回帰分析の技法

成果指標と影響指標

能渡：

本題に入る前に、このパートで用いる語句について先に整理しておきます。

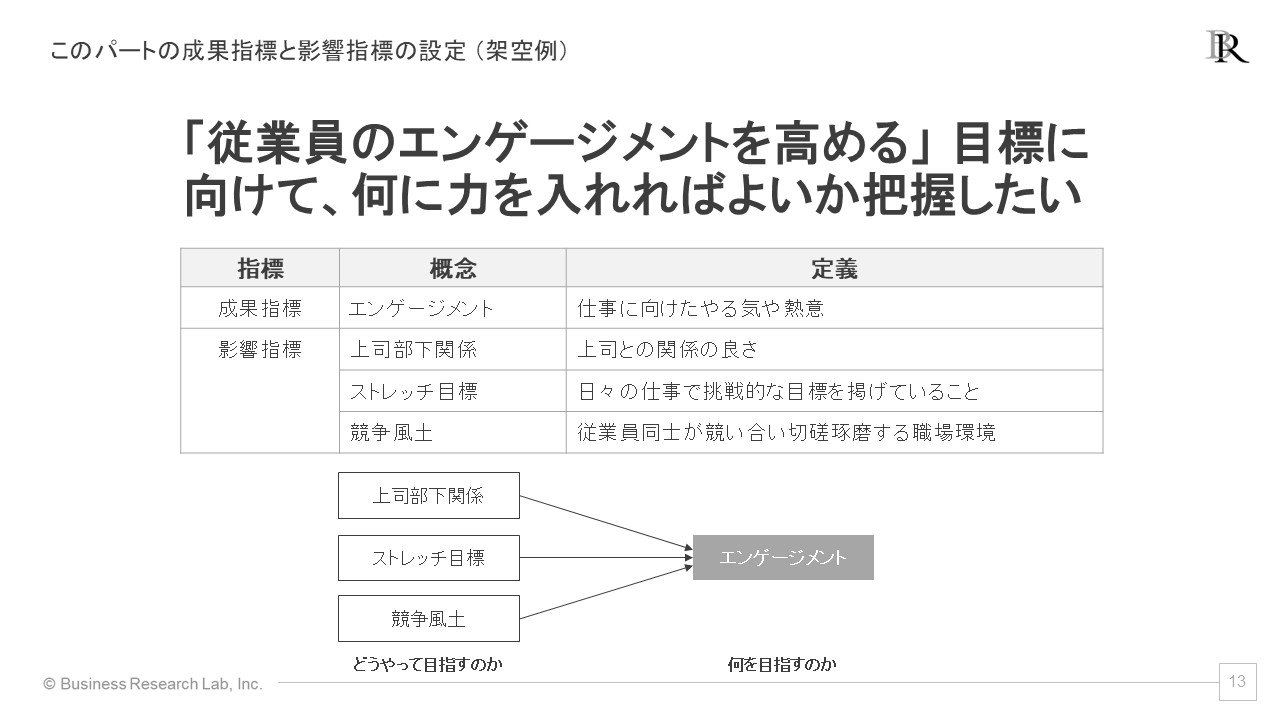
まず、「成果指標」と「影響指標」という用語を使います。成果指標とは、組織や個人が目指すべき状態や目標を表す指標で、具体的には、サーベイを通して「何を目指すのか」を示すものです。一方、影響指標とは、その成果指標に影響を与える要因を示す指標であり、成果指標に向けて「どうやって目指すのか」を示すものです。

回帰分析を理解するうえで、成果指標と影響指標を区別して捉えることが重要となります。例として、架空のサーベイを想定します。このサーベイの目的は、「従業員のエンゲージメントを高めること」であるとし、ここではエンゲージメントを「仕事に対するやる気や熱意」と定義します。そして、このエンゲージメントという成果指標を高めるために、どのような要素に力を入れればよいかを調べることをサーベイの目的とします。

加えて、エンゲージメントという成果指標に対して、影響指標は次の3つを取り上げたとしましょう。1つ目は「上司部下関係」、つまり上司との良好な関係性です。2つ目は「ストレッチ目標」、日々の業務において挑戦的な目標を設定しているかどうかです。そして3つ目は「競争風土」、従業員同士が切磋琢磨する職場環境です。これらがエンゲージメントを高めるのに寄与するのではないかという仮説のもと、分析を進めていく状況を考えます。

このように回帰分析は、「成果指標を高める影響指標は何か」と、原因となる影響指標とその結果となる成果指標をそれぞれ分けて捉えることが特徴です。

単回帰分析とは

このような指標間の関連性を分析するうえで、まず用いられるのが相関分析です。相関分析は、2つの指標間の対応関係を数値化するものであり、影響指標と成果指標の関連性を検証するために非常に重要な分析手法です。

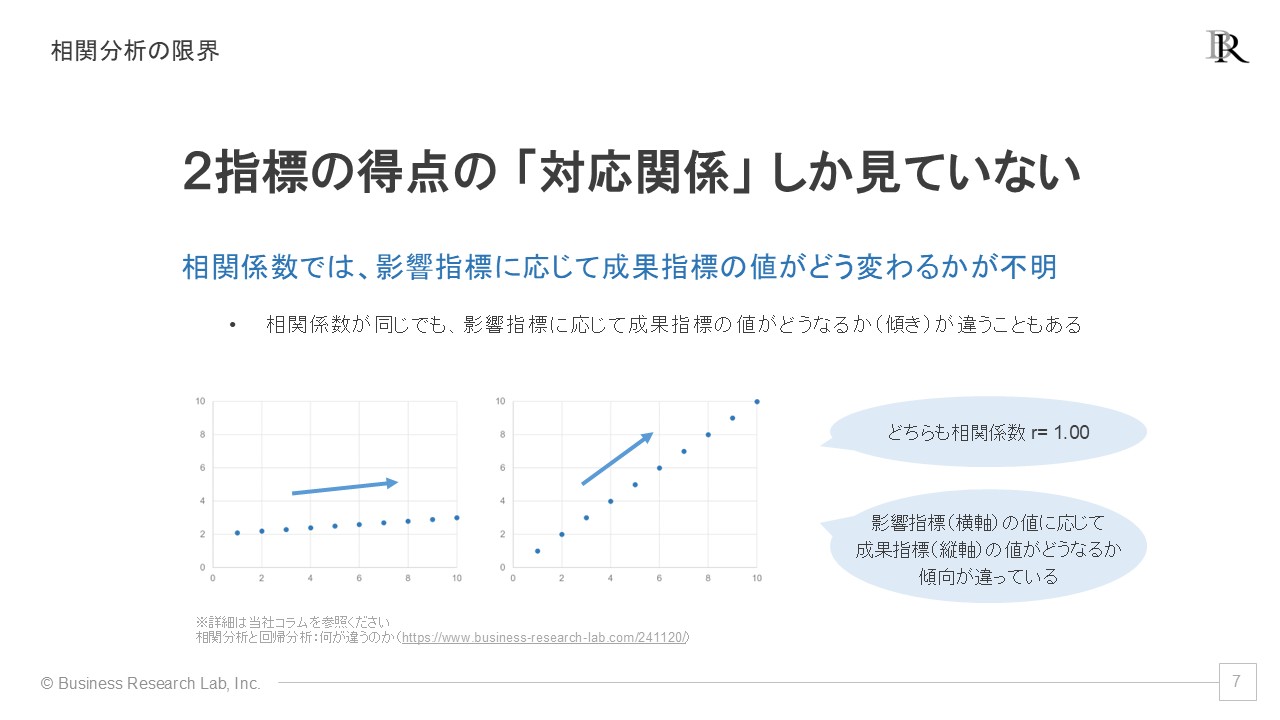
ただし、相関分析には限界があります。具体的には、相関分析は2指標間の対応関係の強さを示すだけで、影響指標の値と成果指標の値が具体的にどう関連しているのかを把握できません。つまり、影響指標の値が高まることに応じて成果指標がどの程度違ってくるのか、相関分析ではわからないのです。

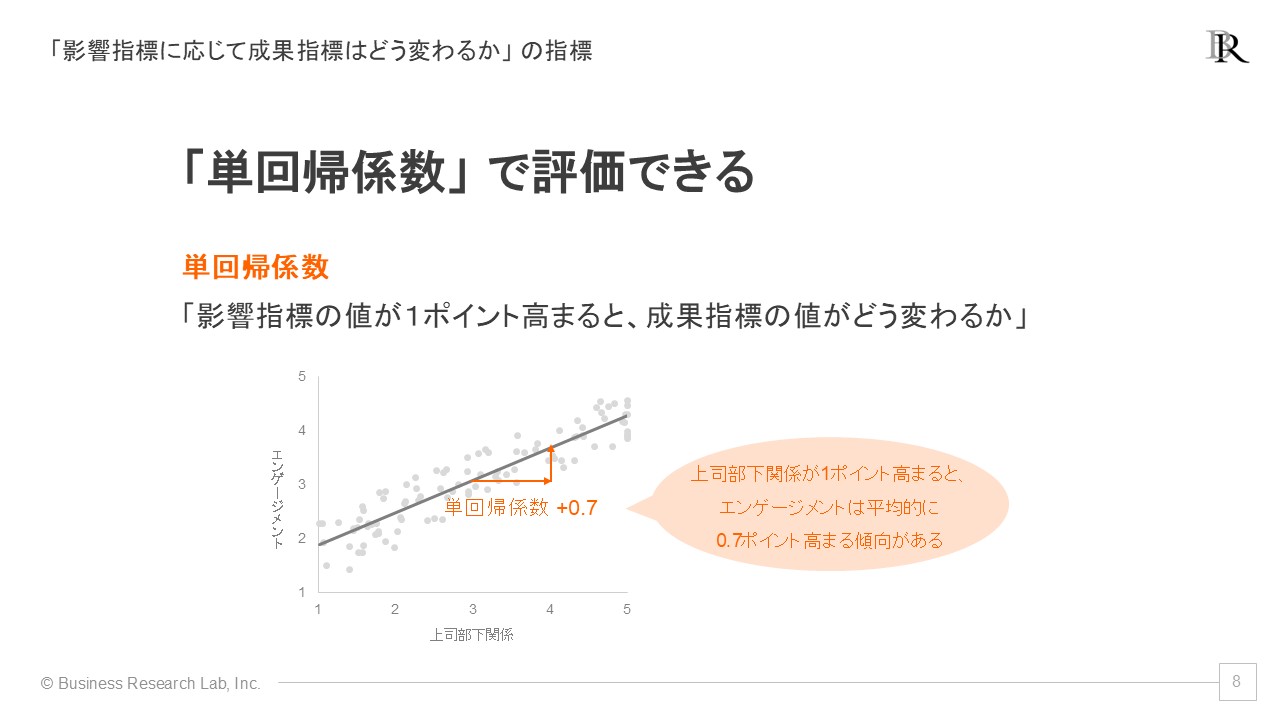
この問題を解決するために用いられるのが回帰分析です。回帰分析は、「影響指標が高まることに応じて、成果指標が具体的にどの程度変化するのか」を評価する分析です。その具体的な数値を示す指標が「単回帰係数」です。例えば、単回帰係数が+0.7であれば、影響指標が1ポイント高まると成果指標が平均して0.7ポイント高まる傾向があることを意味します。

また、この単回帰係数は統計的に有意かどうかを検証することも可能です。これは推測統計の帰無仮説検定の枠組みを使ったもので、実際に測定していない回答者を含む全従業員（母集団）に対しても同様の結果が期待できるのかを検証します。つまり、回帰分析で示された結果が従業員全体に適用できるかどうかの判断材料を得ることができます。

一方で、単回帰係数には影響力の相対的な比較ができないという欠点もあります。例えば、上司部下関係とストレッチ目標を影響指標、エンゲージメントを成果指標として回帰分析を行えば各影響指標で単回帰係数が算出されますが、「どちらがエンゲージメントに対してより強い影響を与えるか」というような比較はできません。

重回帰分析とは

続けて、重回帰分析について解説します。重回帰分析は、単回帰分析とは異なる観点で影響指標と成果指標の関連性を検証し、それによって先ほど挙げた単回帰分析の問題を解消している分析です。

重回帰分析の大きな特徴として、複数の影響指標を同時に分析し、その影響力を比較できるという点が挙げられます。単回帰分析では、一つの成果指標に対して一つの影響指標の関連性しか検証できず、それぞれの影響指標間の影響力の比較はできませんでしたが、重回帰分析ではそれが可能となります。具体的には、成果指標に対して複数の影響指標を同時に設定し、これらの影響指標の影響力を同時に評価します。

重回帰分析を行うと、その代表的な出力として「決定係数」と「標準化偏回帰係数」の2指標が出力されます。

決定係数とは、成果指標が影響指標全体からどの程度影響を受けているのかを総合的に捉える指標です。ひとつひとつの影響指標と成果指標の影響の強さでなく、影響指標全体での影響の大きさを捉えている点が特徴の指標です。決定係数の値には一般的な基準があり、例えば.13以上であれば一定の影響があるとされ、.26以上であれば十分な影響があると判断されます。また、この決定係数は統計的に有意であるかの検証も可能で、有意であれば今回測定していない従業員全体にもこの結果が広く当てはまるだろうと推測できます。

次に、標準化偏回帰係数は、成果指標に対して各影響指標がそれぞれどの程度影響しているかを評価する数値です。この指標は-1.00から+1.00の範囲をとり、数値が1に近いほど影響力が強いことを表します。また、この指標も統計的に有意か否かの検証ができ、標準化偏回帰係数が有意な影響指標は、従業員全体でもその影響指標による影響がありそうだと解釈できます。なお、標準化偏回帰係数は影響力を比較するための指標であり、単回帰係数のように各影響指標と成果指標の値の具体的な対応は検証できません。

この標準化偏回帰係数は、その値の大きさで影響力を比較することが可能な特長があります。例えば上の図のように、エンゲージメントを成果指標として、「上司部下関係」「ストレッチ目標」「競争風土」という三つの影響指標を取り上げて重回帰分析を行ってここで示された標準化偏回帰係数が示されたとしましょう。

標準化偏回帰係数の絶対値は影響力の大きさを表すため、絶対値が最も大きい指標が最も影響力が強いことになります。この例では、まず上司部下関係は統計的に有意であり、従業員全体でもこの指標の影響力がありそうだと考えられます。また、上司部下関係の標準化偏回帰係数は.35でもっとも値が大きく、取り上げた指標の中では一番大きな影響力を持っていそうだと判断できます。

それについて、標準化偏回帰係数が.21で有意だと示されているストレッチ目標は、この指標も従業員全体で影響が見られそうだと考えられると同時に、２番目に影響力の強い指標だと考えられます。一方、競争風土は統計的に有意ではなく、競争風土は従業員全体で影響力を持っていなさそうだと捉えられるわけです。

こうした分析結果は、成果指標の改善に向けた具体的な対策を立てる際にも役立ちます。先の分析結果例では、「エンゲージメントを高めたい場合、最も影響力が強い上司部下関係にまず注力し、その次に影響が見込まれるストレッチ目標の設定に取り組む」というように、影響力に応じて優先順位をつけた具体的な施策を立案することが可能となります。

以上のように、重回帰分析は、影響指標間の影響力を相対的に比較評価できる分析手法として、実務におけるデータ活用の幅を大きく広げるものとなっています

回帰分析の注意点

最後に、回帰分析の注意点を2つ述べます。

1つ目は、回帰分析だけで因果関係を実証することはできないということです。ここまでの解説ではわかりやすさを重視して「影響」と因果関係を表す語句を用いていましたが、厳密には回帰分析のみで因果関係を実証できるわけではありません。統計的には、回帰分析は「影響指標が成果指標に影響を与える」という原因と結果の位置づけを想定して関連性を検証しており、因果関係そのものを実証する分析ではありません。

実際に因果関係をできる限り実証するには、サーベイで取り上げられていない他の影響指標の可能性を考慮した分析や、パネル調査のような複数回の測定を含むサーベイ設計を行う必要があります。そのため、回帰分析の結果だけで因果関係を断定しないよう注意が必要です[6]。

2つ目の注意点は、重回帰分析において影響指標間の相関係数が大きいときに生じる問題についてです。重回帰分析で用いる影響指標同士が強く相関している場合、分析結果が不安定になり、不正確な回帰係数が算出される可能性が高まります。これは「多重共線性」と呼ばれる現象で、標準化偏回帰係数の計算が正確に行われなくなり、影響力の評価が誤る可能性が高まります。

このリスクを回避するためには、重回帰分析に含める影響指標は、互いの相関があまり強くないものを選ぶことが推奨されます。一般的な目安としては、相関係数が0.70を超えない程度の指標を選ぶことが望ましいとされています。

これらの注意点を踏まえて、適切な指標選定や結果の解釈を行うことが、回帰分析を実務に効果的に活用するために重要となります。

Q&A

Q1: 推測統計の結果を転用するために「サンプルが同質か」をどう判断するとよいですか？

黒住：

ひとつには、サンプルの属性を確認することです。例えば、新卒採用者のデータを分析する場合、「新卒」という共通の特徴があるため、年齢層やキャリアのスタート時期が似ていることが考えられます。このように、分析対象の属性が似ている場合、結果を他のサンプルにも適用できる可能性が高いです。一方で、新卒と中途採用者を比較する場合は、属性が異なるため、結果をそのまま適用するのは難しいかもしれません。

能渡：

言い換えると、分析自体で同質性を保証することは難しいため、サンプル収集時の段階で注意を払う必要があります。例えば、若手のみや回答に積極的な人など、特定の層に回答者が偏らないようにサーベイを設計し、全体の属性を確認することが大切です。得られたデータに偏りがあると、そのデータを基にした推測も偏る可能性が高くなります。

Q2: 「選抜効果」について人事の場面で具体例を教えてください。

黒住：

例えば、「満足度調査」では選抜効果が起きるリスクがあります。満足度調査では、回答するのが「非常に満足している人」か「非常に不満を感じている人」に偏ることがあります。その結果、回答者が特定の層に集中し、本来は存在している「満足度」と想定していた要因との相関が弱く見えてしまう可能性があります。

能渡：

選抜効果を防ぐのにも、組織全体からバランスよく回答を集めることが重要です。ただし、回答を強制することは、回答に忖度が働いて正直な回答が得られなくなる可能性を高めることにつながるため、避けてください。

回答者の協力を得るためには、普段から信頼関係を構築し、アンケートの結果がうまく活用されることを伝えることが効果的です。例えば、アンケートをもとに職場環境が改善された事例を共有するなど、回答することで得られるメリットを実感してもらうことが重要といえます。

脚注

[1] 統計的な解説は、当社の右記のコラムを参照ください；人事のためのデータ分析講座 相関分析 ~2つの指標の関連を検証する~（セミナーレポート）

[2] 相関係数は、一の位の「0」を省略し、小数点第１位から表記する通例があります。

[3] 両者の違いについては、当社の右記のコラムも参考になります；相関分析と回帰分析：何が違うのか

[4] 推測統計の詳細は当社の右記のコラムを参照ください；人事のためのデータ分析講座「統計的に有意」を学ぶ（セミナーレポート） 

[5] これは「統制」と呼ばれる手法の一部です。詳細は、当社の右記のコラムを参照ください；統制とは何か

[6] 詳しくは、当社コラム「因果関係とは何か？相関系との違い・検証方法」で解説しています。

---

登壇者

能渡 真澄　株式会社ビジネスリサーチラボ チーフフェロー

信州大学人文学部卒業、信州大学大学院人文科学研究科修士課程修了。修士（文学）。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を、他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており、通常では捉えることが困難な、様々なデータの背後にある特徴や関係性を分析・可視化し、その実態を把握する支援を行っている。

黒住 嶺　株式会社ビジネスリサーチラボ フェロー

学習院大学文学部卒業、学習院大学人文科学研究科修士課程修了、筑波大学人間総合科学研究科心理学専攻博士後期課程満期退学。修士（心理学）。日常生活の素朴な疑問や誰しも経験しうる悩みを、学術的なアプローチで検証・解決することに関心があり、自身も幼少期から苦悩してきた先延ばしに関する研究を実施。教育機関やセミナーでの講師、ベンチャー企業でのインターンなどを通し、学術的な視点と現場や当事者の視点の行き来を志向・実践。その経験を活かし、多くの当事者との接点となりうる組織・人事の課題への実効的なアプローチを探求している。