2025年4月9日
組織の実態を捉えるデータ整理のエッセンス:集計・可視化の技法(セミナーレポート)
ビジネスリサーチラボは、2024年10月にセミナー「組織の実態を捉えるデータ整理のエッセンス:集計・可視化の技法」を開催しました。
近年、人事部門やマネジメントの現場では、データに基づいた意思決定の機会が増えています。社員のパフォーマンス評価や組織全体の状況把握など、実態を正確に把握し、データを適切に読み解き、伝えることが求められています。
しかし、日常的に扱っているデータでも、その処理に自信を持てないまま進めてしまうことはないでしょうか。自信なく曖昧な理解のままでデータを集計・分析し続けると、重要な課題を見逃し、チームや組織の実態を捉え損ねてしまいます。
本セミナーでは、データの基本的な集計・可視化について考え方と処理方法を解説し、実務に役立つデータ活用法を紹介しました。
※本レポートはセミナーの内容を基に編集・再構成したものです。
平均値だけを見る危険性
仮想例1:エンゲージメントサーベイの部署間比較
黒住:
まず、「平均値だけを見ることの危険性」について説明します。仮想の例として、エンゲージメント・サーベイを行ったと想定して話を進めます。
ある企業がエンゲージメント・サーベイを実施し、部署Aと部署Bの結果を比較したとしましょう。そして、平均点と標準偏差が次のような結果だとします。
- 部署A:平均点0点(5点満点)、標準偏差0.53
- 部署B:平均点9点(5点満点)、標準偏差1.08
平均点だけを見ると、両部署は似通っているように思えます。しかし、よくみると標準偏差の大きさが異なります。ここで、上記の仮想データについて、ヒストグラムを使って回答の分布を確認してみます。
部署Aは3点前後に集中しているのに対し、部署Bは1点から5点まで広く分布していることがわかります。言い換えると、部署Bではエンゲージメントが非常に低い人も高い人もおり、個人差が大きいということです。そのため、もし平均点だけを見ていた場合、こうした個人差に違いがあるという実態を見落としてしまうリスクがあります。
この仮想例から学べる教訓として、データを読む際は複数の指標を確認することが重要です。そもそもアンケート調査を実施する状況、そして、その集計結果を元に考察する状況とは、回答者が多く、個別の回答よりも回答全体の傾向を見たいという目的が多いでしょう。しかし、集計結果の一部しか見ていないと、全体像を誤解する危険があります。そこで、集計結果を確認するときは、平均値に加えて他の指標も含めて総合的に評価することが大切です。
では、具体的に何を確認すればよいのかについて、整理していきたいと思います。指標は主に二つのカテゴリーに分けられます。一つ目が「代表値」です。代表値には平均値が含まれますが、これは測定した項目や指標のデータ全体を一つの値で表すための指標の総称です。もう一つが「散布度」です。散布度とは、データの広がりやばらつきの程度を示す指標です。以降では、それぞれの具体的な指標について見ていきましょう。
代表値の解釈と活用
まず「代表値」としてよく使われるのは、平均値、最頻値、中央値の三つです。定義的な説明から始めますが、平均値は、全ての回答の合計を回答数で割った値です。中央値は、回答を大きさ順に並べたときにちょうど真ん中の順位になる値です。最頻値は、データの中で最も頻繁に出現した値です。
では、それぞれの指標はどのように解釈できるかを考えてみます。先ほどの部署Aの仮想データと併せてみます。
まず平均値は、個人差をならすことによって、ばらつきよりもデータ全体の傾向を示していると解釈できます。対して中央値は、個人差を考慮したうえで、真ん中に当たる値を知るのに役立ちます。ばらつきが大きいデータでも中央値を確認することで、データの中心がわかります。最頻値も、個人差を踏まえた上で、最もよく現れる値だといえます。このように考えると、三つの代表値それぞれが異なる角度からデータを捉える手がかりになることがわかります。
さらに、これらの代表値の解釈が、実務的にどう活用できるのかについて例を紹介します。たとえば、先ほどの仮想例で部署Aと部署Bのデータを確認してみます。
平均値では、両方とも約3点で、全体的な傾向としては、あまり差がないと思えます。次に、中央値を見てみると、データの中心が満点の半分である2.5点以上に位置していることがわかり、全体の傾向としては、何方もある程度高いエンゲージメントを持つ回答者が多いことが示されます。
また、最頻値については、特に部署Bで独自の特徴が表れています。先ほど紹介したように、部署Bは個人差が大きい状況でしたが、最も多かった回答は3点前後となっています。これにより、確かに回答のばらつきは大きいけれど、平均点に近い回答が最も多いのだということが見えてきます。このように、代表値を多角的に確認することで、データの実態をより的確に捉えることが可能になります。
散布度の解釈と活用
続いて、「散布度」について説明します。散布度にはいろいろな指標がありますが、特に代表的なのが「標準偏差」です。ここでは数式としての説明省き、その意味をお伝えします[1]。標準偏差は、平均値を基準にして、各回答がどの程度ばらついているかを示す指標です。つまり、全体の個人差の大きさを示すものです。
標準偏差には便利な特徴があり、個人差の大きさを直感的に捉えることができます。便利な特徴とは、データが正規分布している場合、平均値から標準偏差1つ分の範囲に約7割、標準偏差2つ分の範囲に約9割の回答が収まるというものです。先ほどの仮想データから、部署Aのデータを使って図で確認してみましょう。
例えば、平均値が3の場合、標準偏差が1つ分だと範囲は2.47から3.53になり、この範囲に約7割の回答が含まれるということです。さらに、標準偏差2つ分の範囲は1.94から4.06になり、こちらの範囲には約9割の回答が収まります。このように、標準偏差を平均値と併せて確認することで、データの散らばり具合を大まかに把握できるのです。
では、この標準偏差が実務でどのように活用できるかというと、意思決定に活用することができます。引き続き、エンゲージメントの得点を例にして考えてみましょう。
まずは、エンゲージメントの平均点が高い場合です。このとき、もし個人差が小さければ、全体的に優れていると確認でき、介入の優先度が低いと判断することができます。一方で、個人差が大きい場合は、注意が必要です。つまり、全体としては優れた結果でも、低い得点の人がいる可能性があるため、低い得点の人に対してはフォローが必要だと判断することができます。
逆に、エンゲージメントの平均得点が低い場合について考えてみます。もし、個人差が大きい場合は、回答者の中にはエンゲージメントが高い人も含まれている可能性があるため、特に低い得点の人にむけ、個別対策のアプローチが効果的だと判断できます。
また、エンゲージメントの平均得点が低く、かつ、個人差も小さい場合は、部署全体に対して一律の改善策を講じるのが有効です。全員が同様に低い傾向にあるため、介入の優先度が高い群、あるいは、対策によって成果が得られる見込みが高い群と判断できるのです。
このように、平均点に加え個人差の大きさも併せて考慮することで、意思決定がより深い視点から可能になります。逆に、全体の傾向を把握する際、例えば平均値にだけ頼ると、実態を見誤るリスクがあります。つまり、複数の指標が存在することを理解し、目的に応じてそれらを適切に組み合わせて活用するような、多角的な視点を持つことが重要なのです。
データの特徴を考慮しない危険性
仮想例2:同僚のサポート頻度の評価
2つ目のテーマとして、「データの特徴を考慮しないことによる危険性」についてお話しします。ここでは、「同僚のサポート頻度を測定したケース」を仮想例として取り上げます。
組織のサーベイを使って、現在の部署内でどれくらい同僚間の助け合いが行われているかを調査したとします。その対象となった部署Cでは、アンケートの集計結果として次の結果だったとしましょう。
- 部署C:平均点9点(5点満点)、標準偏差1.08
5点満点中の3.9点、中間よりも高得点よりに思えます。また、標準偏差が1.08であれば、データのばらつきもそれほど大きくはないと考えられます。つまり、個人差を踏まえたうえでも、サポート頻度が高めである望ましい部署だと、この結果から判断できそうです。
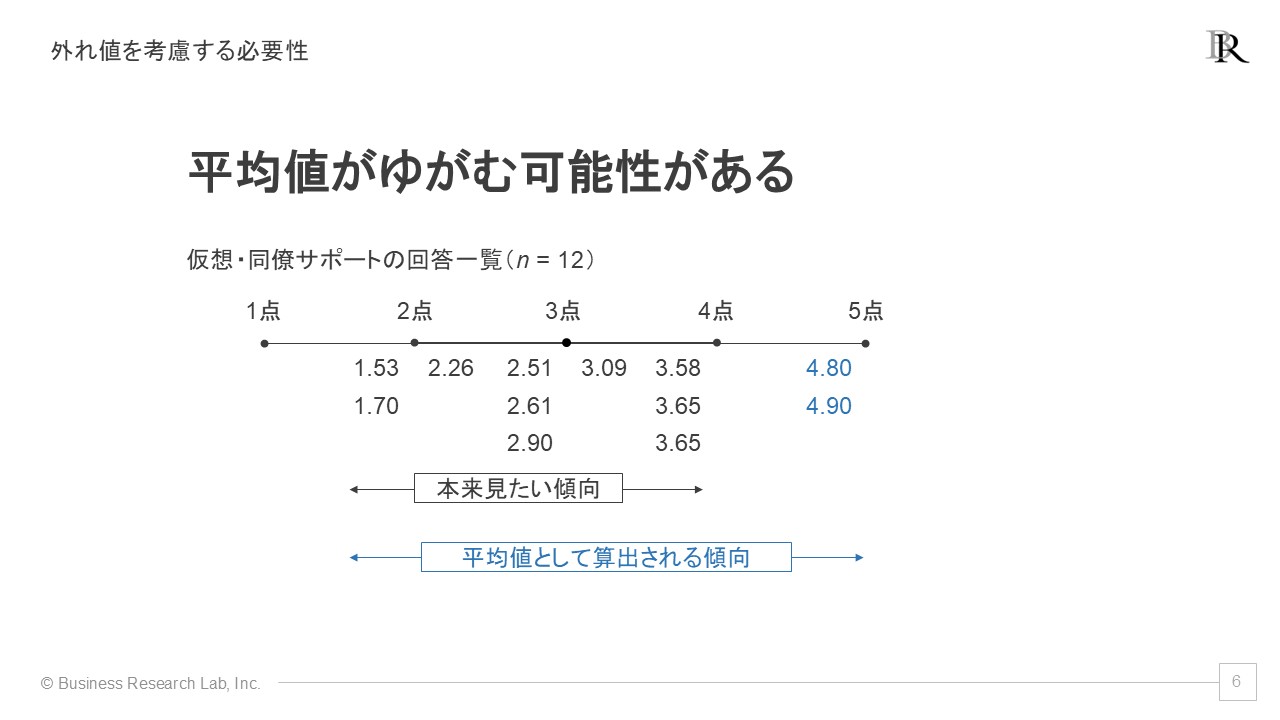
しかし、ここで仮想のローデータを確認してみます。上記の部署Cの回答が、次の図のようになっていたとしましょう。
回答を並べてみると、その中には4.8点や4.9点という、ほぼ満点に近い評価を出している人が2人含まれているのが分かります。一方で、他の人たちの評価は2点台から3点台に留まっています。つまり、平均3.9点という結果は、サポートに積極的な2人が引き上げた得点であり、その他のメンバーのサポート頻度はそれほど高くないという実態が見えてきます。
このように、一部の高い評価に引っ張られて全体の平均点が上がるケースは、データの分析における注意点の一つです。ここから見える教訓は、調査の結果に特殊な回答傾向が表れる可能性を想定する必要がある、ということです。以降では、そうした特殊な回答傾向の代表例を紹介します。
外れ値とその対処
特殊な回答傾向の1つとして、「外れ値」という事例について紹介します。これは、先ほどの例にもあったような、他の回答に比べて大きく異なる値を指します。例えば、他の値と比べて非常に大きかったり、逆に非常に小さかったりする値が該当します。
なぜ外れ値を考慮すべきかというと、平均値が歪む可能性がある点が挙げられます。このことをイメージしてもらうため、再び先ほどの部署Cの仮想例と併せて示します。
先ほどの例でみると、実際に全体像を把握したいのは、ほとんどの回答が含まれている1.5点から4点以内の程度に収まっている部分だと言えます。しかし、平均点を算出する場合は外れ値も含んでしまうため、本来の傾向よりも歪んだ傾向を捉えていることがわかるかと思います。このように、外れ値があると、平均値が実態を反映しない歪んだ結果になる恐れがあるのです。
実際にどのように影響が出るか、計算した結果を見てみましょう。上記の例のうち、先ほども示した全員での結果と、高得点の2人、つまり外れ値を取り除いた結果は以下のようになります。
- 外れ値を含んだ場合:平均 09 (標準偏差 1.07)
- 外れ値を除いた場合:平均 74 (標準偏差 0.77)
このように外れ値が集計に与える影響は大きく、誤解を招く可能性があるため、注意が必要です。また、サンプル数が少ない場合には外れ値の影響がさらに大きくなることもあります。
こうした外れ値に対処する方法として、代表的なものは2つあります。まず1つ目が「中央値の確認」です。中央値は、データを小さい順に並べたときの中央の値で、外れ値の影響を受けにくいという特徴があります。中央値を見ることで、外れ値に引っ張られない中心的な傾向を確認できます。
2つ目は「トリム平均」の算出です。これは、外れ値を除外した上で平均値を計算する方法です。例えば、全体の上位と下位から数%ずつを除外して平均を算出する方法です。このように特定の割合を定めて外れ値を除き、より実態に即した平均値を得ることができます。
ただし、外れ値の処理には注意が必要です。外れ値を安易に除外すると、データの一部を恣意的に改変するリスクが生じます。高い点数や低い点数が単なる外れ値なのか、実際にそのような傾向があるのかを慎重に判断する必要があります。外れ値と見なす基準を明確にし、データの客観性を保つ意識が重要です。
非正規分布とその対処
特殊な回答傾向のもう一つのポイントが、「非正規分布」です。非正規分布とは、正規分布ではない分布の総称となりますので、まず正規分布について簡単に触れます。たとえば、大規模な従業員調査や全国規模のアンケートなどのデータは、通常「中間的な値」が多く、大きい値や小さい値に向けて回答数が少ない傾向があります。このようにデータの中央に多くの値が集まり、両端に向かって数が少なくなる形を「正規分布」と呼びます。
一方、そうした正規分布でないものが、非正規分布です。非正規分布にはいくつかの種類があり、調査の内容や規模によって異なる形が現れることがあります。たとえば、「中間層が減少し低所得者層と高所得者層に分かれる」という回答数の山が2つ現れる分布です。あるいは、昇進や表彰の経験など、頻度が少ない特別な出来事は、経験していないあるいは少ない方が多数派で、複数回経験している人が少ないながらも存在するという形で、分布の右側が伸びた形になることもあります。
非正規分布を考慮すべき理由は、集計データだけではこうした偏りに気づきにくい点にあります。たとえば厚生労働省の調査結果では、2023年の日本の平均所得が524万円、中央値が400万円というデータがあります[2]。この集計結果だけを見ると、平均値が中央値より高いという点でやや偏りがあるとわかりますが、「全体的には比率が少ない高所得者が存在している」という全体の分布の形まではわかりにくいのです。
そうした非正規分布になっている可能性を考慮し、気づくためには、データの可視化が非常に重要です。偏りや非正規分布に気づくための最も簡便な方法は、グラフでデータを可視化することです。これにより、平均値や中央値だけでは見逃しがちな分布の特徴が視覚的に捉えられます。正規分布でない特異な形状や傾向があれば、グラフで確認することで見落としを防ぐことができます。
実践時のポイント
最後に、これまでのポイントを踏まえ、自分で実際にデータの集計結果を扱う、あるいは読み取るときに注意すると良いポイントや進め方をまとめます。今回は大きく三つのポイントに分けて紹介します。
一つ目は、「データの種類と対象を考慮しておく」という点です。これは、データから実態を誤って解釈するリスクをあらかじめ想定するということです。たとえば、「ハイパフォーマーが含まれているので外れ値とみるべきかもしれない」「分布が偏りそうな内容だから集計の可視化を計画に組み込んでおこう」といった対応により、実態を誤解するリスクへ事前に抑えることができます。
二つ目のポイントは「平均値と標準偏差を確認する」という点です。本日も見ていただいたように、全体の傾向を把握する際には、平均値だけでなく標準偏差も確認し、データに個人差がある場合はその範囲も考慮します。平均値で全体の傾向を掴むだけでなく、標準偏差によって個人差の幅を確認し、それを考慮に入れてデータを評価することで、より実態に即した理解が可能となります。
最後のポイントは「データの特異性を確認する」という点です。平均と標準偏差から読み取った傾向に誤解がないか、特異なデータがないかを、別の指標によって精査するということです。たとえば、平均値と中央値が大きく異なる場合は、外れ値の存在が考えられますし、可視化を組み合わせることで特異な分にも気づくことができます。このように、さまざまな指標を活用し、多角的な視点でデータを評価することで、データの実態をより正確に把握することができます。
グラフに盛り込める有用な情報とは
能渡:
続けて、ここからは集計した情報をどのようにグラフで示すと良いかについて解説していきます。多くの方が集計データをグラフで表現することに取り組んでいるかと思いますが、実際にはグラフの示し方によっては、いくつかの問題が生じることがあります。
その問題とは、たとえば有用な情報が十分に見えなくなってしまったり、示し方によってグラフを読む人が誤解してしまう恐れがあるといった点です。こうした懸念を避けるために、実態を正確に把握しやすいグラフの作成方法についてお話ししていきます。本日は特に、ある指標を集計して平均をとった得点データを棒グラフで示す手法について解説していきます。
最初にお伝えするのは、どういった情報を盛り込むと有用なグラフになるのかです。集計データをグラフ化する際、より有用な情報を伝えるための工夫が存在しますが、その工夫自体はあまり知られていません。その結果、少し物足りない、もったいないと感じてしまうようなグラフが作られがちです。
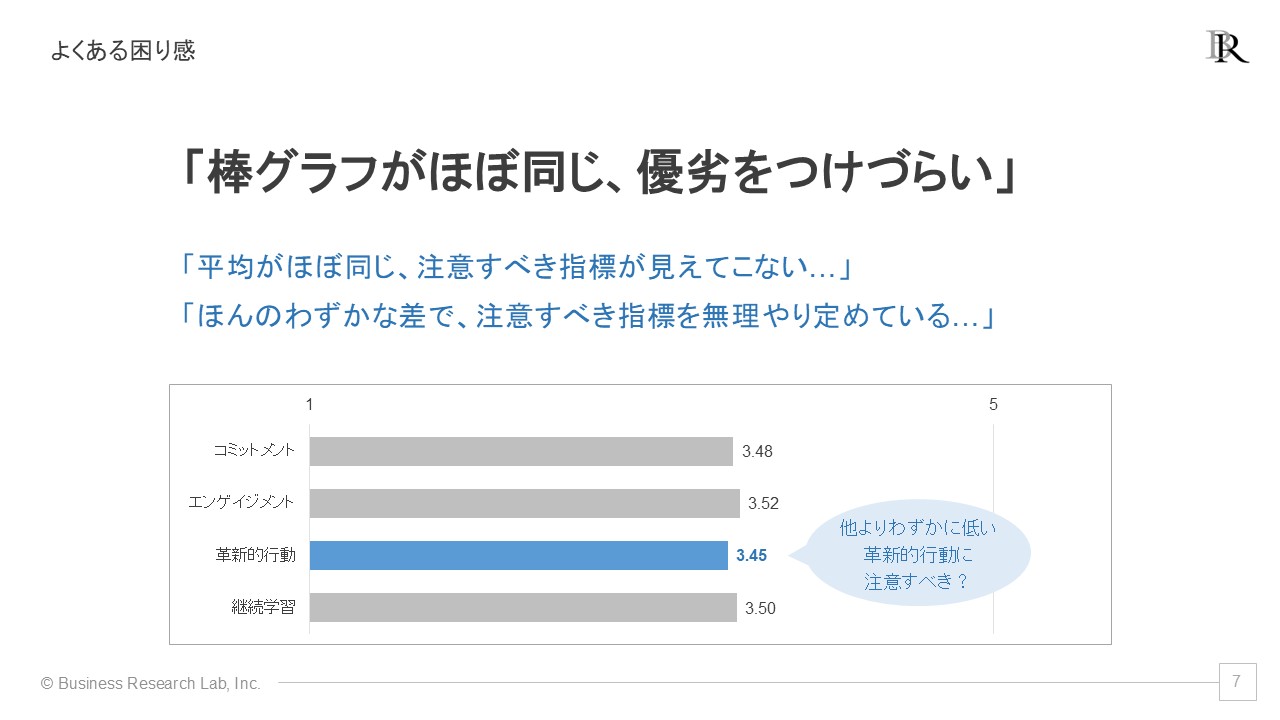
まずは、よくある集計データのグラフ化とそこに感じる困り感について架空例を示します。ここでは、あるサーベイで得られたコミットメント、エンゲージメント、革新的行動、継続学習など、さまざまな指標について回答の平均を集計してグラフ化するとします。
よく見るグラフのひとつが棒グラフですが、様々な指標の平均などを取ってその得点を棒グラフにして並べ、見た目に比較できるよう図示することが多いでしょう。そして、こういった結果の中でよく耳にする困り感が、「グラフを並べてもだいたい同じような得点に見えてしまい、違いが見えてこない」ことです。
この例では革新的行動が少し低い得点になってはいますが、それを注意すべき指標とみなしてよいのか迷ってしまいます。「わずかに平均値が低い指標を取り上げて『注意すべき指標だ』と無理矢理設定することは、本当に妥当なのか」と悩んでしまうわけです。せっかくグラフで結果を示しても、ここから有効な打ち手や対応策は見えてきません。
本日の狙いは、このグラフに更なる追加情報を盛り込んで考えることで、「注意すべき、対策すべき指標を見抜く」技法を身につけていただくことにあります。先ほどの黒住さんの解説パートを振り返ってみると、さまざまな統計指標を参照することで、より良い理解に繋げていこうというお話がありました。平均以外の統計指標も参照すれば、より正確な実態把握につながります。
グラフにおけるデータ可視化の技法
続けて、ここからは集計した情報をどのようにグラフで示すと良いかについて解説していきます。多くの方が集計データをグラフで表現することに取り組んでいるかと思いますが、実際にはグラフの示し方によっては、いくつかの問題が生じることがあります。
一般的な棒グラフは得点の比較が主な目的で作成されていますが、それだけでは主に平均などの得点しか示されず、情報が限定的です。特に、得点が似通った項目同士の重要性や優先順位を明確にするのが難しく、非常に近い得点が並んでいる場合、どの項目を優先すべきか判断に困るという課題があります。
そこで重要となるのが、データの具体的な分布を示すことができるグラフ化の技術です。得点情報に加えてデータの分布も見ることで、各データの特徴をより正確に把握することができます。加えて、先ほどの黒住さんの話にもありました、外れ値や非正規分布の問題に気づくことにもつながります。
データ分布を直接示すグラフ化
最初に、データの分布も示す代表的なグラフの示し方として、「ビースウォームプロット」と「バイオリンプロット」を紹介します。
「ビースウォームプロット」は蜂(ビー)の群れ(スウォーム)のようにひとつひとつのデータをグラフ上に示す方法です。各得点層にどれだけ回答者がいるかを個々の点で表現し、回答者が集中している得点層を一目で捉えやすくなります。
一方、「バイオリンプロット」は回答者数が多い得点層を曲線の幅を広く、少ない得点層を曲線の幅を狭く示し、どの得点に回答者が集中しているかを視覚的に分かりやすくします。これらのグラフを活用することで、外れ値や偏った回答の分布を明確に把握することが可能になります。
これらのグラフ化を用いるメリットは、対策の打ちどころや方法を考えやすいことです。架空例で確認してみましょう。
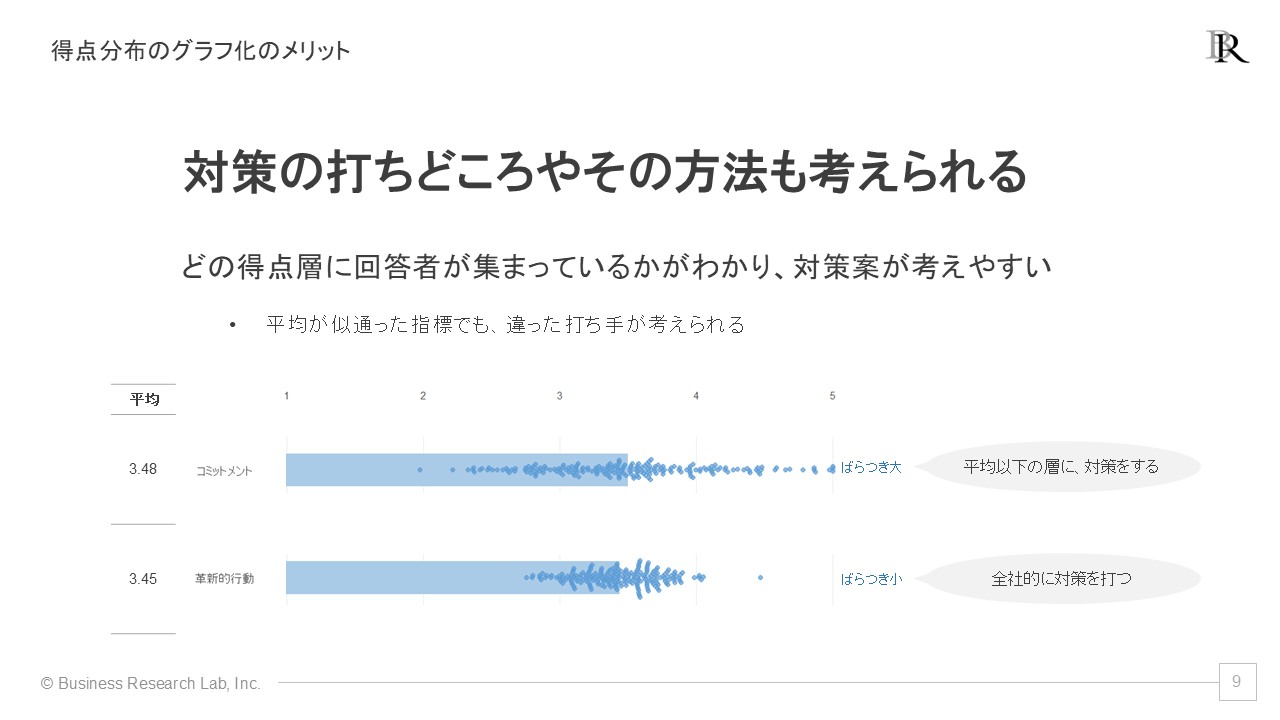
この例では、サーベイで得られたコミットメントと革新的行動のデータについて、ビースウォームプロットで示しています。2つの指標の平均は3.48, 3.45とほぼ違いがないですが、得点分布には大きな違いがあります。
コミットメントは、平均付近に多くの人が集まりつつ、低い得点層にも高い得点層にも人がまばらにいて、ばらつきが大きい状態だとわかります。この結果に対してコミットメントを高める対策をするならば、やはり着手すべきは低得点層でしょう。平均を大きく下回る人が一定数いるため、彼らに重点的対策をする案が浮かんできます。
一方、革新的行動は、平均付近に人が多く集まっており得点が極端に低い・高い人が見られず、ばらつきが小さい状態だとわかります。ここから革新的行動に対する対策を練るならば、全社的な対策を考えるのが有効です。ばらつきが少なく団子状態であるため、得点がとても高い人がおらず、全体的な底上げをしていくべきだと考えられます。
このように、平均が似通った指標でも得点分布も示すグラフ化を用いることで、組織がどの層に対して重点的な対策を打つべきかが具体的にわかり、効果的な施策立案に役立ちます。
加えて、外れ値や非正規分布についても、下の図のように確認することができるメリットもあります。得点分布を確認することで、単純な得点の高さに留まらない様々な情報を得ることができるのです。
なお、ビースウォームプロットやバイオリンプロットを作ることが難しい場合は、度数分布やヒストグラムを見るのも手です。度数分布やヒストグラムも測定されたデータの分布を示すため、同等の情報を把握できます。
標準偏差と中央値の表示・確認
次に、標準偏差や中央値などの指標をグラフと共に示すことも有効です。これらの指標をグラフに追加することで、データのばらつきや分布の偏りを大まかに把握することができます。
標準偏差とは、「データが平均の周辺でどれくらいばらついているか」を示す指標です。これを見ることで、データのばらつきが大きいかどうかを直感的に評価できます。例えば、標準偏差が非常に小さい場合、データは平均付近に集中していることが分かります。一方、標準偏差が大きい場合は、回答が広範囲に散らばっていることが推測できます。
黒住さんによる散布度の解説にて「データが正規分布している場合、平均値から標準偏差1つ分の範囲に約7割、標準偏差2つ分の範囲に約9割の回答が収まる」と述べていました。これを基準にして、標準偏差からデータのばらつきを大まかに想像できるわけです。
また中央値は、「データを並べた時にちょうど真ん中に来る値」を示す代表的な指標です。中央値の特徴として、外れ値に影響されにくいという性質があります。もしデータの分布が歪んでいる場合、平均値と中央値の間にずれが生じやすいため、この二つの指標が大きく異なることで、分布の歪みに気づくことができます。
こうした標準偏差や中央値の情報は、ビースウォームプロットやバイオリンプロットなど、得点分布が直接視覚的に分かるグラフを用いている場合には、必ずしも表示する必要はありません。しかし、棒グラフのみを利用する場合は、これらの指標を追加することで、見えにくい分布状況を把握する助けになります。これらの指標はExcel関数で簡単に出力できるため、まずはここから始めてみるのも良いでしょう。
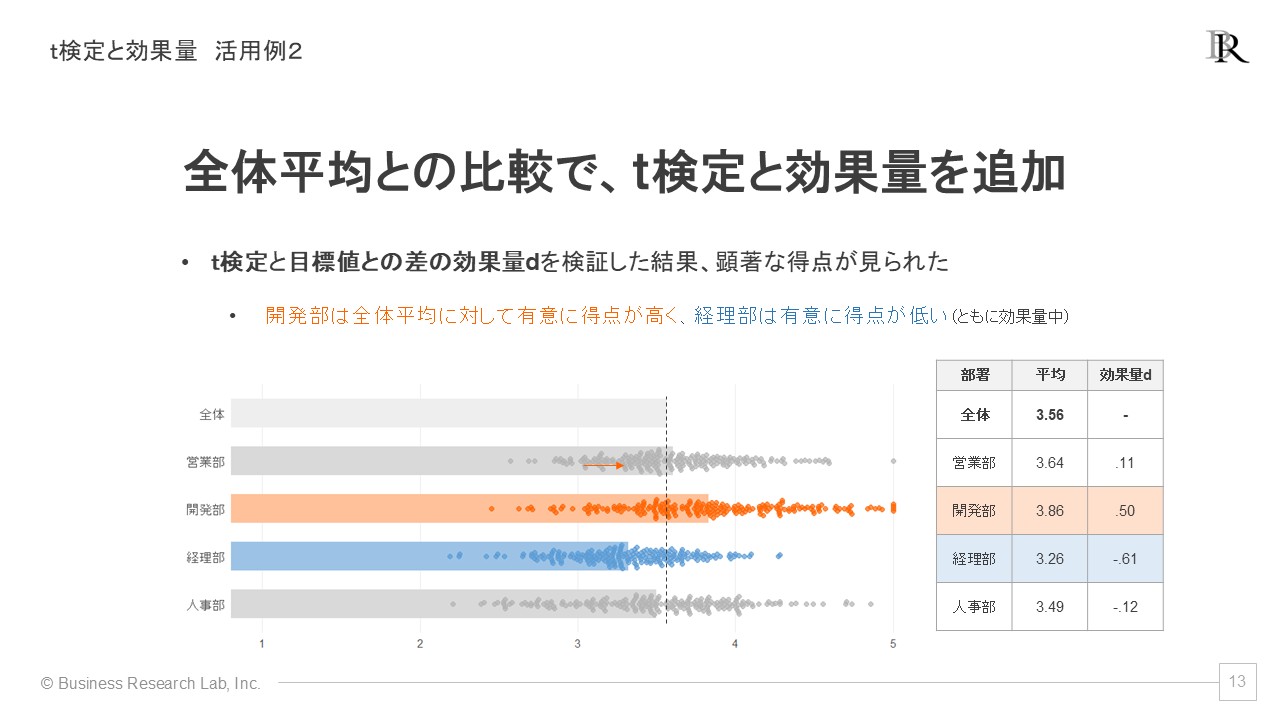
t検定や差の効果量dの活用
最後に、ここまでとはやや異なるアプローチとして、全体平均や事前に設定した基準値と比較して各指標を評価する方法について解説していきます。
例えば、KPIの得点が目標値を超えているかどうか、あるいは部署ごとに得点が全体平均に対してどれくらい高いのかを評価したい場合があります。このような状況では、「t検定」と「差の効果量d」という2つの指標を活用することができます。
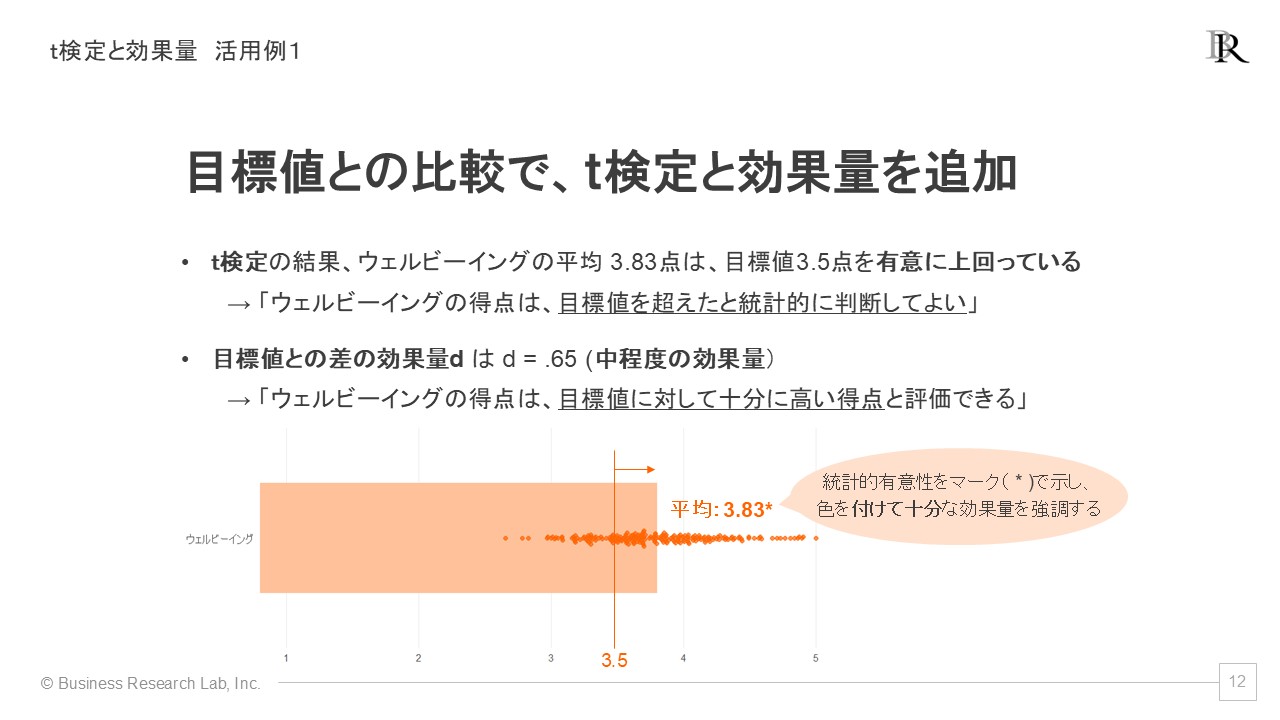
「t検定」とは、2つの得点間で、差が統計的に有意であるかどうかを検証するための分析手法です。これを用いると、サーベイで得られた指標の得点が目標値を超えたと言えるのかをデータのばらつきを加味して判断できます。サーベイの各指標の目標値を3.5点に設定し、実際のサーベイ結果が3.83点だった場合、1標本t検定を行い有意であれば、「この指標は統計的に見て目標値を超えている」と主張する根拠が得られます。
もう一つの指標である「差の効果量d」は、得点差の大きさを評価するための指標です。この指標は単に得点差を示すだけではなく、得点のばらつきを考慮に入れているため、「基準値に対してどの程度大きいのか」を一律化された基準で統計的に判断することが可能です[3]。
これら2つの指標をグラフに追加するメリットは、得点が高いまたは低いことを統計的根拠に基づいて明確に示せることがあります。例えば、ウェルビーイングの得点が目標値を統計的に有意に上回っており、さらに効果量が中程度であるという結果が得られれば、「ウェルビーイングの得点は目標値を十分に超えている」と統計的に評価できます。
さらに、全体平均との比較においてもこのアプローチは有効です。例えば、部署ごとの得点を目標値でなく全体平均と比較し、開発部が全体平均より統計的に有意に高く、経理部が有意に低いという結果を得られれば、明確なエビデンスに基づき、経理部に対してより積極的な対策を講じる必要があることを主張できます。
以上のように、t検定と差の効果量dを用いて基準値や全体平均との比較評価を行うことで、各データの平均の大きさを統計的な裏付けをもって解釈できます。
ここまで解説したように、各指標の集計において単に平均だけ示した棒グラフを示すのは非常にもったいなく、もっと言えば、示されていない分布などの情報から判断を誤る可能性もあります。本日解説した様々なグラフ化の方法を駆使して、より有意義な集計結果の図示と理解を掘り下げていただくのが良いでしょう。
Q&A
Q「実際の回答」ではどの程度歪みが発生するのでしょうか
能渡:
経験則上、データの歪みは割と発生しやすい印象も持っています。特に、質問内容や測定対象によって歪みが大きくなることがあります。例えば、「離職意思」についての質問を直接しても、ほとんどの方が「辞めたい」とは答えないため、回答が低い方に偏りがちです。
しかし、その中でも「辞めたい」と強調して回答する方が少数ながら存在します。このような回答は外れ値に見えるところもあります。このように、指標によっては回答に歪みや偏りが生じやすく、棒グラフや具体的な回答値の分布など実際のデータの広がりを確認することが安全かと思います。
黒住:
他にも、心理学の尺度などでは正規分布に近い形になると期待されていますが、実際の回答データでは現場によって異なる形をとることもあります。例えば、項目の指示内容を、別の意味でとらえるといったケースです。そのため、実際のデータを確認して、現場ごとの「リアル」を捉えることが重要だと考えます。
脚注
[1] 数式としての散布度の解説は、当社の別のコラムで紹介していますので参照ください;散布度とは何か:回答の分布を概観するために
[2] データの詳細は右記をご確認ください;厚生労働省「2023(令和5)年 国民生活基礎調査の概況」
[3] t検定と差の効果量dは、当社コラムでそれぞれ解説しています;
t検定について:「一標本のt検定:人事データ分析の基礎と応用」
差の効果量dについて:「効果量とは何か:「差の大きさ」を評価する指標」
登壇者
 能渡 真澄 株式会社ビジネスリサーチラボ チーフフェロー
能渡 真澄 株式会社ビジネスリサーチラボ チーフフェロー
信州大学人文学部卒業、信州大学大学院人文科学研究科修士課程修了。修士(文学)。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を、他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており、通常では捉えることが困難な、様々なデータの背後にある特徴や関係性を分析・可視化し、その実態を把握する支援を行っている。
 黒住 嶺 株式会社ビジネスリサーチラボ フェロー
黒住 嶺 株式会社ビジネスリサーチラボ フェロー
学習院大学文学部卒業、学習院大学人文科学研究科修士課程修了、筑波大学人間総合科学研究科心理学専攻博士後期課程満期退学。修士(心理学)。日常生活の素朴な疑問や誰しも経験しうる悩みを、学術的なアプローチで検証・解決することに関心があり、自身も幼少期から苦悩してきた先延ばしに関する研究を実施。教育機関やセミナーでの講師、ベンチャー企業でのインターンなどを通し、学術的な視点と現場や当事者の視点の行き来を志向・実践。その経験を活かし、多くの当事者との接点となりうる組織・人事の課題への実効的なアプローチを探求している。