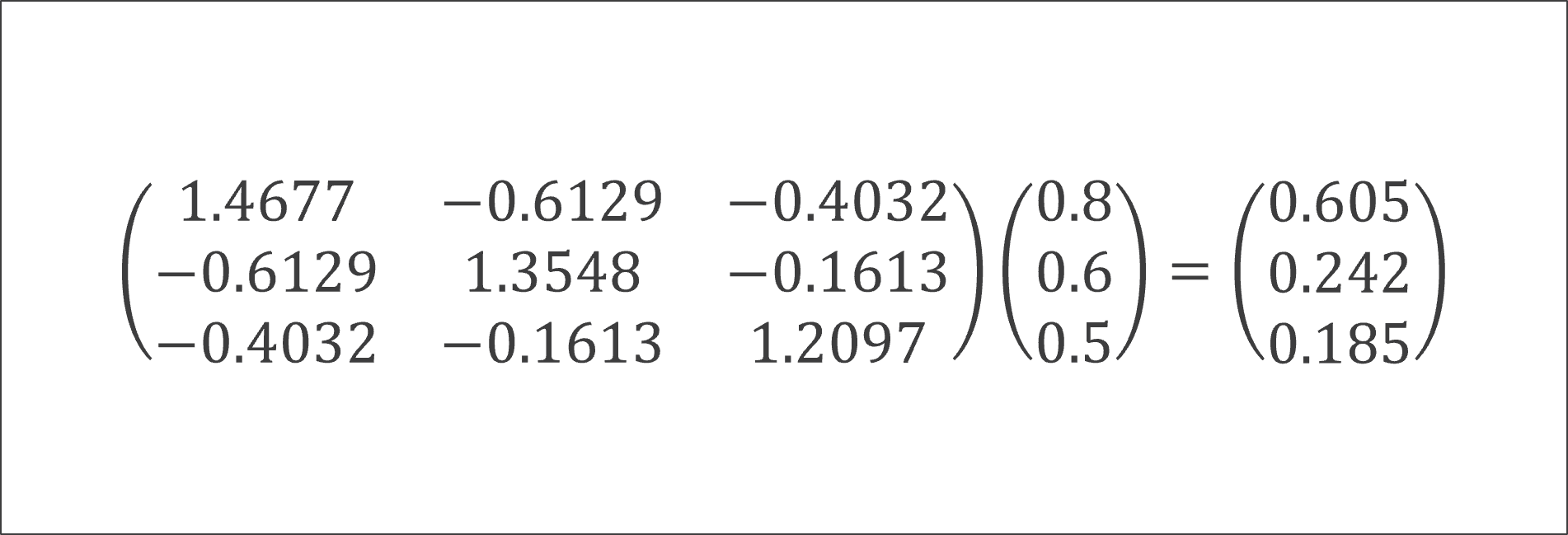この組織サーベイの結果から、一体何が言えるのだろう。人事部門でデータ分析に携わる人なら、こんな疑問を抱いたことがありませんか。50項目、100項目と多くの質問から成るアンケートの回答データを前に、どこから手をつければいいのか途方に暮れた経験はありませんか。

単純に平均値を出しても、大切な情報を見逃してしまうかもしれません。かといって、すべての項目を個別に分析するのは、あまりに時間がかかり、解釈も複雑になりすぎます。そして、「リーダーシップ」や「チームワーク」といった抽象的な概念を、どうやって数値化すればいいのでしょうか。

本コラムで紹介する「因子得点」は、こうした悩みを解決するための一つの手段になります。因子得点を使えば、膨大なデータの中に潜む情報を抽出し、解釈しやすい形に変換することができます。複雑に絡み合った質問項目の関係性を紐解き、重要度を考慮しながら、抽象的な概念を数値化することが可能です。

因子分析の基本

因子得点を理解する前に、まず因子分析について簡単に説明しましょう。因子分析とは、多数の観測変数（質問項目）の背後にある潜在的な要因（因子）を見つけ出す手法です[1]。

例えば、エンゲージメントサーベイで次の15個の質問があったとします[2]。

1. 同僚は必要な時に仕事上の助言をする
2. 上司は業務上の問題解決をサポートする
3. 必要な情報を得るためのネットワークがある
4. 業務に必要な道具が適切に提供されている
5. 困ったときに頼れる同僚がいる
6. 同僚は私の気持ちを理解している
7. 上司は私の個人的な悩みも聞く
8. 職場には信頼できる人間関係がある
9. 同僚との交流を通じてストレス解消ができる
10. 職場の雰囲気は温かく、受容的である
11. 同僚は私の仕事ぶりを正当に評価する
12. 上司は私の努力を認める
13. 私の貢献は組織内で適切に認識されている
14. 同僚からのフィードバックは建設的である
15. 私の能力が正当に評価されている

これらの質問項目に対する回答を分析すると、いくつかの共通する潜在的な要因（因子）が浮かび上がってきます。

• 因子1「道具的支援：具体的な支援を受けられること」（質問1-5に強く関連）
• 因子2「情緒的支援：心理面の支援を受けられること」（質問6-10に強く関連）
• 因子3「評価的支援：気後れせず適切な評価を受けられること」（質問11-15に強く関連）

因子分析は、潜在的な因子を導き出し、各質問項目がどの因子にどの程度関連しているかを「因子負荷量」として数値化します。因子負荷量とは、各質問項目が各因子にどの程度関連しているかを示します。例えば、質問1「同僚は必要な時に仕事上の助言をする」という項目の「道具的支援」因子に対する因子負荷量が0.6だった場合、この質問項目は「道具的支援」因子と比較的強く関連していると解釈できます。

因子得点とは

因子得点は、個々の回答者が各因子についてどのような特性を持っているかを数値化したものです。各回答者が因子分析によって抽出された潜在的な因子（今回の例では「道具的支援」「情緒的支援」「評価的支援」）にどの程度合致しているか、あるいはその特性をどの程度強く持っているかを表します。

例えば、ある従業員の「道具的支援」の因子得点が高ければ、その従業員は仕事上の具体的な支援を十分に受けていると感じています。逆に、「情緒的支援」の因子得点が低ければ、その従業員は職場における心理的なサポートが不足していると感じています。

因子得点を計算することで、直接観測することが難しい抽象的な概念を、個人レベルで数値化し、比較可能な形で表現することができます。具体的には、「道具的支援」「情緒的支援」「評価的支援」といった、直接目に見えない概念を、各個人がどの程度感じているかを数値として表現します。例えば、「Aさんは道具的支援をBさんよりも強く感じている」といった比較が可能になります。

因子得点の計算方法

因子得点の計算方法にはいくつかありますが、ここでは「回帰法」について説明します。回帰法は、各因子を成果指標、観測変数（質問項目）を影響指標とする重回帰式を作成することで因子得点を推定する方法です。ただし、実際の計算プロセスでは直接的に重回帰分析を行うわけではなく、因子負荷量と相関行列の逆行列を用いて因子得点係数を算出します。

回帰法による因子得点の計算手順を、具体例を交えながら説明していきます。

観測変数の標準化

すべての観測変数（質問項目の回答）を標準化します。標準化とは、平均を0、標準偏差を1に変換することです。例えば、ある回答者の「同僚は必要な時に仕事上の助言をする」という質問への回答が4（5段階評価の4）で、この質問項目の平均が3.5、標準偏差が1.2だったとします。すると、標準化された値は(4-3.5)/1.2=0.42となります。

もし標準化をしないと、異なるスケールの質問項目が因子得点に不均等な影響を与えてしまう可能性があります。例えば、1-5のスケールで測定された項目と1-7のスケールで測定された項目があった場合、後者の項目が不当に大きな影響を与えてしまうかもしれません。

1-7のスケールの項目は、その数値の範囲が広いため、因子得点の計算において、1-5のスケールの項目よりも大きな変動を生み出す可能性があります。これは、項目の重要性ではなく、測定スケールの違いによって生じる影響であり、望ましくありません。標準化することで、このような測定スケールの違いによる影響を排除し、各項目の重要性に基づいて因子得点を計算することができます[3]。

相関行列の計算と逆行列の算出

因子分析に用いる観測変数間の相関行列を計算し、その逆行列を求めます[4]。相関行列は、各質問項目間の相関係数を表す行列です。相関係数は、2つの変数間の線形関係の強さと方向を-1から+1の間の値で表します[5]。

逆行列とは、ある行列に掛けると単位行列（対角線上が1で他が0の行列）になる行列のことです。数学的には、行列Aに対してA^(-1)がAの逆行列であるとき、A*A^(-1)=A^(-1)*A=I（単位行列）となります。これは、逆行列が元の行列の「逆」の操作を行うものであることを意味しています。

相関行列をそのまま用いるのではなく、その逆行列を用いるのはなぜでしょうか。相関行列をそのまま用いる場合、変数間の相関関係が強いほど、それらの変数は因子得点の計算において過大に評価されます。これは、相関の強い変数が本質的に同じ情報を繰り返し提供しているにもかかわらず、それぞれが独立した情報源として扱われてしまうためです。

例えば、コラムで紹介した質問項目の中で、「同僚は必要な時に仕事上の助言をする」と「困ったときに頼れる同僚がいる」という2つの項目があります。これらは強く相関している可能性が高く、似た情報（同僚からの支援）を測定していると考えられます。相関行列をそのまま用いると、これら2つの項目は独立した2つの情報源として扱われ、「同僚からの支援」という要素が因子得点に二重にカウントされてしまいます。

一方、相関行列の逆行列を用いることで、この問題を解決できます。逆行列は、ある意味で相関関係の「逆」の操作を行います。具体的には、ある変数の影響を他の変数から「差し引く」働きをします。これによって、各変数の独自の貢献度、つまり他の変数では説明できない固有の情報を抽出することができます。

上記の例で言えば、逆行列を用いることで、「同僚は必要な時に仕事上の助言をする」という項目から、「困ったときに頼れる同僚がいる」という項目と重複する情報を差し引いた、「仕事上の助言」に関する情報を抽出できます。同様に、「困ったときに頼れる同僚がいる」という項目からも、「仕事上の助言」と重複する部分を差し引いた、「困ったときの支援」に関する情報を抽出できます。

このプロセスは、統計学的には「偏相関」の考え方に近いものです。他のすべての変数の影響を制御した上で、各変数が因子にどれだけ独自に寄与しているかを評価しているのです。

結果として、相関行列の逆行列を用いることで、各変数（質問項目）の独自の貢献度を評価し、より精密に因子得点を算出することができます。

なお、相関行列はシンプルである一方、逆行列の計算は複雑で、多くの計算ステップを必要とします。そのため、通常は統計ソフトを用いて算出します。

因子負荷行列の計算

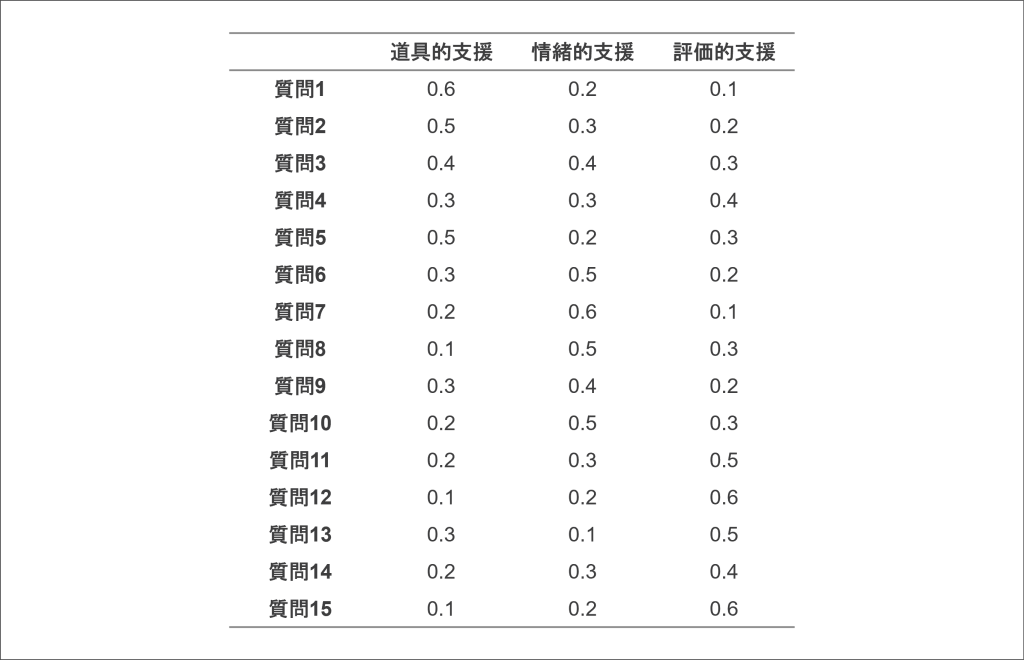
次に因子分析を行い、因子負荷行列を得ます。因子負荷行列は、各質問項目（行）が各因子（列）にどの程度関連しているかを示しています。例えば、次の因子負荷行列が得られたとします。

因子負荷行列は、各質問項目が各因子にどの程度関連しているかを意味しています。例えば、質問1は道具的支援との関連が比較的強く（0.6）、情緒的支援や評価的支援との関連は弱いことがわかります。因子負荷行列によって、どの質問項目がどの因子をよく表現しているかを把握することができます。

因子得点係数行列の計算

相関行列の逆行列と因子負荷行列の行列積（行列同士のかけ算）を取る形で掛け合わせて、因子得点係数行列を得ます。この操作によって、各観測変数（質問項目）が各因子の得点にどの程度寄与するかを示す係数（因子得点係数）を得ることができます。

このステップをイメージしやすくするために、簡単な例を考えてみましょう[6]。例えば、3つの質問項目と1つの因子がある場合を考えます。

相関行列の逆行列：

これは、3つの質問項目間の相関関係を調整するための行列です。対角要素が1より大きいことは、各変数の独自性を強調していることを示し、非対角要素が負であることは、変数間の相関を調整していることを示しています。

因子負荷行列：[0.8, 0.6, 0.5]

これは、3つの質問項目のそれぞれの因子負荷量を示しています。質問1の因子負荷量が0.8、質問2の因子負荷量が0.6、質問3の因子負荷量が0.5であることを意味します。

これらの行列を掛け合わせると、因子得点係数が得られます[7]。

相関行列の逆行列と因子負荷行列を掛け合わせるのは、因子負荷量（各質問項目と因子の関連の強さ）と相関行列の逆行列（質問項目間の相互関係の調整）の両方の情報を組み合わせて、各質問項目の純粋な寄与度を算出するためです。因子負荷量だけを見ると、質問項目間の重複を考慮できません。一方、相関行列の逆行列だけを見ると、因子との関連の強さを考慮できません。これらを掛け合わせることで、両方の情報を組み合わせることができるのです[8]。

その意味で、因子得点係数は、各質問項目の回答がそれぞれの因子得点にどれだけ影響を与えるかを数値化したものと言えます。例えば、ある質問項目の「道具的支援」因子に対する因子得点係数が0.5だった場合、その質問項目の標準化された回答値が1単位増加すると、「道具的支援」の因子得点が0.5単位増加することを意味します。これは、重回帰分析における偏回帰係数と同様の解釈ができます。他の質問項目の影響を制御した上で、その質問項目が因子得点にどれだけ寄与するかを表しているということです。

因子得点の計算

最後に、得られた因子得点係数と標準化された観測変数（質問項目の回答）の値を掛け合わせます。各回答者の標準化された回答値に対応する因子得点係数を掛け、それらを合計することで因子得点を算出します。

因子得点=Σ(因子得点係数×標準化された回答値)

この式は、各質問項目の標準化された回答値に、その質問項目の因子得点係数を掛け、それらをすべて足し合わせることを意味します。具体例を考えてみましょう。ある回答者の「道具的支援」因子の得点を計算する場合を考えます。

この場合、「道具的支援」の因子得点は次のように計算することができます。

(0.5*0.4)+(-0.2*0.3)+(1.0*0.2)+(0.3*0.1)+(-0.5*0.3)+(0.7*0.1)+(-0.1*0.05)+(0.2*0.02)+(0.4*0.1)+(-0.3*0.05)+(0.6*0.05)+(0.1*0.02)+(-0.4*0.1)+(0.3*0.05)+(-0.2*0.02)

=0.2+(-0.06)+0.2+0.03+(-0.15)+0.07+(-0.005)+0.004+0.04+(-0.015)+0.03+0.002+(-0.04)+0.015+(-0.004)

=0.321

この計算を各因子について行うことで、個々の回答者の因子得点が得られます。すなわち、各回答者について、「道具的支援」「情緒的支援」「評価的支援」それぞれの因子得点が計算されることになります。これによって、各回答者が各因子についてどの程度の特性を持っているかを数値化して表現することができます。

因子得点の解釈

因子得点は通常、平均0、標準偏差1の標準正規分布に従うように計算されます。各回答者の因子得点を、全回答者の因子得点の平均が0、標準偏差が1になるように調整しています。

標準正規分布は、データの分布を一定の形に標準化したもので、統計的分析の基礎となる重要な分布です。この分布は、平均を中心に左右対称の釣鐘型の形状を持ち、全体の約68%のデータが平均から±1の範囲内に、約95%のデータが±2の範囲内に収まるという特徴があります。

この標準正規分布の特性を利用して、因子得点が0の場合、その因子について平均的であり、正の値は平均より高く、負の値は平均より低いと捉えることができます。

さらに詳しく見ていくと、因子得点が±1の場合、平均から1標準偏差離れています（全体の約68%が±1の範囲内です）。これは、因子得点が-1から+1の間にある回答者が、全体の約68%を占めるということです。例えば、ある従業員の「道具的支援」の因子得点が0.5だった場合、その従業員は平均よりやや高い道具的支援を認識していますが、それほど極端ではないと解釈できます。

因子得点が±2の場合、平均から2標準偏差離れています（全体の約95%が±2の範囲内です）。因子得点が-2から+2の間にある回答者は、全体の約95%を占めます。この範囲を超える得点は「かなり高い」あるいは「かなり低い」と解釈できます。例えば、ある従業員の「情緒的支援」の因子得点が2.1だった場合、その従業員は非常に高いレベルの情緒的支援を認識していると捉えられます。

因子得点の特徴

因子得点の特徴を理解するために、「尺度得点」と比較してみましょう。

尺度得点は、同じ概念を測定していると考えられる質問項目の得点を合計または平均したものです。例えば、「道具的支援」に関する5つの質問の回答（1-5の5段階評価）を単純に平均して、その人の「道具的支援」尺度得点とするような方法です。

一方、因子得点は、ここまで説明した通り、複雑な統計的手法を用いて算出されます。因子得点の計算では、各質問項目の重要度（因子負荷量）を考慮します。具体的には、因子負荷行列を用いることで、各質問項目の重要度を反映させています。因子負荷量が高い項目ほど、最終的な因子得点に影響を与えるのです。

因子得点の計算では他の因子との関連性も考慮されます。これは、ある質問項目が複数の因子に関連している可能性を考慮に入れるためです。例えば、「上司は業務上の問題解決をサポートする」という質問は、「道具的支援」だけでなく「情緒的支援」にも関連している可能性があります。因子得点の計算では、このような複雑な関係性を統計的に処理し、各因子の影響を抽出します。

しかし、解釈の面では、尺度得点は元の回答スケールに基づいているため、直感的に理解しやすいという利点があります。例えば、5段階評価で平均が4.2という尺度得点は、回答選択肢の意味（例：5が「非常にそう思う」、1が「全くそう思わない」）を参照することで、「かなり肯定的な評価」と解釈できます。

他方で、因子得点は計算プロセスにおいて標準化を経ているため、相対的な位置づけは分かりやすいのですが、絶対的な意味の解釈は難しくなります。例えば、因子得点が1.5という値は、平均よりも1.5標準偏差高いことを示しますが、これが具体的にどの程度「高い」のかを直感的に理解するのは難しいかもしれません。

さらに、尺度得点と因子得点では、その後の分析を進める際に違いが出てくる場合があります。特に、質問項目間のα係数（内的整合性）が低い場合、尺度得点を用いると相関の希薄化が生じる可能性があります[9]。内的整合性が低い場合、尺度得点を用いると、各質問項目に含まれる測定誤差の影響が大きくなり、結果として他の変数との相関が実際よりも弱く観測されてしまいます。

対して、因子得点は測定誤差の影響を軽減する方法で計算されるため、この問題をいくらか軽減することができます。因子分析では、各質問項目に共通する分散（共通性）と、各質問項目に固有の分散（固有性）を分離します。因子得点の計算では、主に共通性の部分を利用するため、個々の質問項目の測定誤差の影響を軽減することができます。

具体的には、因子分析では各質問項目の因子負荷量を計算する際に、その項目がどの程度因子によって説明されるかを考慮します。測定誤差が大きい（つまり、因子との関連が弱い）項目は、自動的に因子得点の計算において重みが小さくなります。

脚注

[1] 因子分析に関する詳細は当社コラムをご覧ください。

[2] 本コラムで示す例はすべて架空のものです。その点、ご注意ください。

[3] なお、同じ1-5のスケールで測定された項目であっても、それぞれが測定している内容が異なることからスケールは本質的に違っていると見なされます。そのため、因子得点の計算においては、同じスケールで測定した項目や指標でも標準化をする必要があります。

[4] 相関行列の逆行列を用いる際、多重共線性の問題が生じ得ます。多重共線性とは、項目間に非常に強い相関関係がある際に生じる問題を指し、これが存在すると相関行列の逆行列の計算が不安定になることがあります。これによって、因子得点の推定が不安定になったり、誤差が大きくなったりする可能性があります。多重共線性への対処としては、強い相関を持つ項目や指標の一方を分析から除外する方法があります。

[5] 相関係数についての詳細は当社コラムが参考になります。

[6] 本コラムでは簡略化のためシンプルな行列例を取り上げますが、実際の因子分析では多くの場合、より大きな行列を扱います。この場合、計算過程は複雑になり、手計算は現実的ではありません。そのため、通常は統計ソフトを利用して計算を行います。

[7] 計算プロセスを紹介しましょう。ここには、2つの行列があります。1つは相関行列の逆行列で、注釈7上部にある3行3列の逆行列です。もう1つは因子負荷行列で、[0.8,0.6,0.5]という3行1列の行列です。

これらを掛け合わせる際、3行3列の行列と3行1列の行列の乗算を行います。行列の乗算の基本的な性質により、結果は3行1列の行列となります。

具体的には、m×n行列とn×p行列を掛け合わせると、結果はm×p行列になるという原則に従っています。この場合、3×3行列（相関行列の逆行列）と3×1行列（因子負荷行列）を掛け合わせるので、結果は3×1行列、つまり3行1列となるわけです。

計算の第一ステップでは、相関行列の逆行列の最初の行[1.4677,-0.6129, -0.4032]と因子負荷行列の列[0.8, 0.6, 0.5]を使います。この計算方法は行列の乗算の定義に基づいています。行列の乗算では、左側の行列の行と右側の行列の列の対応する要素を掛け、それらを合計します。

したがって、1.4677に0.8を掛け、-0.6129に0.6を掛け、-0.4032に0.5を掛け、これらを足し合わせます。つまり、(1.4677×0.8)+(-0.6129×0.6)+(-0.4032×0.5)=1.174194-0.36774-0.20161≒0.605となります。これが結果の最初の要素です。

第二ステップでも、同様に行列の乗算の定義に従って計算を行います。相関行列の逆行列の2行目[-0.6129,1.3548,-0.1613]と因子負荷行列の列[0.8, 0.6, 0.5]を使って、同様の計算を行います。

したがって、-0.6129に0.8を掛け、1.3548に0.6を掛け、-0.1613に0.5を掛け、これらを足し合わせます。つまり、(-0.6129×0.8)+( 1.3548×0.6)+( -0.1613×0.5)=-0.49032+0.812903-0.08065≒0.242となります。これが結果の2つ目の要素です。

第三ステップも同様に計算を行うと、そのプロセスは割愛して、値はおよそ0.185となります。これが結果の3つ目の要素です。

これらの計算ステップは、行列の乗算を要素ごとに分解して行っています。全体として、この過程は(3×3)行列と(3×1)行列の乗算を表しており、その結果として(3×1)行列が得られます。そして、最終的な結果は[0.605, 0.242, 0.185]となります。

[8] ２因子以上の因子解を持つ因子分析では、ここまでの計算で得られた因子得点係数行列にさらに因子間相関行列もかけ算し、最終的な因子得点行列係数を算出します。因子得点の算出において、複数の因子間でどの程度関連性があるかも加味するため、因子間相関行列も因子得点係数の計算に含めるよう構成されています。

[9] 相関の希薄化に関する詳細は当社のα係数に関するコラムをご確認ください。

---

執筆者

伊達 洋駆　株式会社ビジネスリサーチラボ 代表取締役
神戸大学大学院経営学研究科 博士前期課程修了。修士（経営学）。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、組織サーベイや人事データ分析のサービスを提供している。著書に『60分でわかる！心理的安全性 超入門』（技術評論社）や『現場でよくある課題への処方箋 人と組織の行動科学』（すばる舎）、『越境学習入門 組織を強くする「冒険人材」の育て方』（共著；日本能率協会マネジメントセンター）などがある。2022年に「日本の人事部 HRアワード2022」書籍部門 最優秀賞を受賞。東京大学大学院情報学環 特任研究員を兼務。