2024年12月10日
決定係数:「説明」とは何か
回帰分析[1]を行った際に「決定係数(R2)」というものが算出されます。この決定係数は、分析結果の意味を読み解く上で大事な指標なのですが、理解が難しいという声もよく聞きます。
決定係数は、いわゆる「説明力[2]」を数値化したものであり、「成果指標の分散を説明している」などと述べるのですが、そもそも「説明(力)」という言葉自体が抽象的で、何を意味するのかつかみにくいものです。
そこで本コラムでは、決定係数の考え方を解説します。できる限り理解しやすいよう、具体例も交えながら説明していきます。本コラムを通じて、決定係数が何を指すものかを理解していただけると幸いです。
ばらつきを説明するということ
「ばらつき」という言葉を聞いて、皆さんは何を想像しますか。組織サーベイの文脈で考えてみましょう。
例えば、1000人の従業員に対してエンゲージメント(成果指標)を1-10の尺度で聞いたとします。結果を見ると、ある人は10、ある人は1、多くの人は中間的な値をつけていることでしょう。このエンゲージメントの違い、つまり「ばらつき」はなぜ生じるのでしょうか。
ばらつきを「説明する」とは、そのばらつきの要因を特定し、その要因がどの程度ばらつきに寄与しているかを明らかにすることです。例えば、「仕事の自律性」という影響指標を考えてみましょう。
仕事の自律性が高い従業員ほどエンゲージメントが高く、自律性が低い従業員ほどエンゲージメントが低いという傾向があれば、「仕事の自律性」はこのばらつきを「説明している」と言えます。エンゲージメントのばらつきの一部は、仕事の自律性の違いによって生じていると考えられるのです。
しかし当然ながら、仕事の自律性だけでは説明できない部分もあります。ある従業員は仕事の自律性は高くても、別の理由でエンゲージメントが低いかもしれません。または、自律性は低くても、上司との良好な関係性でエンゲージメントが高いかもしれません。
決定係数(R2)は、こうした「説明できる部分」と「説明できない部分」の割合を数値化したものです。例えば、決定係数が0.35であれば、エンゲージメントのばらつきの35%は仕事の自律性で説明でき、残りの65%は他の要因や偶然などによるものだと解釈できます。
この「説明力」を理解することは、組織の改善に直結します。例えば、仕事の自律性がエンゲージメントのばらつきの35%を説明しているのであれば、従業員の自律性を高める施策を講じることで、組織全体のエンゲージメントを向上させられる可能性があると言えるでしょう[3]。
一方で、決定係数が低い場合(例えば0.05)、仕事の自律性以外の要因(上司との関係性、職場の助け合いなど)が大きな影響を与えている可能性があります。この場合、自律性の向上だけでなく、他の要因も同時に検討する必要があるでしょう。
決定係数の導き出し方
決定係数(R2)は次のような式で導き出すことができます。
R2=SSR/SST=1-(SSE/SST)
ここで、いくつかの略語が出てきて面食らったかもしれません。
- SST(Total Sum of Squares):全変動の平方和
- SSR(Regression Sum of Squares):回帰変動の平方和
- SSE(Error Sum of Squares):残差変動の平方和
これらの要素を詳しく見ていきましょう。そうすれば、決定係数の意味するところがわかってきます。
SST:データの全体的なばらつき
SST(全変動の平方和)は、成果指標のデータ全体のばらつきを表します。これは、各回答者で成果指標のデータと全体の平均との差を二乗し、合計したものです。次の手順で計算することができます。
- データの平均値を計算する
- 各データから平均値を引き、その差を求める
- その差を二乗する
- 全てのデータについて、2と3の操作を行い、その結果を合計する
例を挙げましょう。成果指標として、5人の従業員のエンゲージメントスコアが7, 8, 6, 9, 5だったとします[4]。この平均値は7です。各スコアと平均値の差の二乗は次のように求められます。
(7-7)2+(8-7)2+(6-7)2+(9-7)2+(5-7)2=0+1+1+4+4=10
この10がSSTとなります。SSTが大きいほど、データのばらつきが大きいことを意味します。例の場合は、SSTが大きいと、従業員間でエンゲージメントのレベルに大きな差があることを示しています。ある従業員は非常に高いエンゲージメントであるのに対して、別の従業員は非常に低いエンゲージメントであるような状況です。一方、SSTが小さい場合、多くの従業員が似たようなレベルのエンゲージメントであることを意味します。
SSR:モデルで説明できるばらつき
SSR(回帰変動の平方和)は、回帰式[5]によって説明できるばらつきを表します。これは、回帰式による予測値と全体の平均との差を二乗し、合計したものです。計算手順は次の通りです。
- 回帰式を使って、各データの予測値を計算する
- データ全体の平均値を計算する
- 各予測値から平均値を引き、その差を求める
- その差を二乗する
- 全てのデータについて、3と4の操作を行い、その結果を合計する
例えば、エンゲージメント(成果指標)と仕事の自律性(影響指標)の関係を分析し、次の回帰式が得られたとします。
エンゲージメント=2+0.7×(仕事の自律性)
仕事の自律性スコアが6, 8, 5, 9, 4だった場合、回帰式から予測されるエンゲージメントのスコアはそれぞれ6.2, 7.6, 5.5, 8.3, 4.8となります。
エンゲージメントの平均が7だとすると、SSRは次のように求められます。
(6.2-7)2+(7.6-7)2+(5.5-7)2+(8.3-7)2+(4.8-7)2=0.64+0.36+2.25+1.69+4.84=9.78
この9.78がSSRとなります。SSRが大きいほど、モデルの説明力が高いことを意味します。SSRが大きい場合、仕事の自律性がエンゲージメントのばらつきをよく説明できていることを示しています。仕事の自律性の違いが、エンゲージメントの違いをよく反映していると解釈できます。一方、SSRが小さい場合、仕事の自律性はエンゲージメントのばらつきをあまり説明できていないことを指します。
SSE:説明しきれなかったばらつき
SSE(残差変動の平方和)は、回帰式で説明できなかったばらつきのことです。実際の観測値と回帰式による予測値との差(残差)を二乗し、合計したものです。次の手順で計算します。
- 回帰式を使って、各データの予測値を計算する
- 各データの実際の観測値から予測値を引き、残差を求める
- その残差を二乗する
- 全てのデータについて、2と3の操作を行い、その結果を合計する
先ほどの例を続けましょう。実際のエンゲージメントスコアが7, 8, 6, 9, 5だった場合、SSEは次のように求められます。
(7-6.2)2+(8-7.6)2+(6-5.5)2+(9-8.3)2+(5-4.8)2=0.64+0.16+0.25+0.49+0.04=1.58
この1.58がSSEとなります。SSEが小さいほど、回帰式の当てはまりが良いことを意味します。例で言えば、SSEが小さい場合、実際のエンゲージメントスコアと、仕事の自律性から予測されるエンゲージメントスコアの差が小さいことを表しています。仕事の自律性がエンゲージメントをよく説明できているということです。逆に、SSEが大きい場合、仕事の自律性以外の要因がエンゲージメントに大きく影響している可能性があります。
決定係数の解釈
決定係数の式に戻りましょう。
R2=SSR/SST=1-(SSE/SST)
SSTは元々のデータのばらつき全体、SSRは回帰式で説明できたばらつき、SSEは説明できなかったばらつきを表しています。
SSR/SSTは「説明できたばらつきの割合」を意味し、これが決定係数です。全体のばらつき(SST)のうち、モデルで説明できたばらつき(SSR)の割合を表しています。例えば、SSR/SST=0.40であれば、エンゲージメントのばらつきの40%を仕事の自律性で説明できていることになります。
そして、SSE/SSTは「説明できなかったばらつきの割合」を表します。これは、回帰式では説明できなかった部分、つまり他の要因や偶然などによる変動の割合を示しています。
したがって、1-(SSE/SST)も「説明できたばらつきの割合」、すなわち決定係数を意味します。この式は、全体のばらつきから説明できなかった部分を引くことで、説明できた部分を求めているのです。
先の例をいったん振り返り、例えばSSR=40、SST=100だったとすると、R2=40/100=0.40となります。この場合、決定係数は0.40となり、仕事の自律性がエンゲージメントのばらつきの40%を説明しているということでした。
この残りの60%(SSE/SST=60/100=0.60)は、回帰式で説明できなかった部分、つまり他の要因や偶然などによる変動と解釈できます。この部分は、例えば上司との関係性や職場の助け合いなど、回帰式に含まれていない他の要因の影響や、測定誤差などによるものと考えられます。
決定係数を理解することで、どの程度、回帰式がデータを説明できているか、そして何か重要な要因を見逃していないかを検討することができます。例えば、決定係数が0.40のモデルは、十分な説明力を持っていると言えます。一方、決定係数が0.05のモデルは説明力が低く、他の重要な要因を考慮する必要があるかもしれません。
決定係数の視覚的理解
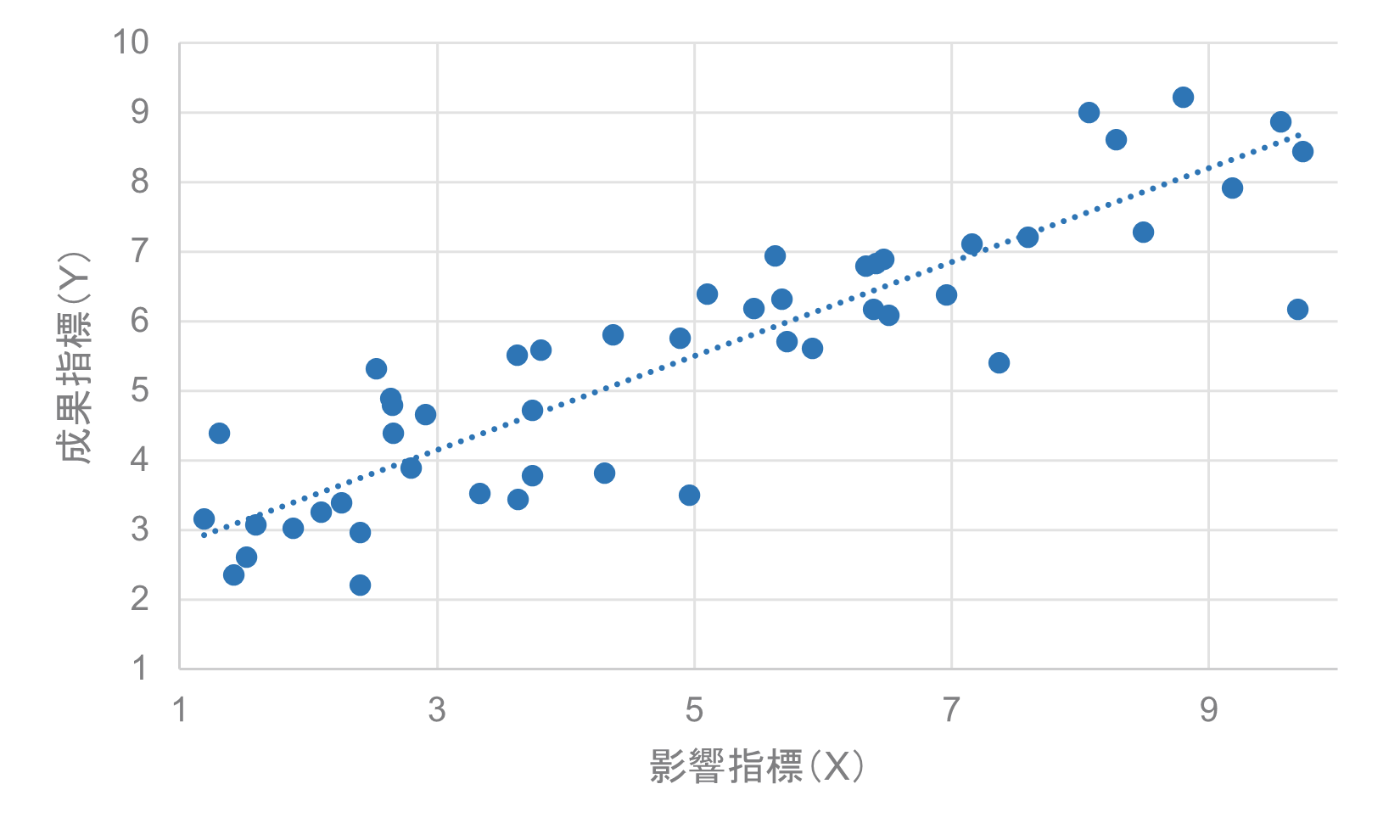
決定係数の考え方を直感的に理解するために、散布図を用いると良いでしょう。次の図は、ある影響指標(X軸)と成果指標(Y軸)の関係を示す散布図です。
この図では、複数の点がデータを表しています。これらの点は、各従業員の影響指標の値(X軸の値)と対応する成果指標の値(Y軸の値)を示しています。例えば、組織サーベイでは、各点が一人の従業員を表し、その従業員の「仕事の自律性」(影響指標)とそれに対応する「エンゲージメントスコア」(成果指標)を指していると考えられます。
図中の直線は回帰直線と呼ばれ、データの全体的な傾向をよく表す直線です。この直線は、データ全体の傾向をよく表現するように引かれています。
また、各データから回帰直線までの間の距離は残差と呼ばれます。残差は、実際の成果指標の値(データのY座標)と回帰直線から予測される値(回帰直線上のY座標)との差を表しています。回帰式では説明できない部分、予測値からのずれを意味しています。
言ってみれば、決定係数(R2)は、これらのデータが回帰直線にどれだけ近いかを数値化したものです。データの全体的なばらつき(総変動)のうち、回帰直線によって説明できる部分(回帰変動)の割合を示しています。影響指標(X)によって成果指標(Y)のばらつきがどの程度説明できるかを表す指標です。
決定係数が1に近いほど、各データを表す個々の点は回帰直線に近い位置にあり、モデルの当てはまりが良いことを表します。影響指標が成果指標のばらつきをよく説明できているということです。視覚的には、ほとんどすべてのデータが回帰直線上かそのごく近くに位置し、残差が非常に小さい状態です。これは、影響指標の値から成果指標の値をかなり正確に予測できることを示唆しています。
一方、決定係数が0に近いほど、データは回帰直線から離れており、モデルの当てはまりが悪いことを表します。この場合、影響指標は成果指標のばらつきをあまり説明できていないと解釈できます。散布図上では、データが回帰直線の周りに広く散らばっており、大きな残差が多く見られる状態です。これは、影響指標の値から成果指標の値を予測することが困難であることを意味します。
ここで、散布図をよく観察すると、決定係数の説明が相関係数と似ているように感じられないでしょうか。実際、単回帰分析(影響指標が1つの回帰分析)の場合、決定係数は相関係数と密接な関係があります。
単回帰分析の場合、決定係数(R2)は相関係数(r)の2乗になります[6]。これは次のように説明できます。
- 相関係数(r)は、2つの変数間の線形関係の強さと方向を-1から+1の間で表す
- 決定係数(R2)は、成果指標(Y)の変動のうち、影響指標(X)によって説明される割合を0から1の間で表す
- 単回帰分析では、XとYの関係を最もよく表す直線(回帰直線)を求める
- この直線によって説明される変動の割合が決定係数となる
- 数学的に、この「説明される変動の割合」は、相関係数を2乗したものに等しくなる
これは、相関係数が正負の方向を持つのに対し、決定係数は常に正の値(割合)を示すことにも対応します。例えば、相関係数が0.6でも-0.6でも、決定係数は0.36になります。
この関係により、散布図上で点がより直線的に並んでいるほど(つまり、相関が強いほど)、決定係数は1に近づきます。逆に、点が無秩序に散らばっているほど(相関が弱いほど)、決定係数は0に近づきます。
F検定:回帰式の有意性を確認する
F検定は、回帰式全体の有意性を検証するための手法です。決定係数の解釈において、F検定は重要な役割を果たします。なぜなら、決定係数が統計的に意味のある値なのかを判断するためにF検定を用いることができるからです[7]。
例えば、サンプルサイズが小さい場合や、多くの影響指標を使用している場合、決定係数が高くなることがあります。しかし、そのような場合も、F検定を行うことで統計的に有意であるかどうかを確認でき、結果をより適切に解釈することができます。
F検定では、F値(またはF比)という指標を用います。F値は次のように計算します。
F=(SSR/df_regression)/(SSE/df_error)
SSR(回帰変動の平方和)とSSE(残差変動の平方和)については既に詳細に説明しているので大丈夫でしょう。残る2つの指標はそれぞれ次のことを意味します。
- df_regression:回帰の自由度(通常、影響指標の数)
- df_error:誤差の自由度(サンプル数–影響指標の数-1)
F値の式は、回帰式で説明できる分散(SSR/df_regression)と、説明できない分散(SSE/df_error)の比を表しています。簡単に言えば、F値は「説明できる分散」が「説明できない分散」の何倍あるかを示しているということです。
具体的に考えてみましょう。例えば、1000人の従業員を対象に、3つの影響指標(仕事の自律性、上司との関係性、職場の助け合い)を用いてエンゲージメントを予測する重回帰式を構築したとします。
SSR(説明できる変動)が400、SSE(説明できない変動)が600だった場合、次の通り、F値を算出できます。
F=(400/3)/(600/996)≒221.33
このF値は、重回帰式が説明できる分散が、説明できない分散の約221.33倍であることを示しています。
F値が大きいほど、回帰式が統計的に有意である可能性が高くなります。具体的には、計算されたF値を、指定された有意水準(0.05であることが多い)とdf_regressionおよびdf_errorに基づいて決定される臨界値と比較します。ここにおける臨界値とは、「F値がこれより大きければ統計的に意味がある」という境界線となる値です。
例えば、有意水準0.05、df_regression=3、df_error=996の場合、F分布表から臨界値を求めると約2.61となります。先ほどの例でF値が221.33だったことを考えると、このF値は臨界値をはるかに上回っています。
F値が臨界値よりも大きい場合、回帰式は統計的に有意であると判断することができます。少なくとも「回帰式全体で、成果指標の変動がいくらか説明されている」と考えられます。この例の場合、回帰式は有意であり、選択した影響指標(仕事の自律性、上司との関係性、職場の助け合い)でエンゲージメントの変動が説明されていることが示されています。
一方、F値が臨界値よりも小さい場合、回帰式全体が統計的に有意ではないと判断することができます。これは、選択した影響指標ではエンゲージメントの変動を説明できないことを示唆しています。
F検定は、決定係数と組み合わせて解釈することが効果的です。例えば、決定係数が0.40で、F検定も有意であれば、決定係数の値からその回帰式は十分な説明力を持ち、それが統計的にも信頼できると有意な結果から判断できます。一方、決定係数が高くてもF検定が有意でない場合は、その結果を慎重に解釈する必要があります。
決定係数の限界と注意点
決定係数は有用な指標ですが、いくつかの限界や注意点があります。これらを理解することで、誤った結論を導き出すリスクを減らすことができます。
- 因果関係の証明ではない:決定係数が高く回帰モデルで成果指標を説明できそうだからといって、必ずしも因果関係があるとは限りません。決定係数の分析はデータの相関関係を表すものであり、相関関係と因果関係は異なるものです。相関関係は二つの変数間の関連性を示すものですが、因果関係はある変数が他の変数に直接的な影響を与えていることを意味します。
- 非線形関係の見落としに注意する:決定係数は線形関係を前提としていますが、実際の関係は非線形である可能性があります。線形関係とは、一方の変数が増加(または減少)すると、もう一方の変数も比例して増加(または減少)する関係を指します。しかし、現実の組織では、このような関係性だけでなく、より複雑な非線形の関係が存在することがあります。
- 外れ値の影響を受ける:決定係数は外れ値(極端な値)の影響を受けやすいという特徴があります。外れ値とは、他のデータから大きく離れた値のことを指します。少数の極端なデータポイントが、全体の結果を歪める可能性があります。
脚注
[1] 回帰分析そのものの詳細な解説は当社コラムを別途ご確認ください。
[2] 本文中で「説明する」という表現を使用していますが、これは統計的な関連性を表すものであり、因果関係を意味するものではありません。決定係数が高くても、それは変数間の強い相関関係を示すに過ぎず、直接的な因果関係の証明にはなりません。
[3] 決定係数の値の解釈には唯一の基準があるわけではありません。0.13以下は弱い説明力、0.13から0.26は中程度の説明力、0.26以上は強い説明力を示すという考え方もありますが、人や組織をめぐる現象では、0.13程度でも十分に意味のある結果とされることがあります。
[4] 本コラム内の計算例では、概念をわかりやすく説明するために、少数サンプルを用いています。少数サンプルを使用することで、決定係数やF値の計算過程を簡潔に示すことができますが、実際のデータ分析においてはサンプルサイズには注意が必要です。少数サンプルでは、結果が外れ値や特定のデータに強く影響されるため、分析結果の安定性が低下する可能性があります。また、統計的有意性を確認する際も、サンプルが少ないと信頼できる結論を得ることが難しくなります。
[5] 本コラムでは「回帰式」という用語を使用していますが、統計学では「回帰モデル」とも呼ばれます。両者は実質的に同じ事柄を指し、文脈に応じて使い分けられることがあります。
[6] 影響指標と成果指標の相関係数の2乗が決定係数になるのは単回帰分析の場合に限られます。重回帰分析(複数の影響指標を使用)では、回帰式を使って計算される各回答者の予測値のデータと実測値のデータの相関を二乗した値が決定係数と一致します。
[7] F検定は回帰式全体の有意性を検証します。これは、その回帰式によって成果指標の変動が説明できているかを検証しており、説明割合を表す決定係数がゼロであるという帰無仮説を検定します。一方、後に個々の回帰係数の有意性を検証する際にはt検定が用いられ、各回帰係数がゼロと有意に異なるかどうかを判断します。
F検定とt検定の結果は必ずしも一致しません。F検定が有意であっても、すべてのt検定が有意とは限りません。逆に、一部のt検定が有意でなくても、F検定は有意になる可能性があります。
執筆者
 伊達 洋駆 株式会社ビジネスリサーチラボ 代表取締役
伊達 洋駆 株式会社ビジネスリサーチラボ 代表取締役
神戸大学大学院経営学研究科 博士前期課程修了。修士(経営学)。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、組織サーベイや人事データ分析のサービスを提供している。著書に『60分でわかる!心理的安全性 超入門』(技術評論社)や『現場でよくある課題への処方箋 人と組織の行動科学』(すばる舎)、『越境学習入門 組織を強くする「冒険人材」の育て方』(共著;日本能率協会マネジメントセンター)などがある。2022年に「日本の人事部 HRアワード2022」書籍部門 最優秀賞を受賞。東京大学大学院情報学環 特任研究員を兼務。