人事領域のデータ分析において、相関分析と回帰分析はよく用いられる手法でしょう。両者は一見似ているため、混同されがちですが、実際にはそれぞれ異なる情報を提供してくれます。本コラムでは、人事担当者の皆さんに向けて、この二つの手法の違いを解説します。

相関分析と回帰分析は、どちらも変数間の関係性を調べるために使われます。例えば、従業員の満足度と生産性の関係を調べたい場合、これらの手法が役立ちます。しかし、それぞれが示す「関係性」の意味は異なります。その違いを理解することで、データをより深く解釈することができます。

本コラムでは、相関分析と回帰分析の基本的な考え方を説明し、続いて、それぞれの計算方法や解釈の仕方を見ていきます。そして、両者の違いを、具体例を交えながら説明します。これらの分析手法をどのように使い分け、どのように結果を解釈すべきかについても述べます。

データ分析は、組織の意思決定において重要な役割を果たします。相関分析と回帰分析の違いを理解することで、適切な施策の立案や、効果的な人材マネジメントにつながるでしょう。

相関分析の考え方

相関分析は、2つの変数間の関係の強さと方向性を検討する手法です[1]。人事領域では、例えば、従業員の勤続年数と給与の関係、トレーニング時間とパフォーマンスの関係など、様々な要素間の関連性を調べるのに用いることができます。

相関分析において重要な指標は、相関係数(r)です。相関係数は-1から+1の間の値をとり、次のように解釈することができます。

• r=1：完全な正の相関（一方が増加すると、他方も増加）
• r=0：相関なし（2つの変数間に線形の関係がない）
• r=-1：完全な負の相関（一方が増加すると、他方は減少）

例えば、勤続年数と給与の相関係数が.80だった場合、これは強い正の相関を表しています。勤続年数が長い従業員ほど、給与も高い傾向にあることを意味します[2]。

相関係数の計算式は次の通りです。

r=Σ((x-)(y-))/(n*)

この式が意味するところを簡単に解説しましょう。(x-)と(y-)は、それぞれの変数の「偏差」を表しています。各データが平均からどれほど離れているかを表しています。

これらの偏差を掛け合わせることで、共分散を計算しています。共分散は、二つの変数が同じ方向に変化するか、逆方向に変化するかを示す指標です。例えば、Xが平均より高いときにYも平均より高い傾向がある場合、共分散は正の値になります。逆に、Xが平均より高いときにYが平均より低い傾向がある場合、共分散は負の値になります。

Σ(x-)^2*Σ(y-)^2/n

Σ((x-)(y-))は、これらの偏差の積の総和を取っています。これによって、データ全体を通じて、二つの変数がどの程度一貫して同じ方向（または逆方向）に変化しているかを算出しています。

なお、この指標はデータの個数が多くなるほど値が大きくなる特徴があるため、nで割り算することでその影響を抑えています。

分母のはxとyそれぞれの標準偏差を表し、各変数のばらつきを考慮に入れるためのものです。

この操作により、変数の単位や尺度の違いによる影響を除去することができ、相関係数を-1から1の間に標準化しています。

相関係数の式は「二つの変数が同じ方向（または逆方向）に変化する傾向の強さ」を、-1から1の間の数値で表現しているということです。例えば、相関係数が.80の場合、二つの変数は強い正の関連性を持ち、一方が増加するとき、他方も増加する傾向が強いことを意味しています。逆に、-.80の場合は、一方が増加するとき、他方は減少する傾向が強いことを指します。

回帰分析の考え方

回帰分析は、影響指標が成果指標とどのような関連があるかを検討する手法です。成果指標とは、人や組織の目指すべき状態を表す指標を指します。一方、影響指標は、成果指標を促進または阻害する要因を表す指標です。

最も基礎的な回帰分析は単回帰分析であり、その式は次のように表現できます。

Y=a+bX+ε

Yは成果指標、Xは影響指標、aが切片（Xが0のときのYの値）、bは回帰係数、εが誤差項をそれぞれ意味します。

回帰分析で重要となる指標の一つは回帰係数（b）です。回帰係数は、影響指標が1単位変化したときに、成果指標がどれほど変化するかを表しています。例えば、満足度（1-5のスケール）と生産性（1日あたりの生産量）の関係を分析し、回帰係数が10だった場合、これは「満足度が1ポイント上がると、生産量が平均して10単位増加する」という関連があることを意味します。

回帰分析におけるもう一つの重要な指標は決定係数（R²）です。これは、回帰モデル（回帰式の右辺）が成果指標の変動をどの程度説明できるかを示す指標です。影響指標の変化によって説明される成果指標の変動の割合を表します。例えば、R²=.30の場合、影響指標の変化が成果指標の変動の30%を説明しているということです[3]。

R²は0から1の間の値をとり、1に近いほど回帰モデルの説明力が高いことを表します。例えば、R²=.70では、成果指標の変動の70%を説明していることになりますが、R²=.01では、成果指標の変動の1%しか説明できておらず、他の大事な要因が考慮されていない可能性があると考えられます。

相関分析と回帰分析の違い

相関分析と回帰分析は、どちらも変数間の関係を調べる手法です。しかし、いくつかの点で違いがあります。

目的の違い

• 相関分析：2つの変数がどの程度一緒に変動するかを検討する
• 回帰分析：影響指標が成果指標とどのような関連があるかを検討する

相関分析は、二つの変数の値が互いにどのように変化するかを見ています。例えば、従業員の満足度と生産性を考えると、「満足度が高い従業員は生産性も高い傾向にあるか」「満足度が低い従業員は生産性も低い傾向にあるか」などといった２変数の対応関係を調べます。ここでは、どちらが原因でどちらが結果かは問題にしません。

一方、回帰分析は、影響指標の変化が、成果指標とどのように関連しているかを調べます。例えば、「満足度が1ポイント上がると、生産性はどのくらい上がる傾向にあるか」といったことを分析します。影響指標の変化に伴う成果指標の変化を数値化しようとします。

結果の解釈の違い

• 相関分析：相関係数（r）は関係の強さと方向性を-1から1の間で表す
• 回帰分析：回帰係数（b）は影響指標が1単位変化したときの成果指標の変化量を表す

相関係数は、二つの変数の関係の強さと方向性を一つの数値で表現します。例えば、r=.80 は強い正の相関を示し、「一方の変数が高いとき、他方の変数も高い傾向が強い」ことを意味します。しかし、この数値は２変数の対応関係の強さを表すものであり、一方の変数が1単位変化したときに他方の変数がどれくらい変化するかという具体的なことは分かりません。

回帰係数は、影響指標の1単位の変化に対する成果指標の平均的な変化量を示します。例えば、満足度（1-5スケール）と生産性（1日あたりの生産量）の関係でb=10だった場合、「満足度が1ポイント上がると、生産量は平均して10単位増加する」という関連性を意味しています。しかし回帰係数は、「影響指標の得点が高いとき、成果指標の得点が高い傾向が頑健か」という、２変数がどの程度対応しているかの程度を考慮していません。

因果関係の扱い

• 相関分析：因果関係を想定しない。どちらが原因でどちらが結果かを区別しない。
• 回帰分析：因果関係を仮定する。影響指標が原因、成果指標が結果という関係を仮定する。

相関分析は、二つの変数が一緒に変動する傾向を見るだけであり、どちらが原因でどちらが結果かについては仮定しません。例えば、「満足度と生産性に正の相関がある」という結果が出ても、それが「満足度が高いから生産性が上がる」のか、「生産性が高いから満足度が上がる」のかは、相関分析だけでは判断できません。

一方、回帰分析では、影響指標を原因、成果指標を結果と仮定して、それらの関係を数学的にモデル化します。しかし、重要なのは、この仮定は分析者が行うものであり、回帰分析の結果自体が因果関係を保証するわけではないということです。例えば、「満足度が生産性に正の関連がある」という回帰分析の結果が出ても、それだけで「満足度を上げれば必ず生産性が上がる」と結論づけることはできません。

相関係数と回帰係数の違い

相関係数と回帰係数の違いは重要です。もう少し掘り下げておきましょう。

相関係数は２変数の対応関係の強さ、つまりデータが直線周りにどれだけ密集しているかを意味します。直線の傾きの大きさは考慮しません。

対して、回帰係数は直線の傾きを表します。回帰係数そのものはデータの分布の広がりを直接的には考慮しません[4]。

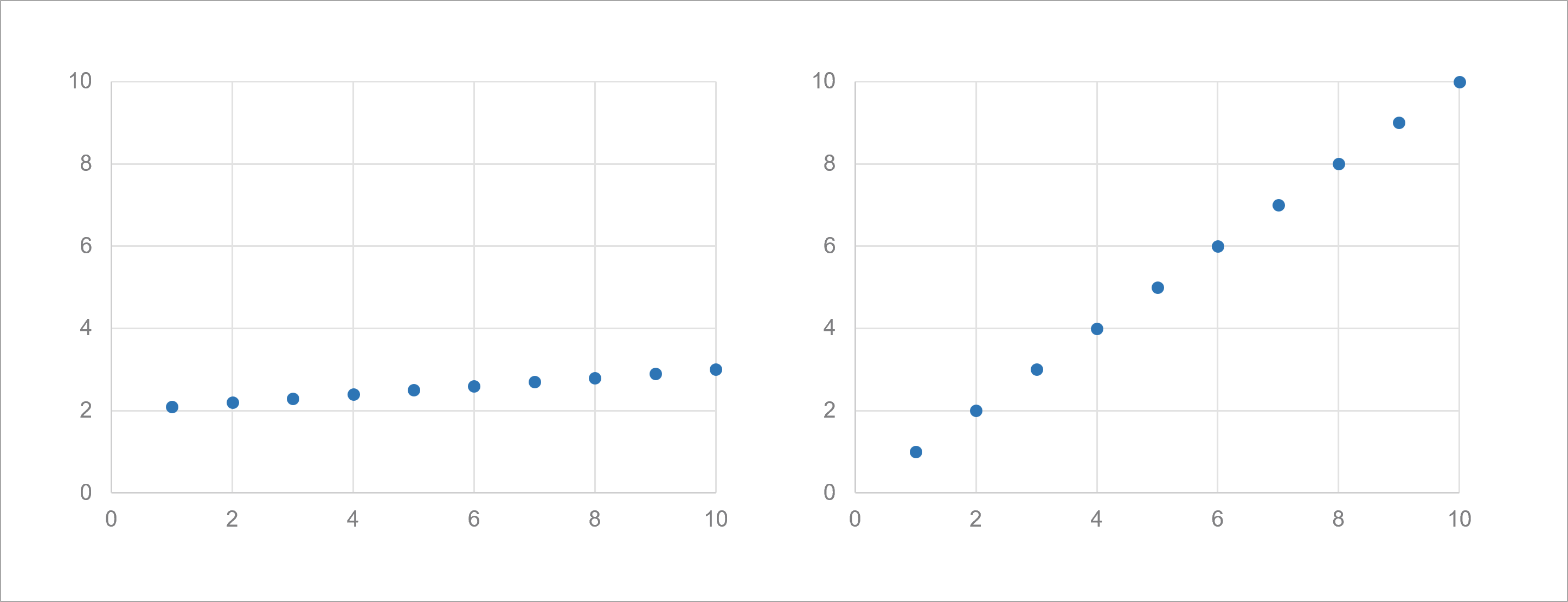
これらの違いは、実際のデータ分析において重要な意味を持ちます。次の図を見てください。

2つの散布図ともに、相関係数は同じで1.0です。しかし、左側は傾きが小さく、右側は傾きが大きくなっています。この場合、左側の回帰係数は小さく、右側は大きくなります。

このように、相関係数と回帰係数は異なる側面から関係性を捉えています。両方の指標を併せて考慮に入れることによって、データの特性を深く理解することができるでしょう。

相関分析と回帰分析の使い分け

相関分析と回帰分析の違いを理解したところで、それらをどのように使い分けると良いかを考えましょう。2つのシナリオと、それぞれに適した分析手法を紹介します。

シナリオ１．成果指標間の関連性、あるいは（因果関係を仮定しない）影響指標間の関連性を見たい場合：相関分析

複数の成果指標（例えば、満足度、組織コミットメント、離職意図）がどのように関連しているかを見たい場合や、複数の影響指標（例えば、リーダーシップ、支持的風土、能力開発機会）間の関連を把握したい場合などは、相関分析が適していると言えます。

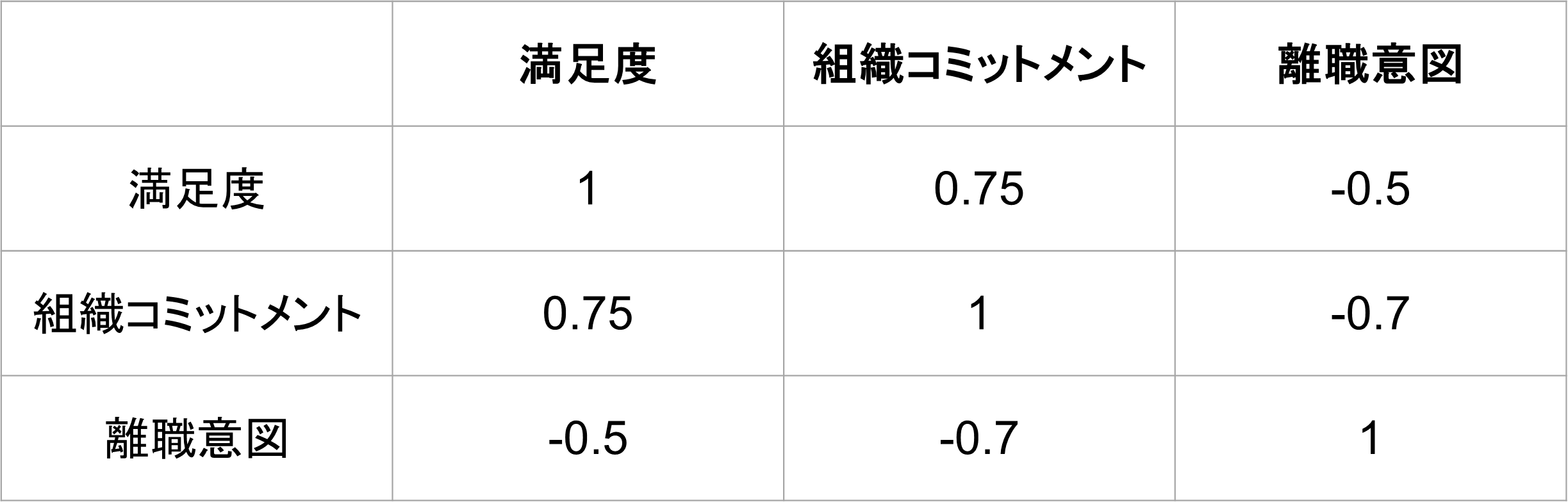
相関分析は複数の変数間の関連性を一度に概観するのが得意です。相関行列を作成することで、多くの変数間の関係を同時に確認できます。相関行列とは、複数の変数間の相関係数を行列形式で表したものです。

例えば、上記の相関行列は、次のような解釈が得られるでしょう。

• 満足度と組織コミットメントに強い正の相関がある（r=.75）
• 満足度と離職意図に中程度の負の相関がある（r=-.50）
• 組織コミットメントと離職意図に強い負の相関がある（r=-.70）

これらの成果指標が互いに密接に関連していることがわかります。特に、組織コミットメントが高い従業員は離職意図が低い傾向が強いことが示唆されています。

シナリオ２．特定の影響指標が成果指標とどの程度関連しているかを知りたい場合：回帰分析

回帰分析は、影響指標が成果指標と持つ関連性を数値で表すことができます。それによって、「影響指標が1単位変化したとき、成果指標はどの程度変化する傾向にあるか」という関係性を把握できます。

例えば、トレーニング時間（時間/月）を影響指標、従業員の生産性（単位/日）を成果指標として回帰分析を行ったとします。分析の結果、次のような回帰式が得られました。

生産性=50+2×トレーニング時間

この式における切片は50であり、トレーニング時間が0のとき、平均的な生産性は50単位/日となります。また、回帰係数は2であり、トレーニング時間が1時間増えると、平均して生産性が2単位/日だけ増える傾向があります。

さらに、決定係数が.30だったとすると、これは「トレーニング時間の違いが、生産性の違いの30%と関連している」と解釈できます。生産性の変動のうち30%は、トレーニング時間の違いと関連しているということです。残りの70%は、このモデルでは説明されていない他の要因や誤差によるものと考えられます。

具体例による違いの確認

最後に、架空の組織サーベイの例をもとに、これまでに述べてきた相関分析と回帰分析の違いを確認します。ある企業が従業員に対して行った組織サーベイで、次の概念をそれぞれ5段階で評価したとします。

• エンゲージメント（Y）
• リーダーシップ（X1）
• 支持的風土（X2）
• 能力開発機会（X3）

相関分析を行ったところ、次の結果が得られました。いずれも、エンゲージメントとの相関係数を表しています。

• リーダーシップ：r=.45
• 支持的風土：r=.52
• 能力開発機会：r=.38

これらの結果から、すべての影響指標がエンゲージメントと正の相関関係にあることがわかります。その中でも、支持的風土がエンゲージメントと最も強い関連性を持っています。逆に、能力開発機会の関連性が比較的弱いと言えます。

続いて、エンゲージメントを成果指標とし、他の3つを影響指標とした重回帰分析を行い、偏回帰係数として、リーダーシップが.25、支持的風土が.35、能力開発機会が.15、決定係数として.32という結果が得られたとします。

この結果に基づけば、モデル全体でエンゲージメントの変動の32%を説明できていることがわかります。支持的風土がエンゲージメントと最も強い関連を持っていると言えます。例えば、他の変数を一定に保った場合、支持的風土が1ポイント高い従業員は、平均してエンゲージメントが0.4ポイント高い傾向にあります。そして、リーダーシップも比較的強い関連がありますが、能力開発機会の関連は他の2つに比べて弱い傾向があります。

なお、相関係数と偏回帰係数の順序が若干異なっているのは、重回帰分析においては他の変数の影響を制御した上で各変数の関連を評価しているからです。

この例からも、相関分析と回帰分析はそれぞれ異なる視点からデータを解釈することができ、両者を組み合わせることで、豊かな洞察が得られることが分かるでしょう。

脚注

[1] 相関分析に関する詳細な解説は当社コラムをご確認ください。

[2] ただし、相関分析の結果は、因果関係を示すものではありません。また、この関係が非線形である可能性も考慮する必要があります。

[3] 決定係数は統計的な関連性を示すもので、必ずしも因果関係を意味するものではありません。

[4] 決定係数（R²）は、データが回帰直線の周りにどれだけ密集しているかを示します。R²が1に近いほど、データは回帰直線の周りに密集しています。

---

執筆者

伊達 洋駆　株式会社ビジネスリサーチラボ 代表取締役
神戸大学大学院経営学研究科 博士前期課程修了。修士（経営学）。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、組織サーベイや人事データ分析のサービスを提供している。著書に『60分でわかる！心理的安全性 超入門』（技術評論社）や『現場でよくある課題への処方箋 人と組織の行動科学』（すばる舎）、『越境学習入門 組織を強くする「冒険人材」の育て方』（共著；日本能率協会マネジメントセンター）などがある。2022年に「日本の人事部 HRアワード2022」書籍部門 最優秀賞を受賞。東京大学大学院情報学環 特任研究員を兼務。