2024年11月19日
関連性≠低スコア：回帰分析の適切な読み方
組織サーベイは、企業の現状を知る上で重要なツールです。しかし、その結果を理解することは、時として難しい課題となります。特に、統計分析の結果を適切に理解することは、統計学に慣れ親しんでいない人にとっては容易ではありません。
本コラムでは、組織サーベイの分析で時折見られる解釈の課題、特に回帰分析の結果の理解に関する点について解説します。
ある成果指標とある影響指標の間に有意な関連が認められたとき、「その影響指標のスコアが低い」と解釈されるケースがあります。この解釈がなぜ適切でないのか、そしてどのように考えることが望ましいのかを説明していきます。
正確な解釈の仕方や、実際に影響指標の値を検証する方法についても触れます。本コラムを通じて、組織サーベイの結果をより正確に理解するとともに、施策立案につなげられるようになることを狙います。
回帰分析とは何か
回帰分析は、変数間の関係を検討する手法の一つです[1]。組織サーベイの文脈では、例えば「満足度」（成果指標）と「リーダーシップ」（影響指標[2]）の関係を分析することができます。
回帰分析の結果、「有意な関連が認められた」というのは、成果指標と影響指標の間に統計的に意味のある関係があることを示しています。ここにおける「関連」の意味を正確に理解することが大事です。
「影響指標のスコアが低い」という解釈
組織サーベイの結果で、ある成果指標（例えば、満足度）とある影響指標（例えば、リーダーシップ）の間に有意な関連が認められたとします。この時、「リーダーシップのスコアが低い」と解釈する人がいるかもしれません。しかし、この解釈には注意が必要です。
この解釈の背後には、「成果指標と影響指標の間に関連があるということは、その影響指標に問題があるのではないか」という推論があるのではないでしょうか。「満足度とリーダーシップに関連があるということは、リーダーシップに課題があるのだろう」と考えるのです。
ところが、この解釈は必ずしも正確ではありません。なぜなら、回帰分析の結果は変数の間に関連があることを示しているだけで、その影響指標の実際の値（高いか低いか）を直接示すものではないからです。
値の低さとは異なる理由
回帰分析の計算式を参考に、なぜ「影響指標の値が低い」という解釈が適切ではないかを説明しましょう。回帰式は次のように表すことができます。
Y=a+bX+ε
ここで、Yは成果指標（例えば、満足度）、Xは影響指標（例えば、リーダーシップ）、aが切片（Xが0の時のYの値）、bが回帰係数（Xが1単位変化した時のYの変化量）、εが誤差項を指します。
回帰分析において「有意な関連が認められた」というのは、主にb（回帰係数）が統計的に有意であることを指します[3]。XとYの間に有意な関連があるということです[4]。
しかし、このbが有意であることは、Xの値（この場合、リーダーシップ）が高いか低いかを直接表すものではありません。bはXとYの間に関係があることを示しているだけなのです。
例えば、bが正の値で有意であった場合、それは「リーダーシップが高い人ほど、満足度も高い」ということを示しています。実際のリーダーシップのスコアが全体的に高いのか低いのかはわかりません。
リーダーシップのスコアが全体的に高い状況でも、それと満足度の間に正の関連が見られることはあり得ます。同様に、リーダーシップのスコアが全体的に低い状況でも、両者の間に正の関連が見られる可能性があります。
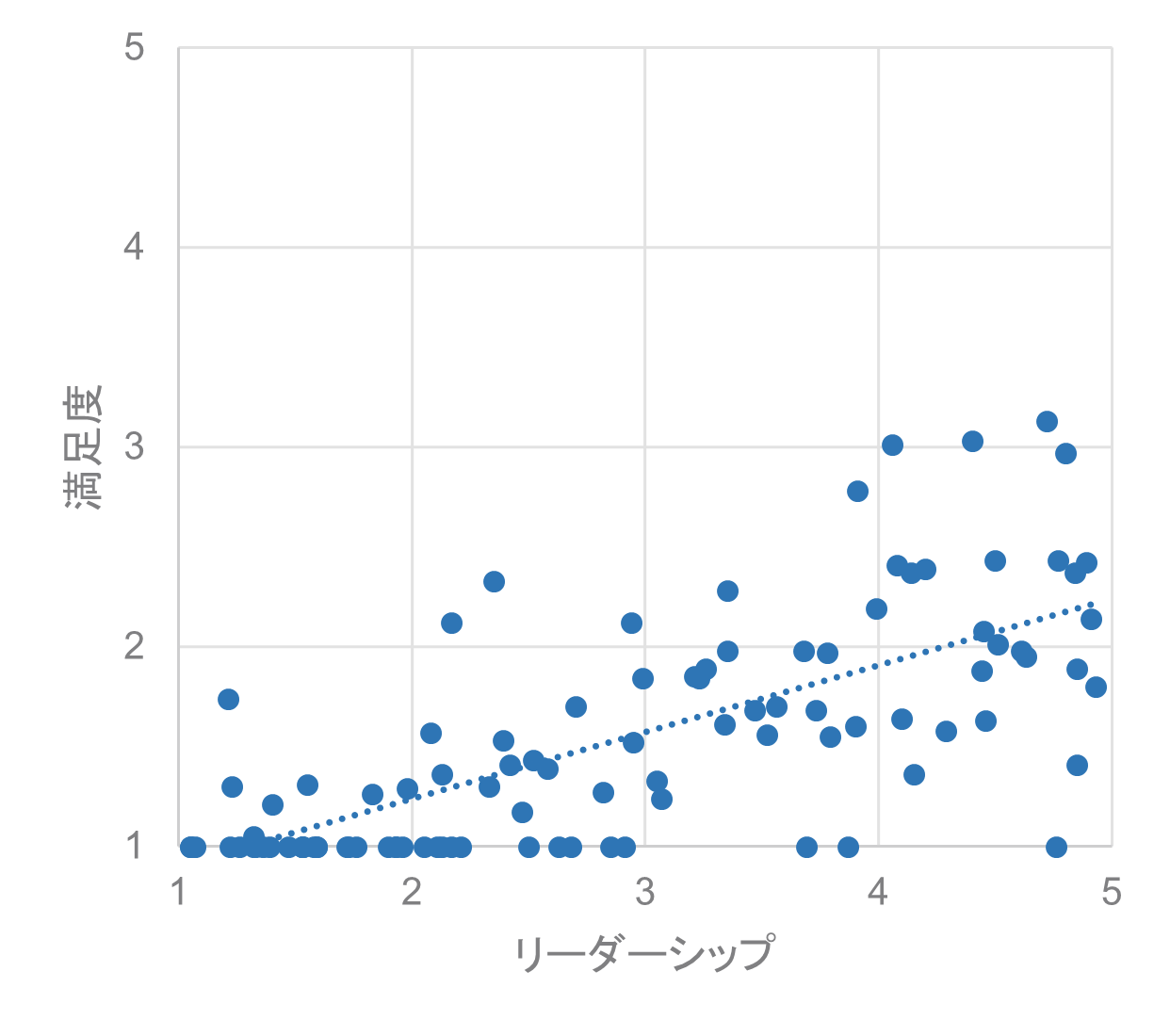
散布図と回帰直線
回帰分析の結果を直感的に理解するために、散布図と回帰直線が役立ちます。
散布図は、横軸に影響指標（例えば、リーダーシップ）、縦軸に成果指標（例えば、満足度）をとり、各データをプロットしたものです。
回帰直線は、これらのデータの傾向をよく表す直線です。回帰直線の傾きは回帰係数と一致します。
回帰分析で有意な関連が認められるとき、回帰直線はある程度の傾きを持っています。しかし、この傾きがあることと、影響指標の実際の値が高いか低いかは、別の問題です。
例えば、回帰直線が右上がりの場合（正の関連）、次のようなケースが考えられます。
- 影響指標が全体的に高い値に分布していて、なおかつ、成果指標と正の関連がある
- 影響指標が中程度の値に分布していて、成果指標と正の関連がある
- 影響指標が全体的に低い値に分布していて、それでも成果指標と正の関連がある
これらのケースはすべて、回帰分析では「有意な正の関連がある」という結果になります。回帰分析の結果だけでは、影響指標の実際の値を判断することはできないということです。
誤解が生まれる背景
成果指標と影響指標の関連を、影響指標の値の低さと受け止める誤解は、なぜ生じるのでしょうか。一つ大きな要因であると考えられるのは、ネガティブな解釈への偏りです。
組織サーベイを通じて、組織の問題点を見つけ出そうとする意識が強いと、ポジティブな解釈よりもネガティブな解釈に偏りがちです。「関連がある」ということを「問題がある」と受け止めてしまうのです。
これは人間のバイアスの現れであるとも考えられます。ネガティブな情報により注目してしまうのです。
しかし、例えば、リーダーシップと満足度の間に正の関連が見られた場合、それは「リーダーシップが優れているからこそ、満足度が高くなっている」という可能性も十分にあります。しかし、ネガティブな解釈に偏ると、こうした側面は見逃されてしまいます。
また、「関連がある」ということを「問題がある」と捉えると、実際には問題がない（既に十分に高い値にある）領域に不必要なリソースを投入することになりかねません。これは非効率な方法です。
影響指標の値を確認する方法
影響指標（例えば、リーダーシップ）の実際の値を知りたい場合、様々な方法があります。
記述統計量
記述統計量は、データの全体的な特徴を数値で表したものです。例えば、次のようなものがあります。
- 平均値：データの中心的な傾向を示す値
- 中央値：データを順に並べたときの中央の値
- 最小値：データの最も小さい値
- 最大値：データの最も大きい値
これらの値を確認することで、影響指標の全体的な傾向を把握することができます。例えば、平均値が高ければ、その影響指標は全体的に高い値にあると考えられます。
分散分析
分散分析は、複数のグループ間で平均値に有意な差があるかどうかを検定する手法です[5]。組織サーベイにおいては、部署や役職などの間で影響指標の平均値に差があるかを確認するのに用いることができます。
例えば、部署別にリーダーシップの分散分析を行い、有意な差が見られた場合、それは「部署によってリーダーシップスコアに差がある」ということを意味します。分散分析は、影響指標の全体的な値だけでなく、組織内のばらつきや差異を把握するのに役立ちます。
t検定
t検定は、二つのグループの平均値に有意な差があるかどうかを検定する手法です[6]。組織サーベイでは、例えば、男女間や管理職・それ以外などで影響指標の平均値に差があるかを確認するのに用いることができます。
t検定は、二つのグループ間の差異を統計的に確認するのに適しています。特定の属性や条件による影響指標の違いを把握することができます。
施策につなげるために
回帰分析の結果と影響指標の実際の値を両方確認することで、施策立案につながります。この過程を見ていきましょう。
回帰分析の結果は、成果指標と影響指標の関連性を示します。どの影響指標が成果指標と強い関連を持つかを特定できます。例えば、「リーダーシップ」が「満足度」と強い正の関連を持つことが分かったとします。
そうしたら、その影響指標（リーダーシップ）の実際の値を確認します。これには先ほど説明した記述統計量、分散分析、t検定などの方法を用いると良いでしょう。
これら二つの情報を組み合わせることで、次のような検討ができます。
- 関連性が強く、かつ実際の値が低い場合：その影響指標を改善することで成果指標の向上が期待できます。優先的に取り組むべき領域と言えるでしょう。例えば、リーダーシップのスコアが全体的に低く（例：5点満点中平均1点）、かつ満足度と強い正の関連がある場合、リーダーシップ研修やコーチングの導入などが効果的な施策となる可能性があります。
- 関連性が強く、かつ実際の値が高い場合：その影響指標は組織の強みとして捉えることができます。現状の高い値を維持しつつ、さらなる向上の余地がないか検討することも有効です。例えば、リーダーシップのスコアが全体的に高く（例：5点満点中平均8点）、かつ満足度と強い正の関連がある場合、現在のリーダーシップ育成の継続や、ベストプラクティスの共有などが有効な施策となるでしょう。
- 関連性が弱く、実際の値が低い場合：その影響指標の改善は成果指標の向上にあまり寄与しない可能性があります。例えば、在宅勤務日数と満足度の間に関連がなく、かつ低い値にある場合、直接的に満足度向上には寄与しないかもしれません。
- 関連性が弱く、実際の値が高い場合：その影響指標はすでに十分な値にあり、かつ成果指標との関連も弱いため、優先度は低いと判断できます。例えば、福利厚生の充実度が満足度と関連がなく、かつ高い値にある場合、現状維持でしょう。
このように、回帰分析の結果（関連性の強さ）と影響指標の実際の値を組み合わせて考えることで、より効果的に施策を検討することができます。それぞれの影響指標について、「関連性」と「実際の値」の両面から評価し、優先順位をつけていくと良いでしょう。
まとめ
組織サーベイの結果、特に回帰分析の解釈において「影響指標のスコアが低い」という誤解が生じることがあります。回帰分析で有意な関連が認められたということは、二つの変数間に統計的に意味のある関係があることを示しているだけで、影響指標の実際の値を直接示すものではありません。
この点を理解するためには、回帰式の意味や散布図と回帰直線の関係を把握することが有用です。また、ネガティブな解釈への偏りに注意を払い、より客観的かつ中立的な視点で結果を見る必要があります。
影響指標の実際の値を知りたい場合は、記述統計量、分散分析、t検定などの方法を用いることができます。これらの方法を活用することで、影響指標の全体的な傾向やグループ間の差異を捉えることができます。
さらに、回帰分析の結果と影響指標の実際の値を組み合わせて考えることで、効果的な施策立案につなげていけます。それぞれの指標について、「関連性」と「実際の値」の両面から評価し、優先順位をつけていくと良いでしょう。
データに基づいた意思決定の重要性が増す中、統計分析の結果を理解し、活用する能力は、ますます有用になっています。本コラムが、皆さんの組織におけるデータ活用の一助となれば幸いです。
脚注
[2] 本コラムでは「影響指標」という用語を用いていますが、これは必ずしも因果関係を表すものではありません。回帰分析は変数間の相関関係を示すものであり、因果関係を証明するものではありません。組織サーベイの結果を解釈する際は、この違いを念頭に置き、慎重に結論を導く必要があります。
[3] 本コラムでは理解しやすさを優先し、議論を単純化するため、決定係数の議論は取り上げていません。なお、コラムで扱っているような単回帰分析において決定係数は、標準化回帰係数の2乗と等しくなります。
[4] 本コラムにおいて、回帰分析における「有意な関連」とは、回帰係数bがp値を基準にして有意であることを指しています。しかし、p値のみで有意性を判断することにはリスクがあります。例えば、統計的に有意な結果が必ずしも重要な関連を意味するわけではなく、効果の大きさ（例えば、回帰係数の値や標準化係数）も確認する必要があるでしょう。
[5] 分散分析の詳細は当社コラムをご確認いただければと思います。
執筆者
伊達 洋駆 株式会社ビジネスリサーチラボ 代表取締役
神戸大学大学院経営学研究科 博士前期課程修了。修士（経営学）。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、組織サーベイや人事データ分析のサービスを提供している。著書に『60分でわかる！心理的安全性 超入門』（技術評論社）や『現場でよくある課題への処方箋 人と組織の行動科学』（すばる舎）、『越境学習入門 組織を強くする「冒険人材」の育て方』（共著；日本能率協会マネジメントセンター）などがある。2022年に「日本の人事部 HRアワード2022」書籍部門 最優秀賞を受賞。東京大学大学院情報学環 特任研究員を兼務。
