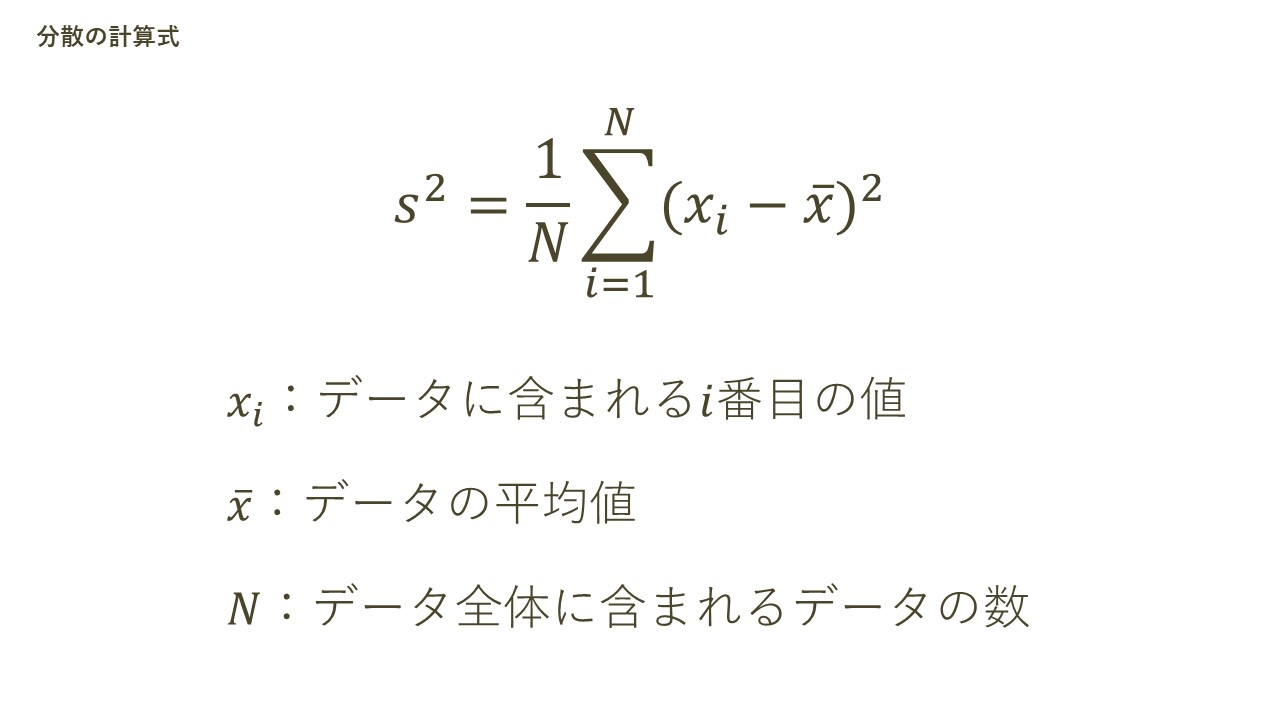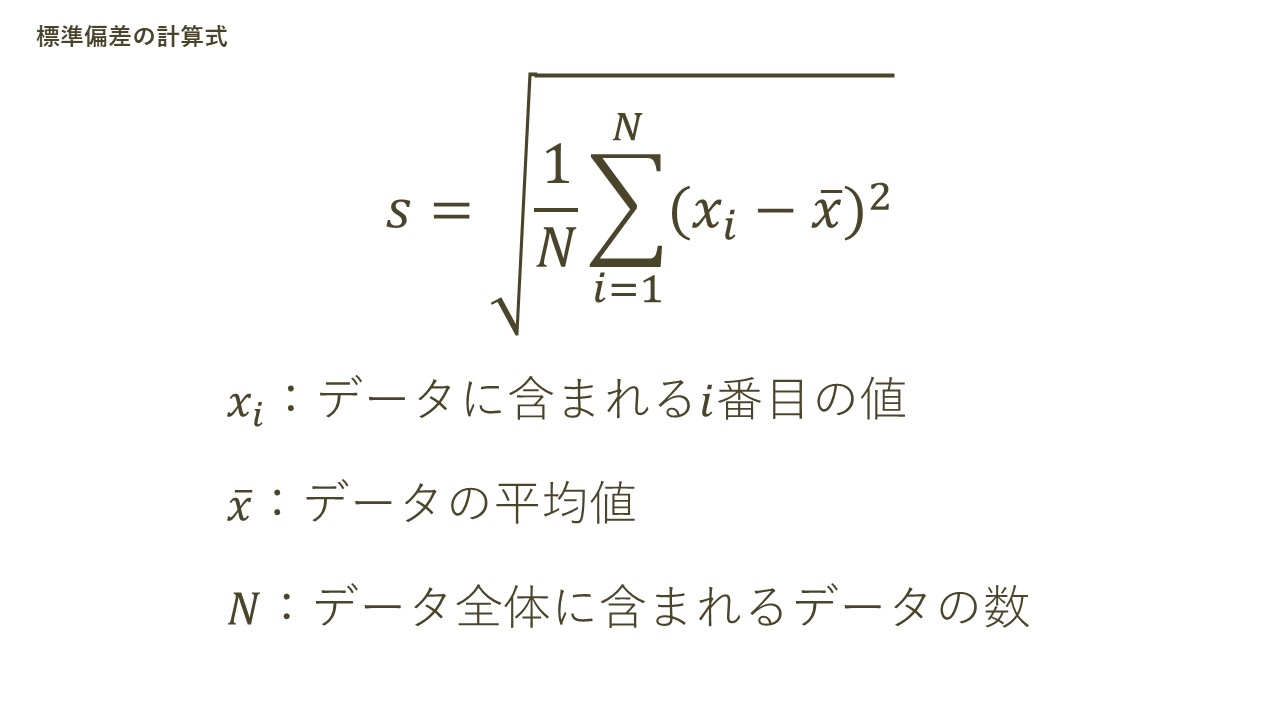組織サーベイや社内データ分析の結果を確認する際、平均値や最頻値などの代表値がよく使われますが、これだけではデータ全体の特徴を十分に把握することはできません。なぜなら代表値は、データがどのように散らばっているかを示していないためです。

例えば、従業員のエンゲージメントについて、同じ程度の平均値を持つ部署であっても、皆近い点数なのか、あるいは高得点者から低得点者まで混在しているのか、得点のばらつきは異なることがあり得ます。また、こうした違いを見逃すと、対策の有効性が下がる可能性もあるのです。

したがって、データ全体の傾向を理解するためには、代表値だけでなく、回答のばらつき・散らばり具合を表す指標にも目を向けることが重要です。本コラムでは、その指標である「散布度」について解説しながら、実務で活用する際のポイントも併せて紹介していきます。

1章：散布度を踏まえた実態把握の例

データの散らばりを確認できる；組織サーベイを仮想例に

手元のデータ全体の特徴を概観する場合、平均値をはじめとした「代表値」によって判断することが多くあります^[1]。しかし、そうした特定の値だけでは、データの特徴を適切につかみ切れません。次のような例を考えてみます。

ある会社で、従業員のエンゲージメントの状態を把握するため、部署Aに対して組織サーベイを実施したとします。その仮想の結果を、次のような図に表してみます。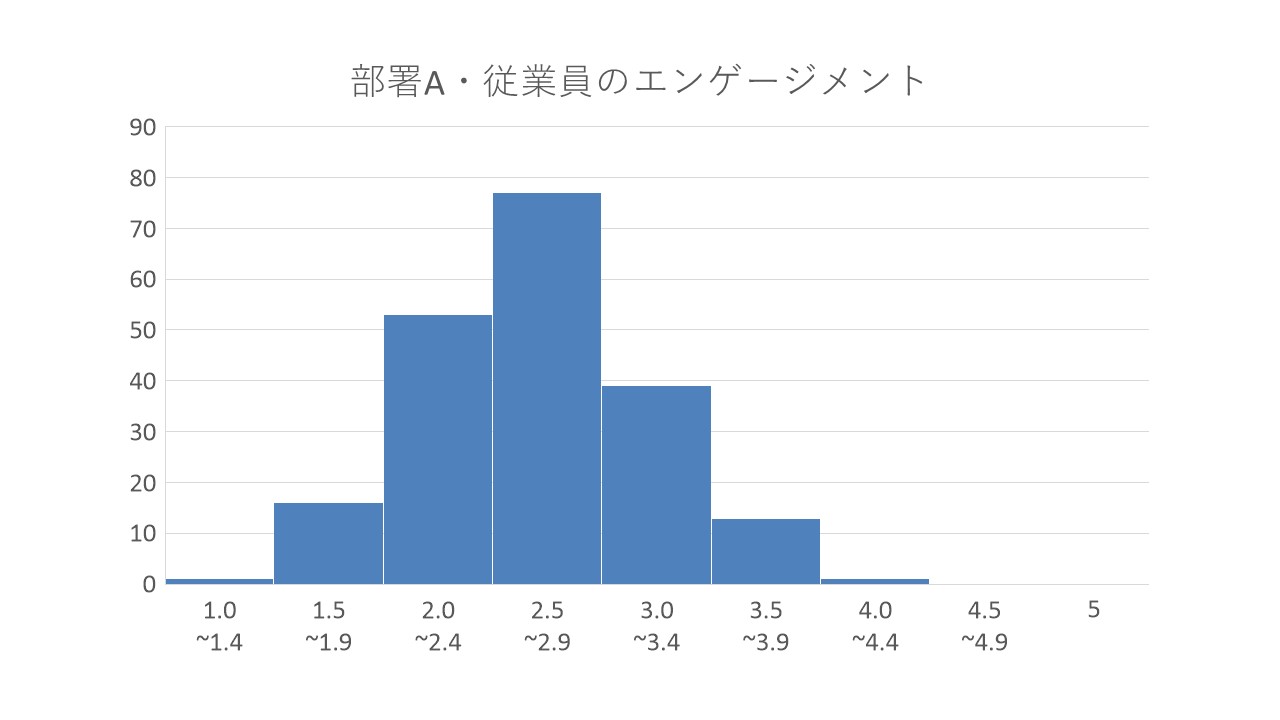

上記のグラフはヒストグラムといい、回答をいくつかの水準に分け、それぞれの水準に該当する回答者数が何名ずついたのかを集計したものです。このように、組織サーベイを実施すると、比較的高い点数の高い従業員から低い従業員まで、回答の得点は一定の散らばりがあるものです。

しかし、たとえば平均値など代表値は、こうしたデータの散らばりを反映しているわけではありません。そのため、データ全体で、各回答が散らばっている度合いを表すために、散布度と呼ばれる指標が使われるのです。

平均値だけでは見落とす実態に気づける

ここからは、先ほどの仮想例を引き継いで、散布度を確認することで得られるメリットについて、具体的に確認していきます。エンゲージメントの組織サーベイを実施したと仮定し、部署Aと部署Bのそれぞれの結果が以下のようになったとします。

• 部署A：平均2.6点/5点、標準偏差5
• 部署B：平均3点/5点、標準偏差1.9

平均点だけを見ると、部署Bの方がエンゲージメントの得点が高いため、部署Bは部署Aに比べてエンゲージメントの問題が少ないと判断するかもしれません。ここでポイントになるのが、上記の結果として平均点の隣に示された「標準偏差」です。詳細は後述しますが、標準偏差は今回のテーマである散布度の1つです。

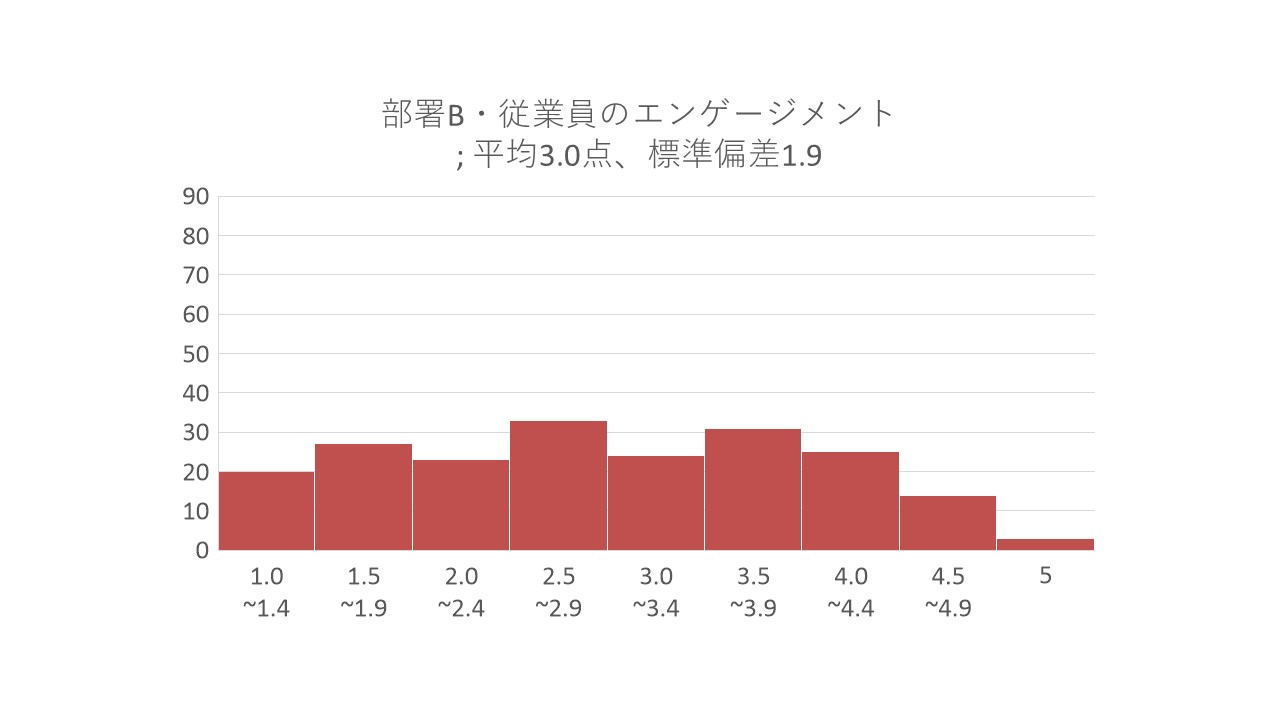
標準偏差を比べると、部署Bの方が幾分大きくなっています。この結果を比べるために、上記の結果を満たす仮想データを生成し、ヒストグラムによって比較してみます。部署Aの結果は、先ほどのヒストグラムが反映しています。部署Bのヒストグラムが、以下のようになっていたとします。

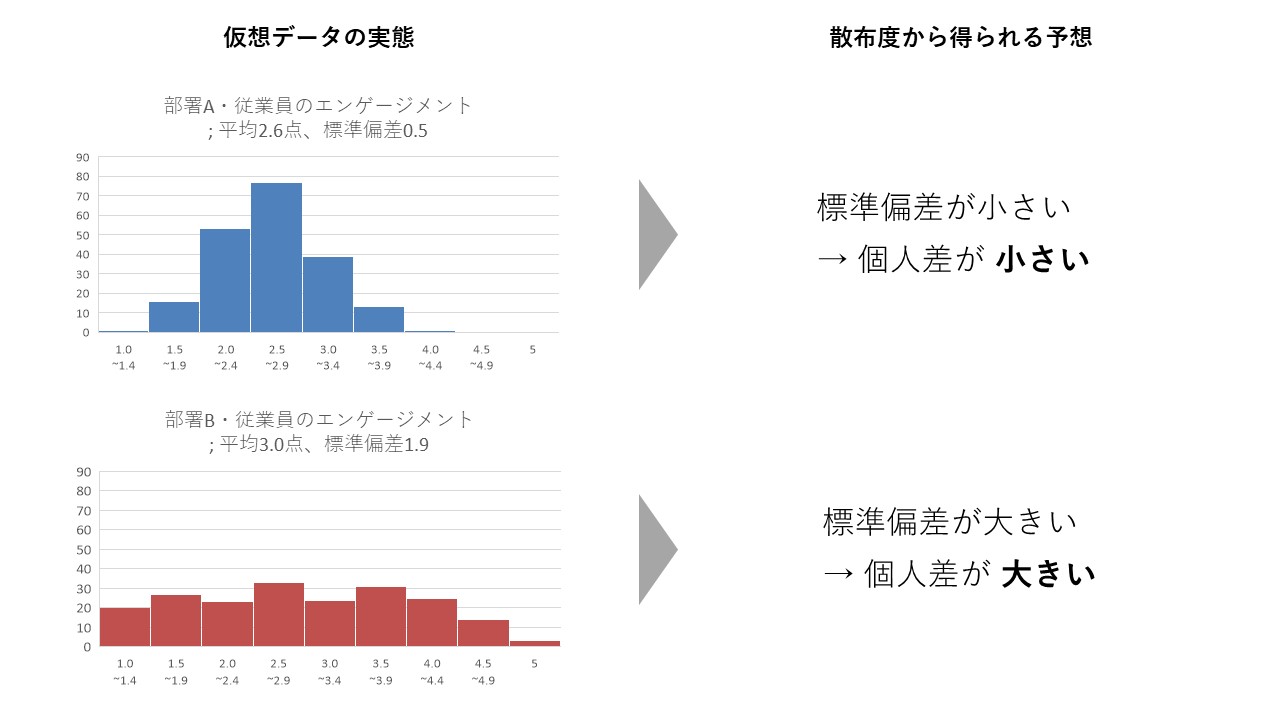
部署Bの結果は、エンゲージメントレベルの高い従業員から、中程度の従業員、あるいは、非常に低い従業員まで、満遍なく在籍していることが分かります。言い換えてみると、部署全体で、エンゲージメントの個人差が大きいと言えます。そこで、部署Aと部署Bのヒストグラムを、以下のように対比しました。

部署Aを再確認してみると、平均点と同程度のエンゲージメントである従業員が多く、個人差が部署Bよりも小さいことが分かります。逆に部署Bは、平均点こそ部署Aより高いものの、実は部署Aにはいないような、エンゲージメントが非常に低い従業員が在籍していることも確認できます。こうした詳細な情報は、ローデータやヒストグラムをつぶさに確認して分かることですが、散布度を確認することでも大まかに予想できるのです。

ここまで、散布度を確認するメリットを紹介してきました。これらは裏を返すと、散布度を確認していない場合は、実態を見誤ったり、施策の効果を最大化できないリスクがあるとも言えます。「馴染みがあり、解釈しやすい代表値さえ確認しておけばよいのではないか」と考えるかもしれませんが、併せて散布度を確認することも重要なのです。

２章：散布度にはどのようなものがあるか

範囲

では、実際にはどのような散布度の指標があるでしょう。ここでは、人事データ分析とのかかわりが深い指標を紹介します^[2]。

まず紹介するのは、範囲と呼ばれる指標で、これは最大値と最小値の差によって表されます。たとえば、組織サーベイなどで使われる心理尺度の多くは、自分の状態や考えなどを5段階で回答を求めます。そうした調査で、得られた回答に1点と5点があれば、その範囲は5－1＝4となります。あるいは、2点から4点の範囲に回答が収まる可能性もあり、その場合の範囲は4－2＝2となります。このように、データの最大値と最小値から範囲を算出して確認することで、どの程度の範囲に回答が収まるのか、という初歩的な散布度を確認することができます。

分散

次に、分散です。これは、代表値である平均を土台として算出されるものです。具体的には、以下の数式で表されます。

上記の数式に沿って、分散の計算方法を確認します。まず、左辺のsの二乗は、分散を表す統計記号です。続いて、その分散を算出するための右辺の計算について、それぞれの処理が持つ意味と共に紹介していきます。

初めに、データに含まれる各回答者のデータxからデータの平均値を引き、その値を二乗します。この処理は、各値が平均値からどのくらい離れているのか、という距離を算出する目的があります。次に、この計算をデータに含まれるすべての値で実施し、それらを足し合わせます。これにより、平均値を基準にした各値の距離の情報を、データ全体で集約することができます。

そして、その足し合わせた値をデータ全体に含まれるデータの数で割ります。これにより、「データ数が多いほど、足し合わせた値が大きくなる」問題を取り除きます。この一連の手続きによって算出されるのが、分散と呼ばれる散布度です。

上記の手続きのうち、「二乗」する手続きに疑問を持つかもしれません。この手続きがなぜ必要なのか、という点を掘り下げてみていきましょう。

データの各値から平均値を引く処理において、平均値より大きなデータの計算では差が正の値になりますが、平均値よりも低いデータの計算では、差は負の値になります。続けて、これらを算出した後で、散布度として1つの値へ集約するために、全ての値を足し合わせるという計算を行います。

このとき、距離に関する正負を考慮せずそのまま足し合わせてしまうと、プラスとマイナスで打ち消し合ってしまい、距離の情報を正しく反映できなくなります。そこで、二乗する処理を加えることにより負の値を正の値にして、こうした正負の問題に対処しているのです。

標準偏差

最後に紹介するのは、データがどの程度ばらついているかの散布度を表す指標としてもっとも用いられる、標準偏差です。これは、上記の分散を利用することで算出されます。具体的には、以下の数式です。

左辺sは、標準偏差を表す統計記号です。また、右辺は先述した分散について、その平方根をとるという処理を加えています。分散を算出する過程では、二乗という得点の処理が行われることを紹介しました。ただし、その二乗された状態のままでは、データ全体の分布を端的という目的には、いささか難解です。そのため、分散を元のデータと同じ水準に戻すことで得られる指標、と理解すると良いでしょう。

標準偏差は、データ全体の分布の特徴を理解するうえで、大変便利な性質を持っています。その特徴とは、平均点を中心として、標準偏差の大小一つ分の範囲にデータ全体の68.3％が、標準偏差の大小二つ分の範囲には95.5％が収まる、という性質です。

例えば、前述の仮想データでは、部署Aの平均値が2.6、標準偏差が0.5となっていました。そこで、平均点から大小1つ分、および大小2つ分の範囲を計算すると以下のようになります。

• 標準偏差1つ分：2.1点～3.1点
• 標準偏差2つ分：1.1点～3.6点

後述するように、この特徴は正規分布している場合に限るものですが、上記の範囲に理論上は回答者の約7割、あるいは、約9割が収まっていると確認することができるのです。平均値と標準偏差を確認することにより、別途作図をせずとも分布を大まかに概観できることを考えると、利便性が高い特徴といえるでしょう。

3章：実務で使用する際のポイント

分散と標準偏差の使いわけ

最後に、実務上のデータ分析の際に散布度を確認する際のポイントを確認していきます。まず、分散と標準偏差の使い分けについてです。

上記のように、分散と標準偏差は非常に近しい関係性にありますが、両者は厳密に使い分けられています。実際、人事データ分析の結果を解釈する場合、分散それ自体を解釈することは多くはありません。

その理由は、上述のように分散という値の意味が難解であり、便利な特徴も備えている標準偏差へ変換した方が、データ全体の特徴を解釈しやすいためです。そのため、公開されているデータを理解するという目的や、データ分析を直接実施する立場にない場合には、標準偏差の意味合いを理解しておけば問題ないでしょう。

一方で分散は、推測統計などの多くの計算に用いられる値でもあります。そのため、今後自分でデータ分析を担当する立場になると予想される場合は、用語と算出法を押さえておくと良いでしょう。

正規分布であるかの確認

続いて、データ全体が「正規分布」といえるかどうかを確認することが重要であることを掘り下げます。まず前提として、正規分布とはどのような分布のことを指すのかを紹介します。

本コラムの冒頭で示した例は仮想のデータですが、ソフトウェアにより正規分布となるように設定しています。上記の例のように、データの分布が、指標の取りうる得点の幅の真ん中付近に多くのデータが集まり、そこから離れるほどデータの数が少なくなるような分布を、正規分布と呼びます。

では、なぜデータ全体が正規分布であるかを確認する必要性があるのでしょう。それは、散布度から推測したデータの概要が、実際のデータ全体の特徴と一致していない可能性があるためです。具体例として、データが正規分布をしていない場合、標準偏差に備わっていた、平均値から標準偏差1つ分の範囲に約７割のデータが収まる、という性質が成り立たなくなります。

いくつかの質問や調査内容によっては、ある指標のデータが正規分布の特徴を満たさないことがあることもたびたび確認されます。例えば、日本の年収の分布などは、一部の富裕層を除いて、少額で生活する人が大半である場合です。他にも、会社内での表彰回数や、不正行為の目撃など、発生頻度がまれである経験も、その回答の分布には偏りが発生することが予想されます。

散布度をうまく活用するため、まずはデータが正規分布しているか確認する習慣をつけると良いでしょう。手元のデータが正規分布になっているかどうかを確認する方法として、簡便な方法の1つが、代表値を確認することです^[3]。詳細は割愛しますが、データ全体が正規分布になっている場合は、平均・中央値・最頻値が、ほぼ同じ値をとることが分かっています。逆に、値が異なる場合は正規分布になっていない可能性があるため、解釈に注意が必要です。

また、間接的な方法としては、どのような内容に関するデータであるかを確認することです。上記のように、回答が正規分布しづらい調査の内容であるかどうかは、前例を確認することで予想ができます。調査内容が正規分布になりやすいかどうかという点を、その前例と併せて確認しておくことで、新たに取得したデータについても注意しながら確認する事ができます。

ここまで見てきたように、手元のデータ全体の特徴を理解するうえで、代表値だけではなく散布度を併せて確認する必要があります。しかし、散布度をそれだけで確認することにも、実はリスクがあるということです。より発展的な分析や、分析結果を踏まえた施策の精度も高めるためにも、両者を併せて確認することで、データを適切に概観することが大切です。

脚注

^[1] 代表値とは何か、あるいは、代表値を扱うときの注意点などは、当社の別コラムでまとめております。適宜参考ください；代表値とは何か：データを適切に概観するために

^[2] 本章の解説は、以下の資料に基づいています。数理的な原理など、より詳細な解説については、原典をご確認ください；南風原 朝和（2002）.　心理統計学の基礎 総合的理解のために（有斐閣アルマ）　pp17-41

^[3] より直接的には、推測統計を用いて確認する方法もあります。詳細は、以下のコラムが参考になります；5歪度と尖度｜Bell Curve「統計学WEB」