本コラムは、主に企業の人事担当者に向けて、t値からt分布を用いてp値を算出するプロセスを解説するものです[1]。そのことによって、「統計的に有意」が意味するところをより正確に理解できるようになります。

なぜ、本コラムの内容が必要かというと、「統計的に有意」の意味を誤解しているケースも少なくないからです。例えば、p値が0.05未満であることをもって「差がある」と断定したり、逆にp値が0.05以上であることをもって「差がない」と結論づけたりするのは、統計的推論の本質を見誤っています。

p値は、観測されたデータが帰無仮説（差がないという仮説）と矛盾する程度を表す指標に過ぎず、直接的に差の有無や大きさを示すものではありません。

p値について理解を深めることで、人事領域におけるデータドリブンな意思決定をより洗練されたものにすることができます。本コラムでは、エンゲージメントスコアの比較を例に、各ステップの意味と重要性を解説していきます。

エンゲージメントスコアの例

具体的な例を設定しましょう。ある会社の営業部と開発部のエンゲージメントスコアを比較する場面を想像してください。

• 営業部のエンゲージメントスコア平均：75点
• 開発部のエンゲージメントスコア平均：72点
• 営業部の従業員数：120人
• 開発部の従業員数：100人
• 営業部のスコアの標準偏差：9点
• 開発部のスコアの標準偏差：11点

営業部のスコアが開発部より3点高いということがわかります。しかし、この差は統計的に意味のあるものでしょうか。これを判断するために、t検定という手法を用います。

t検定においてはt値を算出します。t値は、2つのグループ間の差を標準化した指標です。観測された差がどれくらい大きいのかを、データのばらつきを考慮して表現するものです。t値の計算式は次のように表すことができます。

t=(₁-₂)/√(s²₁/n₁+s²₂/n₂)

この式において、₁と₂はそれぞれのグループの平均値、s²₁とs²₂はそれぞれのグループの分散（標準偏差の二乗）、n₁とn₂はそれぞれのグループのサンプルサイズを指します。式をもとにt値を計算してみましょう。

t=(75-72)/√((9²/120)+(11²/100))

=3/√(0.675+1.21)

=3/√1.885

≈2.186

この約2.186という値が、営業部と開発部のエンゲージメントスコアの差を表すt値となります。

また、自由度も計算しておきましょう。2つの独立したグループを比較する場合の自由度は次の式で導き出すことができます[2]。

自由度=n₁+n₂-2

今回の例では「120+100-2=218」となります。

これで、t値が2.186、自由度が218であることがわかりました。これらの値を用いてp値を算出する過程を見ていきます。

t分布

p値を求めるためには、t分布という確率分布を理解する必要があります。それに先立って、確率分布とは何かを説明しましょう。確率分布とは、確率変数（ランダムな事象の結果を数値で表したもの）が取り得る値とその確率の関係を表したものです。ある事象がどのような確率で起こるかを表す数学的なモデルです。

サイコロを振る場合を考えてみましょう。サイコロの目（1から6）が確率変数で、それぞれの目が出る確率（それぞれ1/6）がその確率分布となります。これは離散的な確率分布の例ですが、t分布は連続的な確率分布の一つです。

t分布は、小標本（サンプルサイズが小さい場合）における平均値の分布を表す確率分布です。正規分布に従う母集団から抽出された標本の平均値が、母平均からどのくらい離れているかを表現するための分布として用いられます。

t分布にはいくつかの特徴があります。

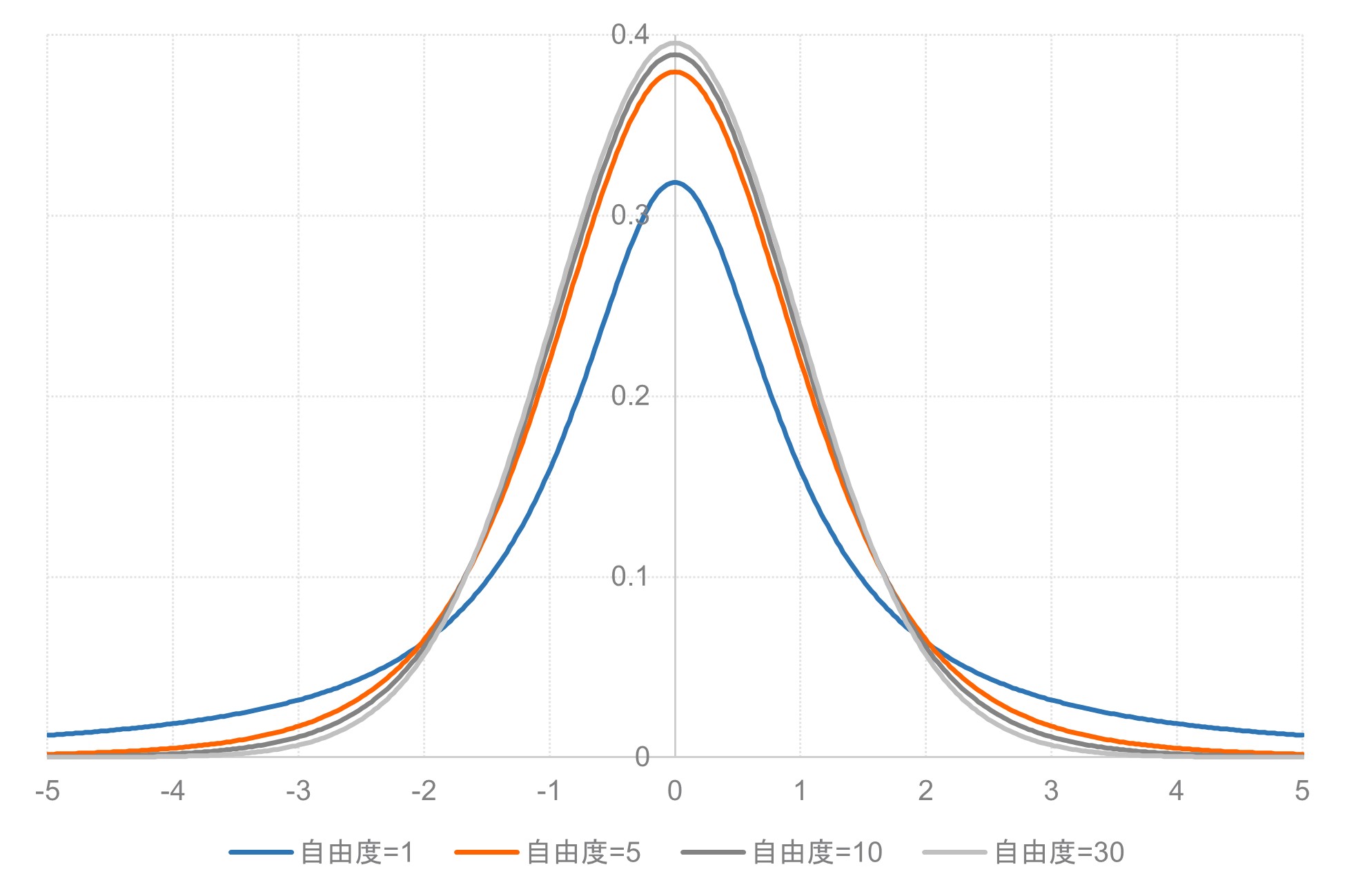
まず、t分布は左右対称の釣鐘型をしています。これは、中心を軸に左右対称の形をしていることを意味し、正の値と負の値が同じ確率で出現することを指しています。

次に、t分布の形状は自由度によって変わります。自由度が小さいほど、分布の裾が重くなります。「裾が重くなる」とは、分布の中心から離れた値が出現する確率が高くなることを意味します。サンプルサイズが小さいほど、極端な値が観測される可能性が相対的に高くなることを反映しています。

自由度が大きくなるにつれて、t分布は標準正規分布に近づいていきます。サンプルサイズが大きくなるほど、推定の精度が向上し、極端な値が出現する確率が低くなることを表しています。

このことは、中心極限定理と関連しています。中心極限定理は、独立した多数の確率変数の和（または平均）の分布が、サンプルサイズが大きくなるにつれて正規分布に近づくという定理です。サンプルサイズが大きくなれば、どのような分布からデータを抽出しても、その標本平均の分布は正規分布に近似するようになります。

そして、t分布の平均は常に0です。これは、t値が「標準化された差」であることと関係しています。t値は、観測された差を標準誤差で割ったものです。帰無仮説（差がないという仮説）が真である場合、標準化された差の期待値は0となります。

もし本当に差がないのであれば、標準化された差（t値）は平均的に0になるはずだ、ということです。これは、帰無仮説のもとでは、正の差と負の差が同じ確率で起こることを意味しています。2つのグループ間に差がないのであれば、一方のグループの平均が他方より大きくなる確率と、小さくなる確率は等しいはずです。

t分布は、帰無仮説のもとでのt値の理論的な分布を表現しています。要するに、t分布は、「もし本当に差がないとしたら、t値がどのような分布になるか」を意味しています。これは非常に重要な観点です。というのも、t分布という理論的な分布があるからこそ、観測されたt値がどれくらい「珍しい」値なのかを判断できるからです。

t分布によって、実際に観測されたt値が、帰無仮説のもとでどれくらい起こりやすい（あるいは起こりにくい）値なのかを評価することができます。観測されたt値が、t分布の中で非常に起こりにくい値（つまり、分布の裾の方に位置する値）であれば、それは帰無仮説と矛盾する証拠となり得ます。この「起こりにくさ」を定量化したものが、後で説明するp値となります。

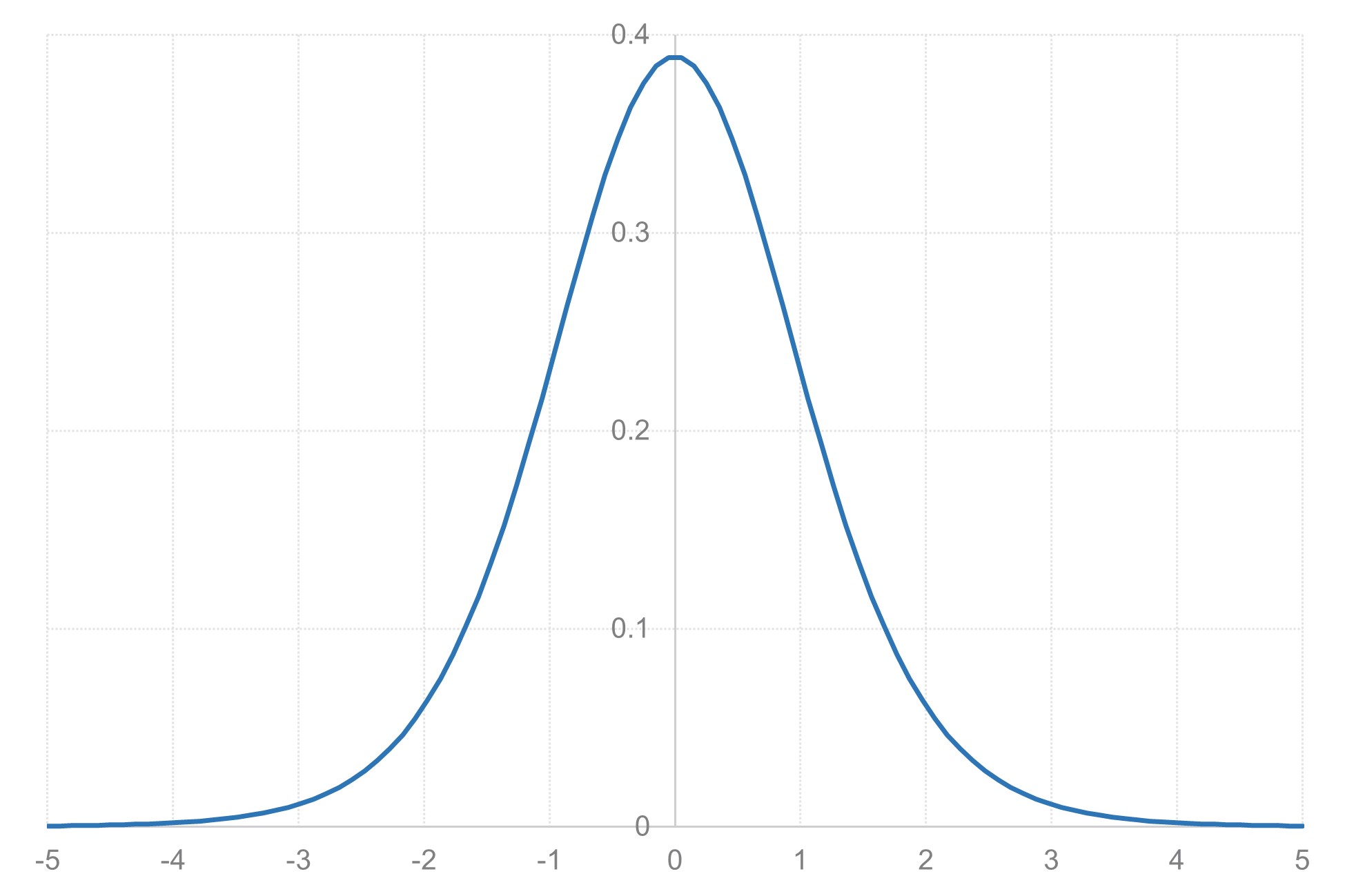
確率密度関数

続いて、t分布の確率密度関数について理解すると良いでしょう。確率密度関数とは、連続的な確率変数の分布を表す関数です。確率密度関数は、各点での「確率の密度」を表します。ある値の近傍で確率がどれくらい集中しているかを示します。

「確率の密度」という概念は、少し理解しにくいかもしれません。比喩として、人口密度を考えてみましょう。ある地域の人口密度が高いということは、その地域に多くの人が集中して住んでいることを意味します。同様に、確率密度が高いということは、その値の周辺で確率が集中していることを意味します[3]。

確率密度関数自体は確率ではありませんが、確率密度関数を積分することで、ある範囲の確率を求めることができます。積分については、数学で学んだことがあると思いますが、非常に簡単に言えば「面積を求める」操作です。確率密度関数のグラフの下の面積が確率を表すということです。

例えば、ある区間の確率を求めたい場合、その区間での確率密度関数の積分を計算します。これは、その区間でのグラフの下の面積を求めることに相当します。この面積が、その区間に値が入る確率を指しています。

t分布の確率密度関数は次のように表すことができます。

f(t)=[Γ((ν+1)/2)/(√(νπ)*Γ(ν/2))]*(1+t²/ν)^(-(ν+1)/2)

この式におけるν（ニュー）は自由度、Γ（ガンマ）はガンマ関数、π（パイ）は円周率です。複雑な数式が出てきたことで、憂鬱な気分になった人もいるかもしれません。しかし、構成要素の意味するところを追いかければ、式の表したいことが見えてきます。

• Γ((ν+1)/2)とΓ(ν/2)において、ガンマ関数が用いられています。ガンマ関数は、階乗を連続的に拡張したものです。これらの項は、分布の形状を調整する役割を果たします。自由度に応じて分布の形を適切に変化させる働きをします。自由度が小さい場合は分布の裾が重くなり、大きい場合は正規分布に近づくように、これらの項が分布の形を調整しています。
• √(νπ)という項は、確率密度関数を正規化し、全体の面積が1になるようにしています。確率密度関数の全体の面積は1でなければならないという制約があり、この項はその制約を満たすための調整を行っています。すべての可能な結果の確率の合計は1（100%）でなければなりません。連続的な確率分布の場合、この「合計」は積分によって行われます。したがって、確率密度関数を全区間で積分した結果が1になるように調整する必要があります。
• (1+t²/ν)^(-(ν+1)/2)という項は、t分布の特徴的な形状を生み出します。t²/νが小さいほど（tが0に近いほど）この値は大きくなり、逆にt²/νが大きいほど（tの絶対値が大きいほど）この値は小さくなります。tの値が0に近いほど確率密度が高くなり、tの絶対値が大きくなるほど確率密度が小さくなりますが、その減少の仕方が正規分布よりもゆるやかになります。これによって、t分布の中心部分が高く、裾が重い形状が作られます。

確率密度関数は、t値が取り得る各値に対して、その値が出現する相対的な確率を与えます。すなわち、ある特定のt値が観測される「可能性の高さ」を表現しています。ただし、前述の通り、確率密度関数の値自体は確率ではありません。確率を得るためには、確率密度関数を積分する必要があります。

累積分布関数

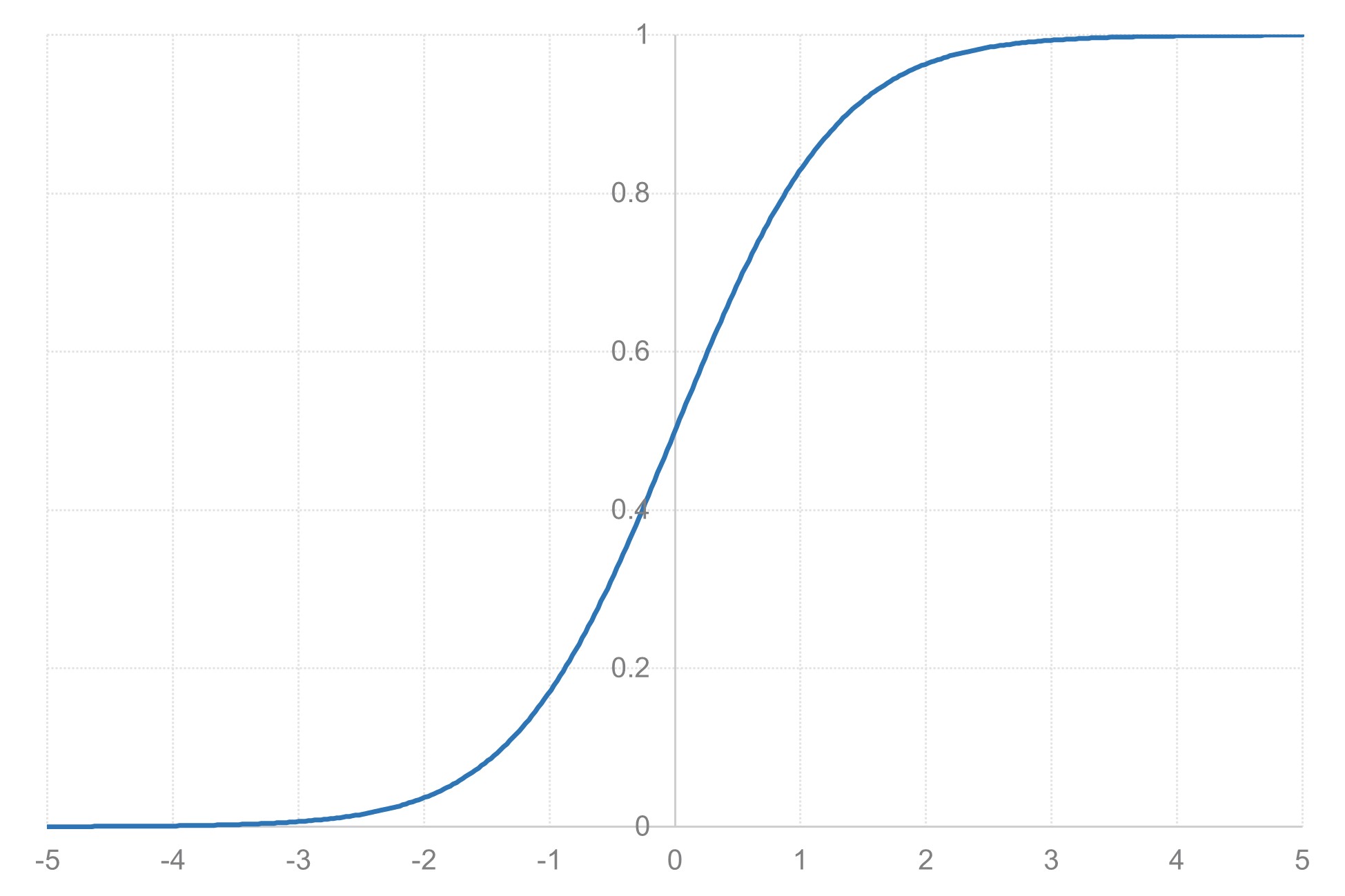
確率密度関数を理解したところで、次は累積分布関数について説明します。累積分布関数とは、ある値以下となる確率を表す関数です。確率変数が特定の値以下となる確率を、その値の関数として表したものです。

累積分布関数についてイメージをするために、身長の分布を考えてみましょう。身長170cm以下の人の割合を知りたい場合、身長の累積分布関数を使用することができます。CDFを累積分布関数（Cumulative Distribution Function）の略記として、CDF(170)は身長が170cm以下である確率を返します。

累積分布関数は、先ほどの確率密度関数と密接な関係にあります。確率密度関数が各点での確率の「密度」を表すのに対し、累積分布関数はある点までの確率を「積算」したものです。「密度」と「積算」の関係は、（確率密度関数を説明した際の例を引き継げば）人口密度と総人口の関係に似ています。人口密度は各地点での人の集中度を表し、それを地域全体で合計すると総人口になります。

例えば、ある都市の人口密度が1平方キロメートルあたり1000人で、その都市の面積が100平方キロメートルだとすると、都市の総人口は1000*100=100000人となります。これは、人口密度（確率密度関数に相当）を都市全体（全確率空間に相当）で合計（積分）した結果です。

同様に、確率密度関数をある範囲で積分すると、その範囲の確率（累積分布関数の値の差）が得られます。例えば、t分布において、t値が-1から1の間に入る確率を知りたい場合、この範囲でt分布の確率密度関数を積分します。

要するに、累積分布関数は確率密度関数を積分することで得られるということです。積分は、面積を求める操作であり、確率密度関数のグラフの下の面積が確率を表します。具体的には、-∞から任意の点xまでの確率密度関数の積分が、その点xでの累積分布関数の値となります。これは、xまでのすべての確率を足し合わせていることを意味します[4]。

t分布の累積分布関数は、次のように定義されます。

F(t)=P(T≦t)

F(t)は累積分布関数、P(T ≤ t)は、確率変数Tがt以下となる確率を指します。ここでも式の構成要素を把握すれば、式の意味するところが見えてきます。

• F(t)は累積分布関数そのものを表します。tという値が与えられたとき、F(t)はその値以下となる確率を返します。ここでのtは、一般的な変数を表しており、必ずしもt値のみを意味するわけではありません。しかし、t分布を扱う文脈では、多くの場合tはt値となります。
• P( )というのは確率を表す記号です。括弧内の条件が成立する確率を意味します。例えば、P(X＜5)は、確率変数Xが5より小さくなる確率ということです。
• Tというのが確率変数です。この場合、t分布に従う確率変数を表します。確率変数とは、ランダムな事象の結果を数値で表したものです。例えば、サイコロを振った結果や、ある人の身長などが確率変数となります。Tは理論上あり得るすべてのt値を表現しており、具体的な一つの値ではなく、可能性のある値の集合を意味しています。

この式は「t分布に従う確率変数Tが、与えられた値t以下となる確率」を表しています。換言すれば、累積分布関数は「t以下の値が出る確率」を表しています。例えば、F(1.96)=0.975というのは、t分布に従う確率変数が1.96以下となる確率が0.975（97.5%）であることを意味します。

これは、t分布のグラフ上で、-∞ からtまでの面積に相当します。確率密度関数のグラフを考えると、横軸がt値、縦軸が確率密度を表しています。ある値tまでの累積確率を求めるということは、-∞からtまでのグラフの下の面積を計算することになります。

この面積は、その値以下の確率を直接的に表現しているため、確率の計算や比較に有用です。例えば、ある特定の範囲のt値が観測される確率を計算することができます。t値が-1.96から1.96の間に入る確率を知りたい場合、F(1.96)-F(-1.96)を計算します。

なお、t分布の累積分布関数の実際の計算は非常に複雑です。これは、t分布の確率密度関数が複雑な形をしているためです。具体的には、t分布の確率密度関数に含まれるガンマ関数や、指数部分の複雑さが、解析的な積分を困難にしています[5]。

そのため、コンピュータを使って段階的に計算を行い、近似値を求めます[6]。積分を多数の小さな区間に分割し、各区間での面積を計算して合計することで、全体の積分値を近似します。次の手順を踏むイメージです。

• 積分区間を有限の範囲に制限する
• この範囲を多数の小さな区間に分割する
• 各小区間での確率密度関数の値を計算する
• 各小区間の面積（区間の幅×確率密度）を計算する
• すべての小区間の面積を合計する

区間を細かく分割すればするほど精度が上がりますが、同時に計算量も増加します。より正確な結果を得るためには、より多くの計算ステップが必要になり、計算時間が長くなります。そのため、必要な精度と計算時間のバランスを取りながら計算を行います。

p値を求める過程で、累積分布関数は重要な役割を果たします。p値は、観測されたデータ（今回の場合はt値）が、帰無仮説のもとでどれくらい起こりにくいかを示します。累積分布関数を使うことで、この「起こりにくさ」を定量的に評価することができます。

「起こりにくさ」を定量的に評価するとは、観測されたデータがどれくらい極端であるかを数値で表現することです。ここでの「極端」とは、帰無仮説が真であると仮定したときに、観測されたデータがどれくらい珍しいものであるかを指します。

観測されたt値よりも極端な値が得られる確率を計算するために累積分布関数を使用します。「極端な値」とは、観測されたt値よりも絶対値が大きい値のことを指します。観測されたt値から、正負両方向により遠い値すべてを含みます。

例えば、観測されたt値が2.0だった場合、t≦-2.0またはt≧2.0となる確率を計算します。これは、帰無仮説（差がないという仮説）が真であるにもかかわらず、観測されたような（あるいはそれ以上に極端な）結果が得られる確率を意味します。

この確率が小さいほど、観測されたデータは帰無仮説のもとでは起こりにくいと判断できます。観測されたデータが帰無仮説と矛盾する程度が大きいと考えられるのです。この辺りはp値の計算で詳細に解説します。

p値の計算

p値を計算していきましょう。p値は、「観測されたt値以上の極端な値が、帰無仮説（2つのグループに差がないという仮定）の下で得られる確率」を表します。

これは、帰無仮説が真であるにもかかわらず、観測されたような（あるいはそれ以上に極端な）結果が得られる確率のことです。例えば、2つのグループの平均値に差がないという帰無仮説を立てたとします。しかし、実際のデータからは大きな差が観測されました。p値は、「もし本当に差がないのなら、このような（あるいはこれ以上の）大きな差が観測される確率はどれくらいか」を示しています。この確率が非常に小さければ、「差がない」という帰無仮説は支持しがたく、「差がある」と考える方が妥当だという判断につながります。

p値の計算手順を見ていきましょう。

まず、t値の絶対値を取ります。t値の正負は方向性を示すだけで、極端さを判断する際には関係ありません。そのため、絶対値を使用します。t値の符号は、どちらのグループの平均が大きいかを示すものです。p値を計算する際には、「差の大きさ」だけが問題となり、「どちらが大きいか」は考慮しません。これは、帰無仮説（差がないという仮説）を検証する際に、差の方向ではなく、差の存在自体に注目するためです。

次に、t分布の累積分布関数を用いて、|t|以上の値が出る確率を計算します。既述の通り、累積分布関数は、ある値以下となる確率を与えます。したがって、1から累積分布関数の値を引くことで、その値以上となる確率を得ることができます。

具体的には、1-F(|t|)を計算します。ここでF(|t|)は、t分布の累積分布関数で|t|以下となる確率を表します。したがって、1-F(|t|)は|t|より大きい値が出る確率を表します。これは、観測されたt値よりも極端な値（絶対値が大きい値）が出る確率を計算していることになります。

最後に、両側検定を行うため、計算した確率を2倍します。これは、正と負の両方向の極端な値を考慮するためです。t分布は対称分布であるため、正の方向に極端な値が出る確率と、負の方向に極端な値が出る確率は等しくなります。両方向を考慮するために確率を2倍するということです。

例えば、観測されたt値が2.0の場合、t≦-2.0またはt≧2.0となる確率を計算しています。t分布の対称性により、これらの確率は等しいので、t≧2.0となる確率を計算し、その2倍を取ることで両方向の確率を得ることができます。

例を用いた算出

それでは、冒頭に示した例（t=2.186, 自由度=218）を使って、p値を計算してみましょう。

t値の絶対値：|t|=|2.186|=2.186

これは単純にt値の符号をとったものです。

累積分布関数の計算：F(2.186)≈0.9850

この値は解析的に解けないため、今回はExcelのT.DIST関数を用いて計算しています。「T.DIST(2.186, 218, TRUE)」という関数で算出しました。2.186はt値、218は自由度、TRUEは累積分布関数を使用することを指定しています。

この0.9850という値は、t分布（自由度218）において、2.186以下となる確率を表しています。–∞から2.186の間に値が収まる確率で、これは全体の約98.50%の確率を表しています。観測されたt値（2.186）よりも絶対値が小さい値が出る確率が98.50%ということです。

p値の計算（両側検定）：p値=2*(1-F(|t|))=2*(1-0.9850)=2*0.0150≈0.0300

「1-0.9850=0.0150」というのは、観測されたt値（2.186）よりも大きい値が出る確率を表しています。「2*0.0150=0.0300」は、観測されたt値よりも絶対値が大きい値（2.186よりも大きいか、-2.186よりも小さい値）が出る確率を表しています。

以上により、p値は約0.0300（3.00%）となります。

帰無仮説（営業部と開発部のエンゲージメントスコアに差がない）が真であると仮定したとき、観測されたような（あるいはそれ以上に極端な）差が生じる確率は約3.00%です。もし本当に両部門のスコアに差がないとしても、このような（あるいはこれ以上に極端な）結果が得られる確率は3.00%程度だということです。

これは、帰無仮説が真であるという前提のもとでの条件付き確率です。要するに、「差がない」という仮説を立てたときに、このような（あるいはこれ以上に極端な）データが観測される確率が3.00%だということを意味しています。この確率は非常に低いため、帰無仮説（差がない）を棄却することができると考えます。

一般的に、p値が0.05（5%）未満の場合、その結果は「統計的に有意」であると判断されます。これは、帰無仮説が真である場合に観測されたような（あるいはそれ以上に極端な）結果が得られる確率が5%未満であることを意味します。

帰無仮説が真であるという前提のもとで、このような極端な結果が生じる確率が非常に低いため、帰無仮説（差がないという仮説）を棄却し、代わりに対立仮説（差があるという仮説）を採択するのが妥当であると判断するということです。

今回のp値は0.0300で、0.05未満です。したがって、営業部と開発部のエンゲージメントスコアの差は、統計的に有意であると言えます。観測されたデータは、帰無仮説（差がない）と一定程度矛盾していると解釈できます。

ただし、この結果をもって、「この差が単なる偶然である可能性は3.00%しかない」という解釈は正確ではありません。p値は、帰無仮説が真であると仮定したときに、観測されたような（あるいはそれ以上に極端な）結果が得られる確率のことです。これは、帰無仮説が真である確率や、観測された差が偶然である確率を直接表すものではありません。

p値は、帰無仮説が真であるという条件付きの確率であり、帰無仮説が偽である確率（差が本当に存在する確率）を直接示すものではありません。条件付き確率とは、ある事象Aが起こったという条件のもとで、別の事象Bが起こる確率のことです。p値の場合、「帰無仮説が真である」という条件のもとで、「観測されたデータ（あるいはそれ以上に極端なデータ）が得られる」確率を表しています。

これは、統計的推論における重要な注意点です。p値が小さいからといって、必ずしも効果の大きさや実践的な重要性を示すわけではありません。p値は、観測されたデータと帰無仮説との矛盾の程度を示す指標であり、その解釈には慎重さが求められます。

脚注

[1] 本コラムの内容はt検定の概要を理解していることを前提に記述しています。t検定に関する解説としては、当社コラムをご参照ください。

[2] 近年では、2群それぞれの成果指標の分散も考慮した自由度を用いるWelchのt検定が用いられ、その場合の自由度の式は２群の分散を含めてより複雑になります。

[3] 確率密度関数は、連続確率変数の確率分布を表現するものですが、確率密度関数の特定の点における値を確率密度と呼びます。t分布のy軸の値は確率密度を指しています。すなわち、ここで示すグラフにおける曲線が確率密度の値となります。

[4] 「確率を足し合わせる」とは、ある値以下となるすべての可能性を合計するということです。例えば、サイコロを振って4以下の目が出る確率を考える場合、1が出る確率、2が出る確率、3が出る確率、4が出る確率をすべて足し合わせます。連続的な確率分布の場合、この「足し合わせ」は積分によって行われます。

[5] 例えば、ガンマ関数は、それ自体が積分で定義される特殊関数であり、基本的な演算の有限回の組み合わせで表現できる形での計算が一般に困難です。t分布の確率密度関数の指数部分(1+t²/ν)^(-(ν+1)/2)も、直接積分することが難しい形をしています。この部分は、tの値に応じて複雑に変化し、標準的な積分技法では解けません。

[6] 近似値にとどまるのは、連続的な曲線の下の面積を完全に正確に求めることが不可能だからです。ここにおける連続的な曲線とは、t分布の確率密度関数のグラフを指します。これを求めるには、無限に小さな区間の積分を無限に多く足し合わせる必要があります。理論上は可能ですが、実際の計算では有限の操作しか行えないため、必然的に近似となります。

---

執筆者

伊達 洋駆　株式会社ビジネスリサーチラボ 代表取締役
神戸大学大学院経営学研究科 博士前期課程修了。修士（経営学）。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、組織サーベイや人事データ分析のサービスを提供している。著書に『60分でわかる！心理的安全性 超入門』（技術評論社）や『現場でよくある課題への処方箋 人と組織の行動科学』（すばる舎）、『越境学習入門 組織を強くする「冒険人材」の育て方』（共著；日本能率協会マネジメントセンター）などがある。2022年に「日本の人事部 HRアワード2022」書籍部門 最優秀賞を受賞。東京大学大学院情報学環 特任研究員を兼務。