2023年11月2日
構造方程式モデリングとは何か 指標の全体像を描くプロセスモデルを解析する(セミナーレポート)
ビジネスリサーチラボは、2023年10月にセミナー「構造方程式モデリングとは何か 指標の全体像を描くプロセスモデルを解析する」を開催しました。
「上司が部下のエンゲージメントを高めるのは、どのようなメカニズムによるものか」
「上司が部下のエンゲージメントを高めるプロセス全体を、データ分析で検証したい」
こうした実務的な疑問に答える方法として「構造方程式モデリング」があります。構造方程式モデリングを用いることで、様々な指標の関係性を、一枚のアウトプット「パス図」に集約することができます。
本セミナーでは、当社の代表取締役・伊達 洋駆と、フェロー・能渡 真澄が登壇し、構造方程式モデリングの概要を解説しました。まず能渡より、分析手法としての構造方程式モデリングの内容を解説し、伊達より、この分析を用いることの実践的な意義や注意点を紹介しました。
※レポートはセミナーの内容を基に編集・再構成したものです。
構造方程式モデリングとは
伊達:
本セミナーでは、構造方程式モデリングとは何か、それを使うことの実践的な利点は何かを解説します。構造方程式モデリング(Structure Equation Modeling)はSEMと略されるので、本日もSEMと呼びます。
当社はクライアントワークでSEMを用いており、クライアントからの満足度も高く、実践的な手法とも言えます。まず能渡さんから、SEMの考え方について解説をしてもらいます。
能渡:
それでは、構造方程式モデリング(SEM)で示されることの概要を解説いたします。まず、構造方程式モデリングとは何かをお伝えします。
SEMは、複数の指標間の関係プロセスを解析する手法です。具体的には、分析者が仮定したモデルにおける指標間の関連を検証します。この手法は、相関分析、回帰分析、因子分析など、様々な分析手法の要素を取り入れた応用的なデータ解析です。
SEMは特に、「全体的なプロセスの検証」を行う際に利用されます。例として、従業員のエンゲージメントを向上させることを目標にサーベイを設計した場面を考えてみましょう。
この例では、エンゲージメントの向上に、「業務理解」と「働きやすさ」が重要な要因であると考えたとします。さらに、「業務理解」を向上させるための要因として「上司の助言」と業務サポートが挙げられ、「働きやすさ」の向上には「上司の業務サポート」が有効であると仮定したとしましょう。
この議論のポイントは、エンゲージメントを高める全体的なプロセスに着目している点です。エンゲージメント向上に向けて、エンゲージメントを高める要因として仕事や職場に対する認識を取り上げていますが、さらにそれを高める要因として上司の要因を考えており、影響プロセス全体を仮定しています。
このような関連プロセス全体を検証する際に用いるのが、SEMになります。
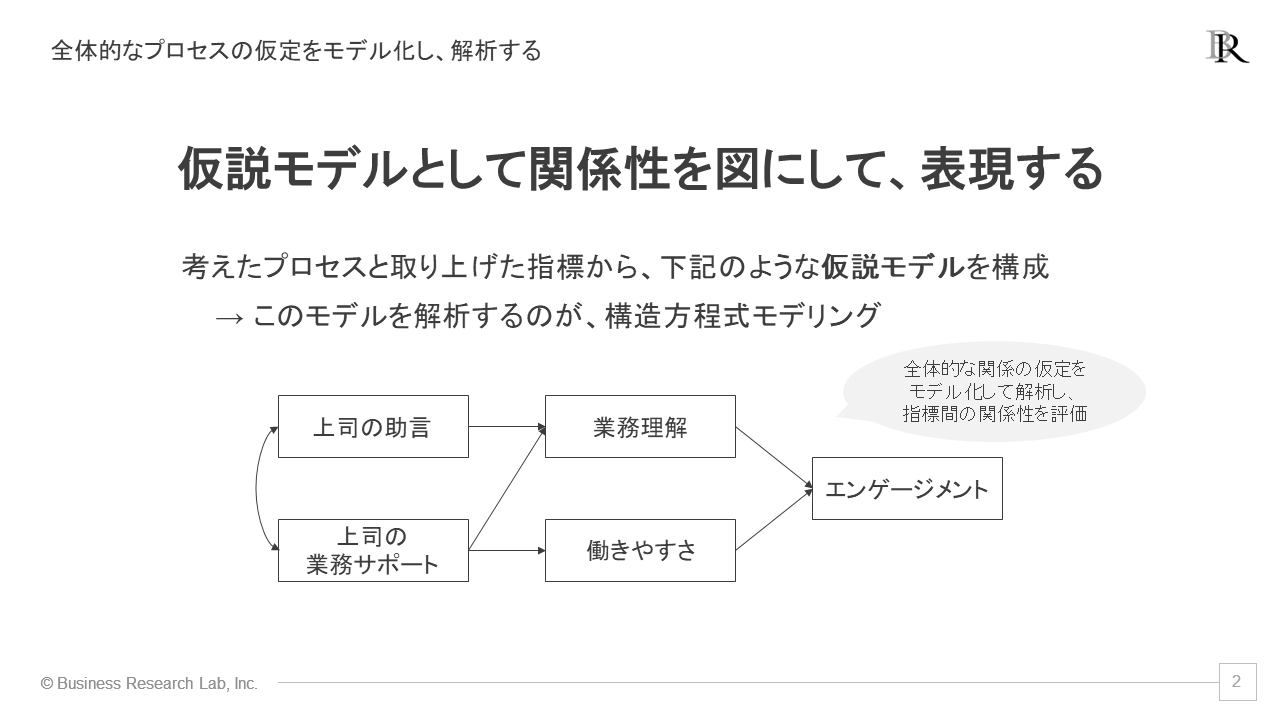
全体的なプロセスをモデル化して解析を進める際には、「仮説モデル」としてその関係性を図で表現します。例えば、先ほど述べた影響プロセスの仮定を、仮説モデルとして次の図で具体的に示します。なお、指標間の関係性を描いた次のような図のことをパス図と呼びます。
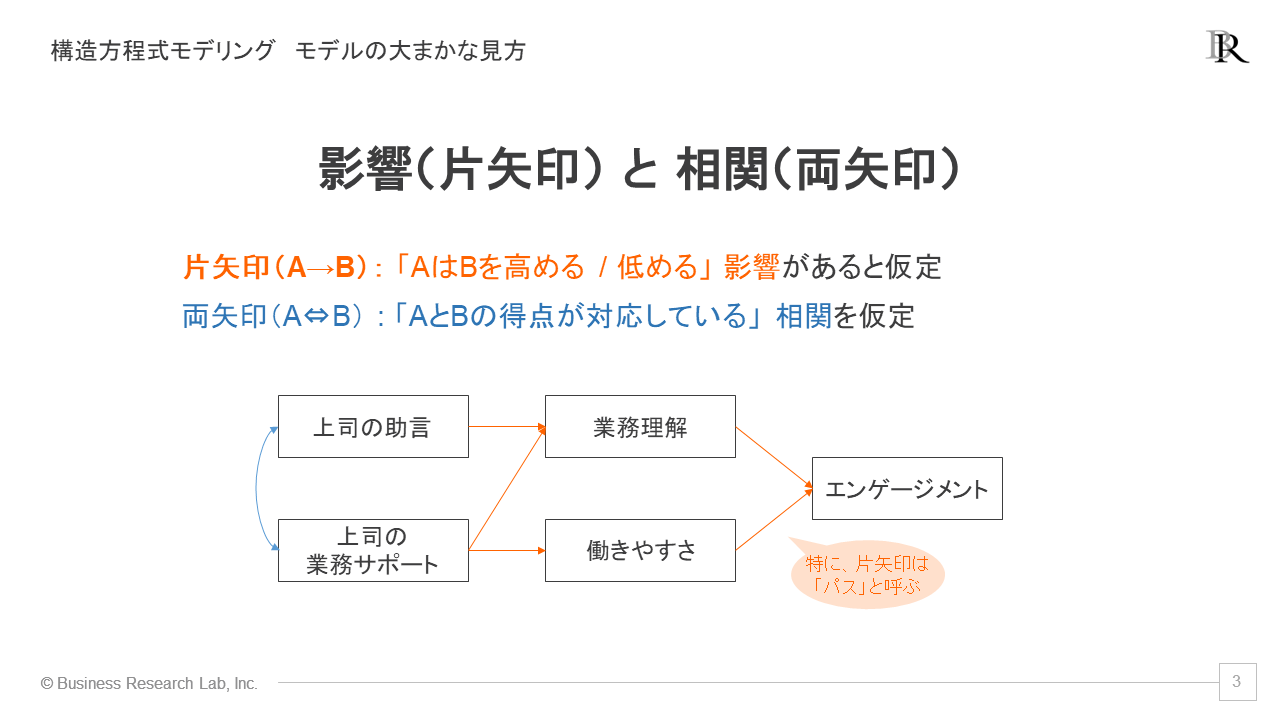
ここで、パス図の見方について説明していきます。ある指標Aから次の指標Bへ伸びる片矢印(A→B)は、AがBを高める、あるいは低めるといった影響を表します[1]。そして、二つの指標AとBを繋ぐ両矢印は、AとBの得点が対応している相関関係を表します。特に、影響を仮定する片矢印は「パス」と呼ばれます。
SEMで分かること
能渡:
SEMを用いると、主に三つのことがわかります。それは「モデルがデータに合っているか」「指標間の影響や相関について、関連性はどのくらいあるのか」「モデルの改良点はどこか」です。
一つ目に、「モデルがデータに合っているか」について、これは「モデル適合度」と呼ばれる数値で示されます。パス図で描いた影響プロセスのモデルが、実際に測定したデータにどれのくらいフィットしているかを示す情報です。
モデル適合度が良好な値を示していれば、解析したモデルはデータと合っていると判断されます。データが現実の状態を表していると考えると、仮説モデルで仮定した影響プロセスは、現実の状態をうまく捉えていると評価できるわけです。
モデル適合度に関しては、様々な指標が提案されています。その中でも、「CFI」と「RMSEA」という二つの指標を確認することが多いです。
具体的には、CFIは.90以上、RMSEAは.10以下の値であればひとまず良いとされています。これらの基準を参考にして、モデルがデータに適合しているかどうかを評価します。
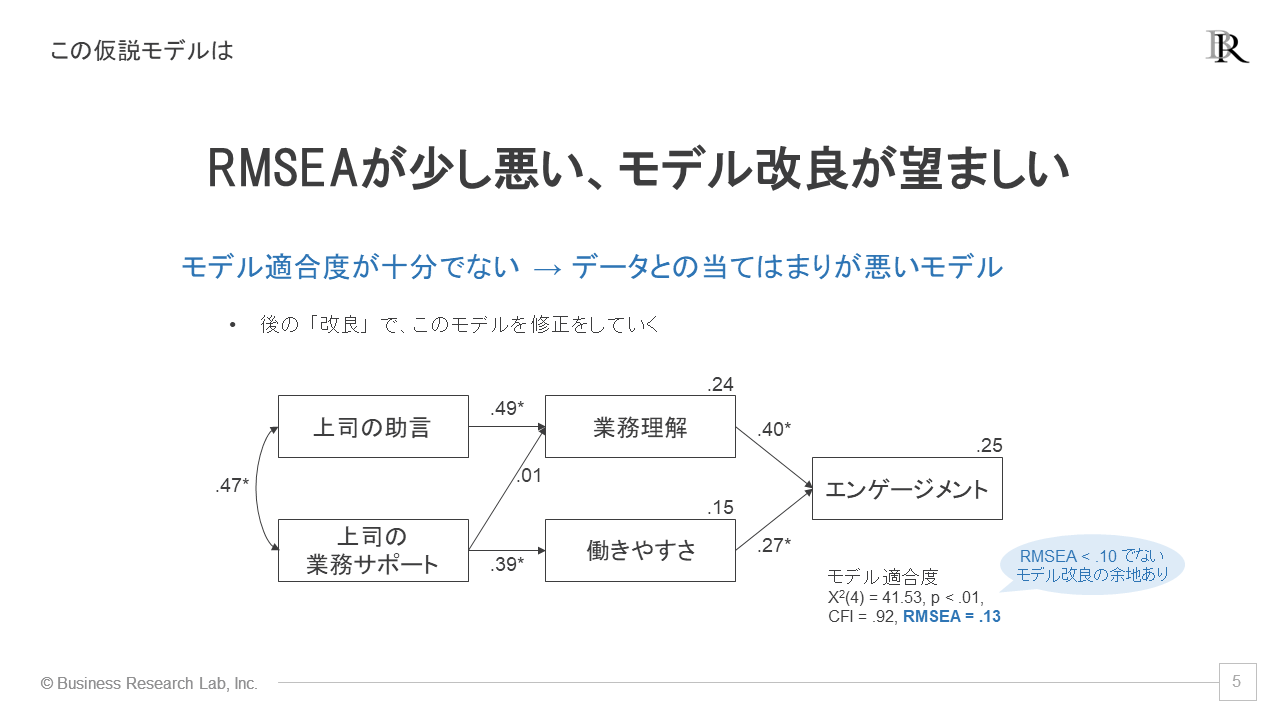
以下にダミーデータを基にした仮説モデルの解析結果を示します。モデル適合度を見ると、CFIは.90以上の基準に対して.92となっており、良好といえます。しかし、RMSEAについては.10以下の基準に対して、.13という結果です。
したがって、このモデルはRMSEAの値が基準を満たしておらず、「実際のデータに対して、仮説モデルはやや合っていない」と評価できます。このような場合、後のモデル改良で修正を加えていくことになります。
このように、データをもとに仮説モデルを評価できることは、SEMの大きな魅力の一つです。
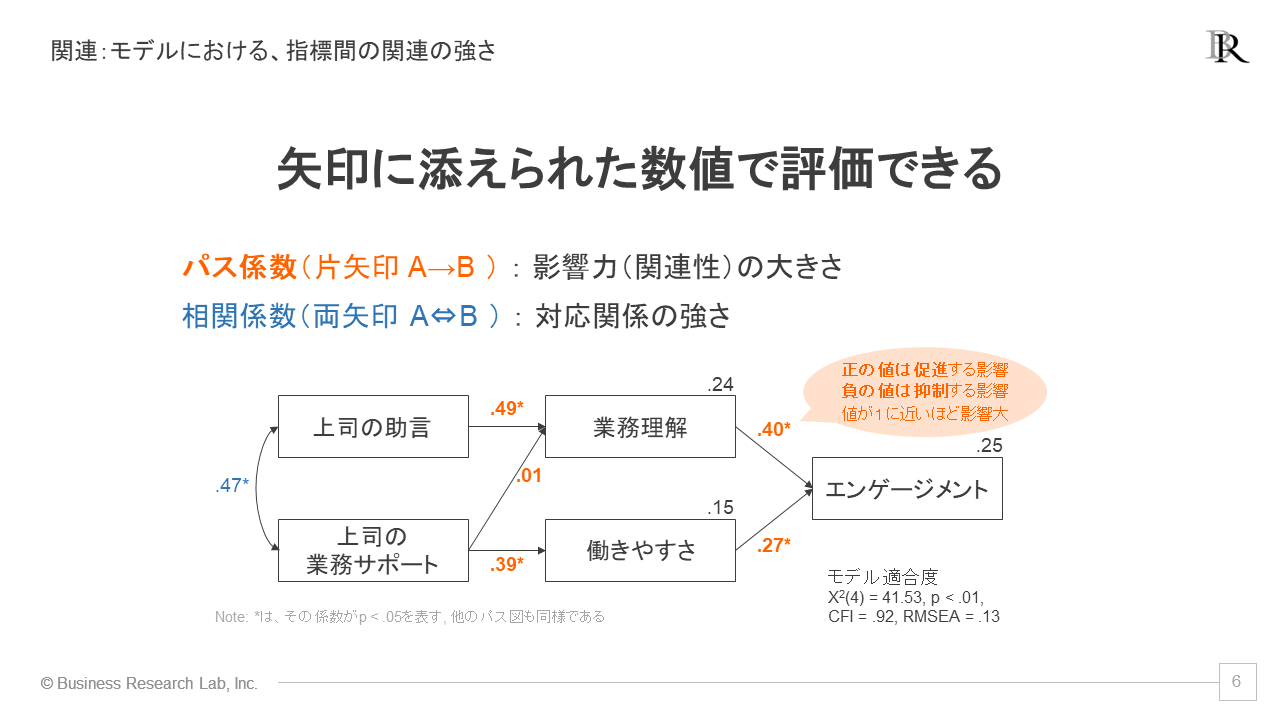
SEMで分かることの二つ目は、「指標間の影響や相関について、関連性はどのくらいあるのか」です。矢印に添えられた数値を見ることで、指標間の関連の強さを評価できます。
パスに付いている数字は「パス係数」と呼び、影響力や関連性の強さを表す指標です。そして、両矢印に付いているのが相関係数であり、得点の対応関係の強さを表す指標です。
パス係数は、プラスの値は「促進する影響・関連」、マイナスの値は「抑制する影響・関連」を表します。例えば、図の中の「.40」のように、「業務理解」から「エンゲージメント」につながるパス係数はプラスの値です。これはつまり、「業務理解が高いと、エンゲージメントが高い」という、促進的な影響を表しています。
対して、仮説モデル上には無いのですが、マイナスの値の例を考えてみましょう。例えば、ストレスとエンゲージメントをモデル上で取り上げて解析した結果、ストレス→エンゲージメントのパス係数がマイナスの値だったとします。これは、「ストレスが高いと、エンゲージメントが低い」という、抑制する影響を表します。
なお、相関係数も同様に、プラスの値は「一方の指標の得点が高いとき、もう一方の得点も高い」という得点の対応を表します。同様に、マイナスの値は「一方の指標の得点が高いとき、もう一方の得点は低い」という対応を表します。
そして、パス係数・相関係数はどちらも、+1~-1の値を取る性質があります。この値は影響や得点の対応など関連性の強さを表します。0は指標間に関連性がないことを表し、その絶対値が1に近づくほど、関連性が強いと判断します。
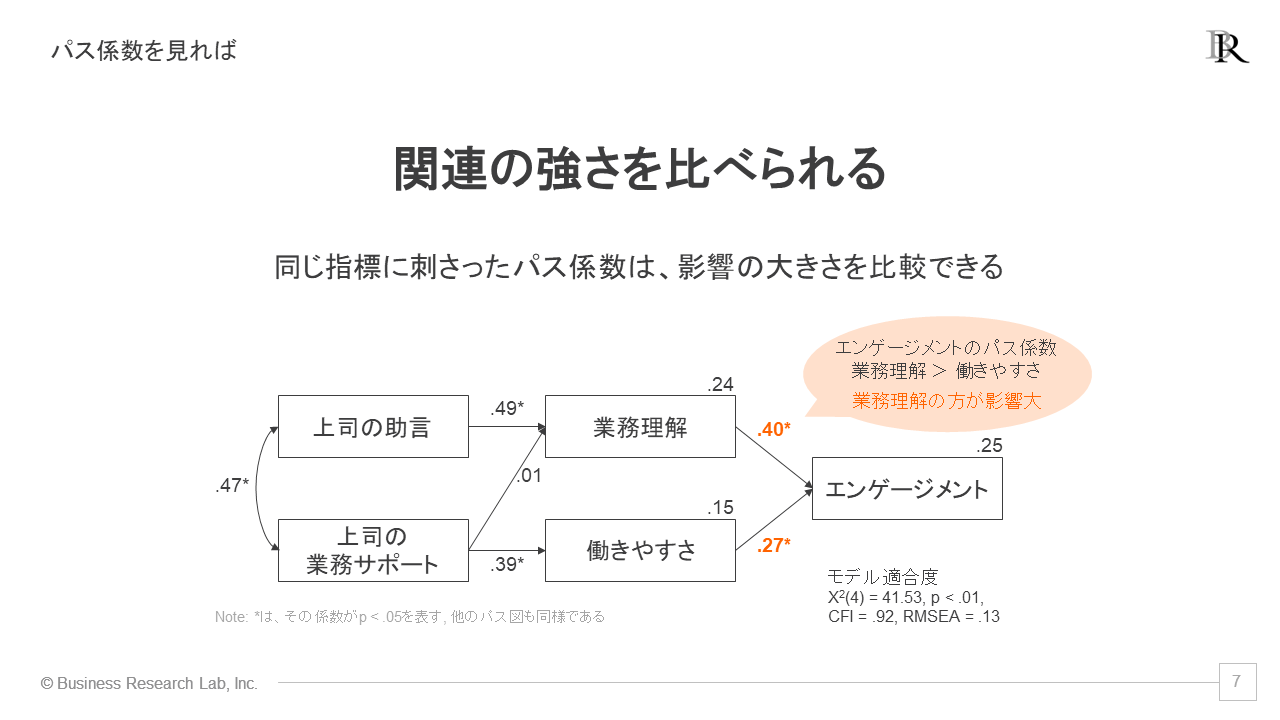
パス係数の特長として、同じ指標に刺さっているパスは、関連性の大きさをパス係数で比較することができます。例として、再びエンゲージメントに関連するパス係数を確認してみましょう。
仮説モデルでは、「エンゲージメント」に対して、「業務理解」と「働きやすさ」からパスが刺さっています。それらのパス係数を見ると、それぞれの値は.40と.27となっています。この結果から、「エンゲージメントへの影響は、業務理解の方が働きやすさよりも強い」と読み取ることができます。
このようにモデルで取り上げた指標間の関連について数値で評価できることも、SEMの魅力です。
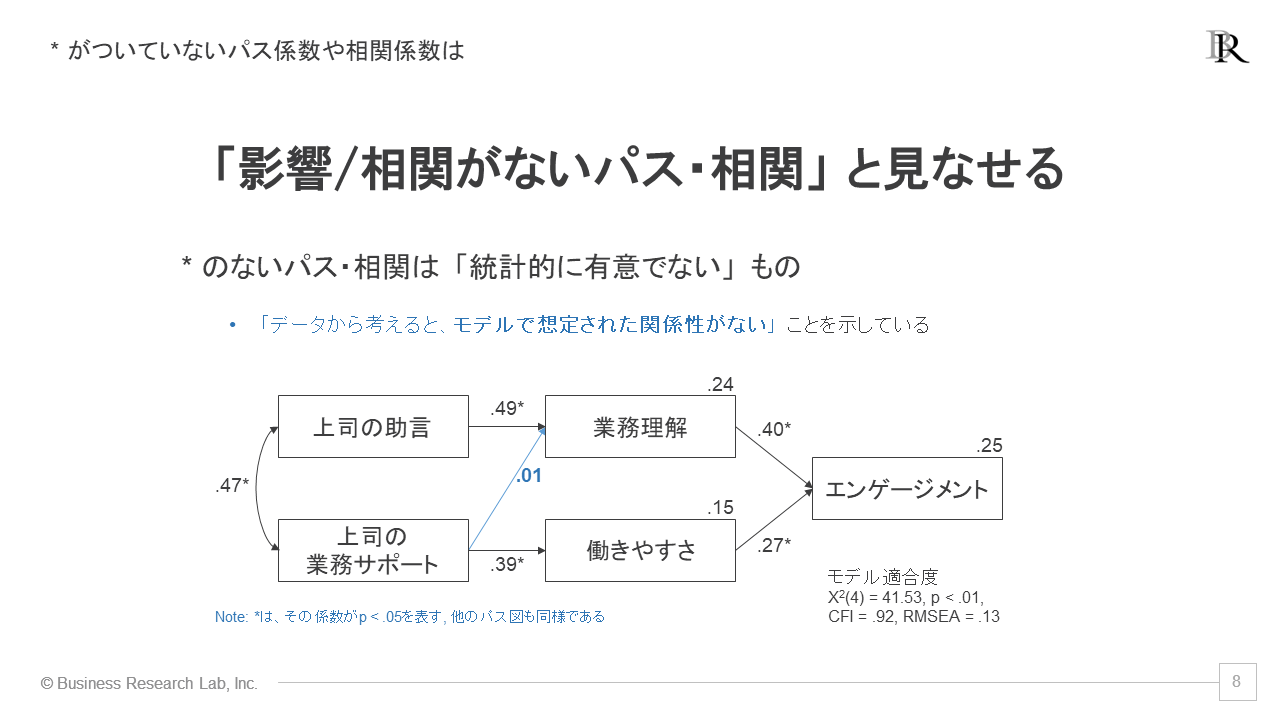
加えて、パス係数についている「*(アスタリスク)」のマークも意味があります。このマークは、パス係数や相関係数が「統計的に有意といえるか」を示したものです。本日の内容からは外れるため詳細は触れませんが、これがついていないパス係数や相関係数は、統計的に見て「影響がない、相関がない」と判断できます。
上の例では、「上司の業務サポート」が「業務理解」を高めるという仮定のもと、仮説モデルのパスを設定していましたが、解析の結果、この「*」がつかない結果でした。つまり、これらの指標間に影響関係が認められないことが、統計的に示されたということです。
このように、「統計的に有意か」を示す*の有無を見ることで、モデルにおいて影響関係が認められない部分も分かるのが、この手法のさらなる特長です。
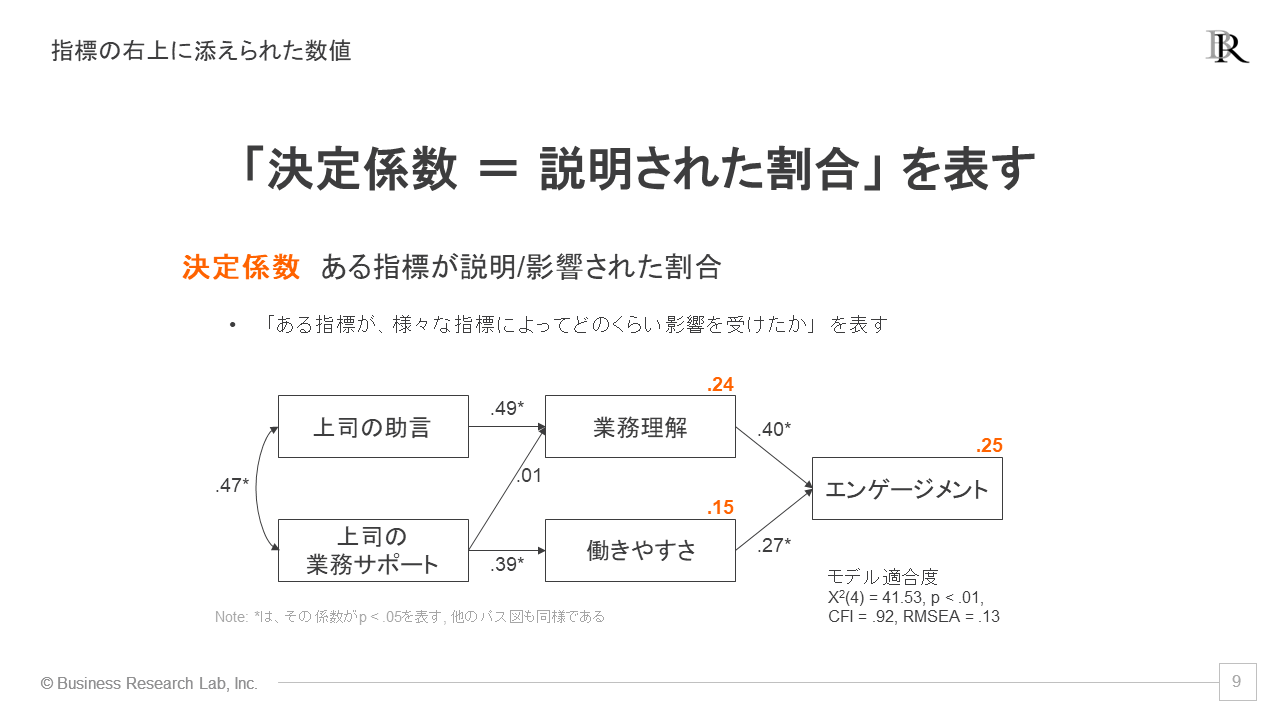
さらに、各指標の右上にも数字が付けられていますが、これは「決定係数」と呼ばれるものです。この指標は、簡単にいえば、ある指標が他の指標たちによってどのくらい影響を受けたかを合算した値です。
決定係数は、影響された指標側から見るイメージです。上記の例では、エンゲージメントに対して、「業務理解」が.40の影響を、「働きやすさ」が.27の影響を与えていましたと読み取っていました。それらの影響を合算して、エンゲージメントの得点全体はどの程度影響されたのかを見たのが決定係数のイメージです。
このように、SEMでは各指標がそれぞれどれだけの影響を与えているか、あるいは、影響された側から見て、総じてどの程度の影響を受けたといえるのかを評価することができます[2]。
SEMで得られる三つ目の情報は、「改良」に関わる指標です。データに基づいた仮説モデルの改良点が分かることが、SEMの嬉しいポイントです。
具体的には、改良点の情報は「修正指標」という数値で示されます。これは、パス図とは別枠で出力されるデータです。この指標を見ることで、より良いモデルにするためのポイントがわかります。
なお、モデルに改良すべき点があるか否かは、モデル適合度の良さで判断できます。最初にモデル適合度を確認した時点で十分な値となっていたならば、モデルの改良を考える必要はありません。すでにデータとよく合っているモデルは、さらに改良しなくてよいからです[3]。
逆に言えば、この修正指標が活きてくるのは、モデル適合度が低く、「モデルの改良が必要だ」と考えられた時です。
修正指標は、現状のモデルに対して、追加するとよいパスや相関が提示されます。この指標は、値が大きいパスや相関をパス図に追加し、その改良モデルを再度解析するという流れで使います。
上記の例では、「上司の助言→働きやすさ」の影響を示すパス追加の修正指標が大きいため、そのパスをすればよいとわかります。その部分のパスを追加し、再びモデルを解析すればよいわけです。
ダミーデータですが、先ほどの仮説モデルについて、修正指標を活用してモデル改良した結果を見てみましょう。最初のモデル適合度はRMSEA = .13であり、基準値の.10以下を満たしていませんでした。そのため、修正指標によるモデル改良が必要と判断できます。
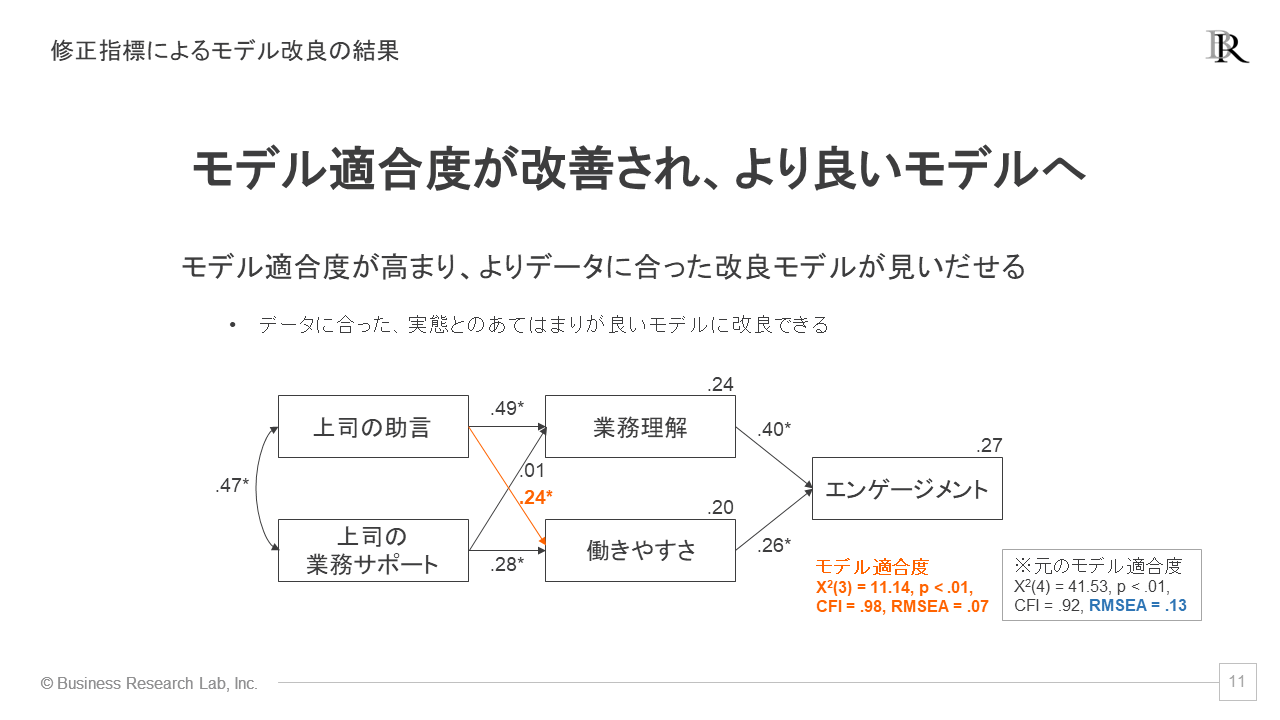
修正指標を参考に、「上司の助言→働きやすさ」へのパスを追加した改良後のモデルを作成し、再度解析した結果が次のものです。
改良後のモデルを解析した結果では、モデル適合度のRMSEAが.07と、.10より低くなり、モデルの適合度が向上しました。さらに、CFAは.92と元から良い値でしたが、それも.98へと上昇しています。モデル改良によってモデル適合度が向上したことが確認できます。
加えて、追加したパスを見てみると、「上司の助言→働きやすさ」のパス係数は、.24でアスタリスクがついています。つまり、これは有意なパスということで、2指標間の影響関係が新たに見いだされた形です。
このように修正指標を見ることで、モデル適合度が良くないモデルを改良し、想定していなかった指標間の関係性が見えてくる可能性があります。
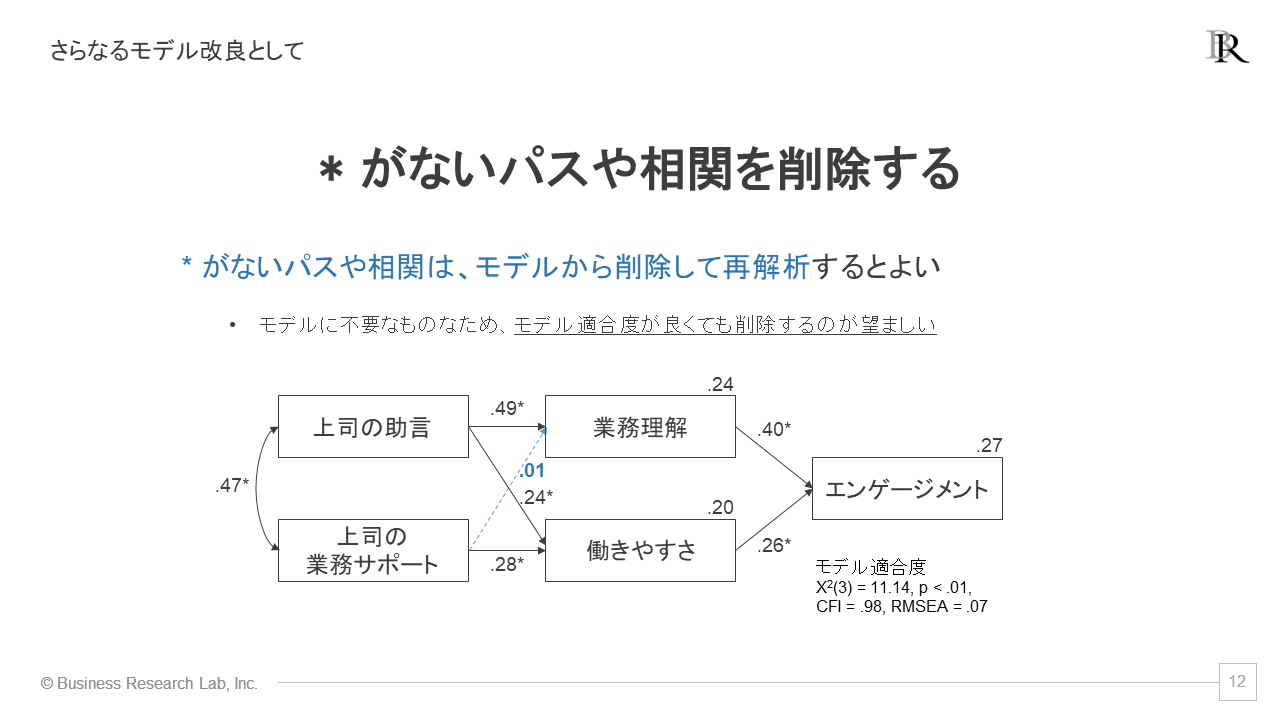
そして、さらなるモデルの改良方法として、「*」マークがついていないパスや相関を削除することが考えられます。「*」マークがついていない場合、その関連性が統計的に有意でなく、影響や相関がないことを示しています。従って、そのパスをモデルに含めておく必要がないと判断できるわけです。
なお、*がついていないパスや相関の削除は、モデルの適合度が良い場合でも実行して、再解析することが望ましいです。モデルが洗練されたものとなります。これらの改良を経て、データに基づく最終的なモデルが完成します。
更なる解析オプション
能渡:
次に、SEMの解析で使用できるオプションをご紹介いたします。このオプションを活用することで、モデルの検証をより詳細に行うことが可能となります。
SEMのオプションは多種多様ですが、本日はクライアントからのご要望が多い、属性ごとの比較を行うオプションを紹介したいと思います。具体的には、年代などで回答者をグループ分けして検証したいという場合に使える、「多母集団同時分析」と呼ばれる方法を取り上げます。
例えば、先ほどの改良後モデルについて、若手社員とベテラン社員で違い見られるか検証してみたい考えがあるかもしれません。その場合は、多母集団同時分析で対応できます。
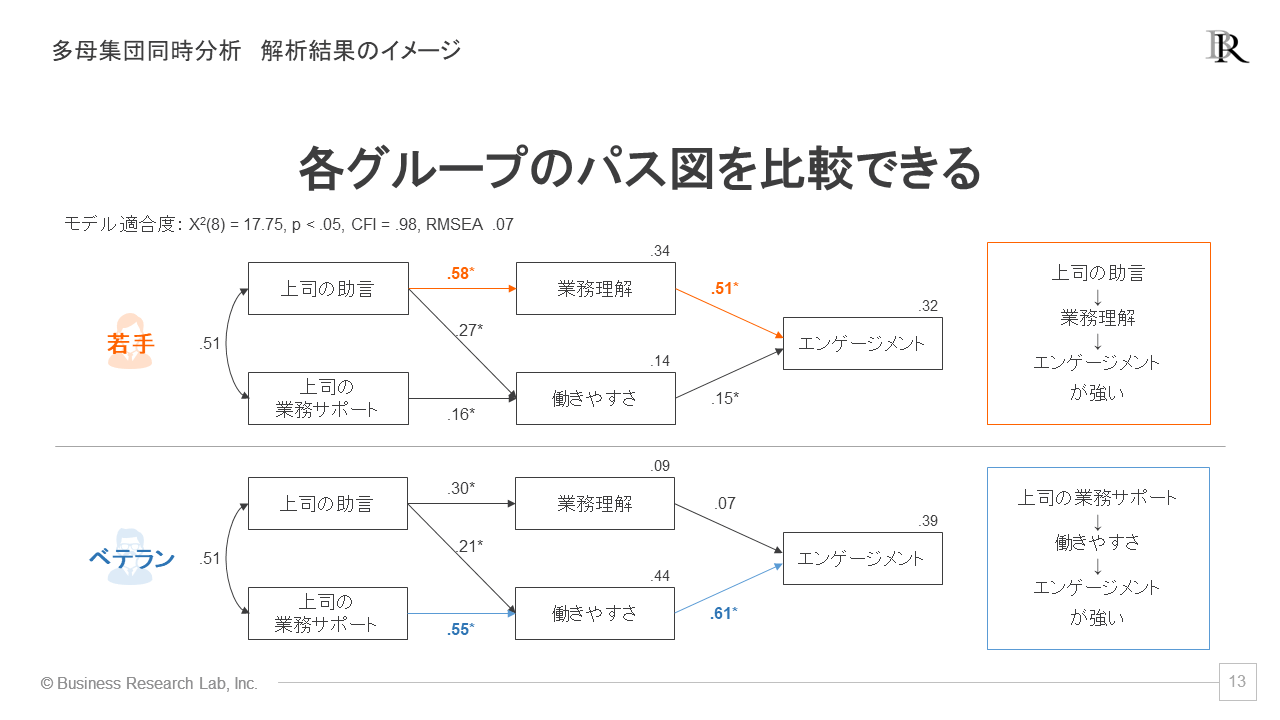
本日は概要なので詳細は割愛し、どういった解析が可能かだけお見せします。以下にダミーデータを用いた多母集団同時分析の例として、若手・ベテランで分けたグループごとの解析結果を示しております。このように多母集団同時分析では、それぞれのグループで同じパス図を解析し、その違いを検証できるのです。
上の図で、若手とベテランの違いを見てみましょう。若手のパス図では、「上司の助言→業務理解→エンゲージメント」のパス係数が大きいことが確認できます。「上司の助言→業務理解」で.58、「業務理解→エンゲージメント」で.51と、パスが伸びています。
これを踏まえると、若手においては、エンゲージメントを高めるプロセスとして、「上司の助言」が「業務理解」を向上させ、その「業務理解」がエンゲージメントを高める流れが強いと解釈できます。
一方、ベテランのパス図を見ると、「上司の業務サポート」が「働きやすさ」に影響し、「働きやすさ」が「エンゲージメント」に影響する関連性が強いことが示されています。ここから、ベテランのエンゲージメントを高めるプロセスは、「上司の業務サポート→働きやすさ→エンゲージメント」の流れが強いと考えられるわけです。
このように、多母集団同時分析を活用すれば複数のグループに分けてパス図を解析でき、それぞれのグループにおける特徴的な影響プロセスを把握することができます。
これ以外にも、SEMには様々な分析オプションがあり、使いこなせば非常に有用で興味深い解析結果を見出すことができるようになります。
SEMの実践的意義
全体を俯瞰できる
伊達:
私からは、構造方程式モデリング(SEM)の実践的意義を四つ紹介します。
一つ目は、全体を俯瞰できる点です。SEMを使用することで、様々な指標間の関係を一覧できます。これにより、全体像を理解することができます。
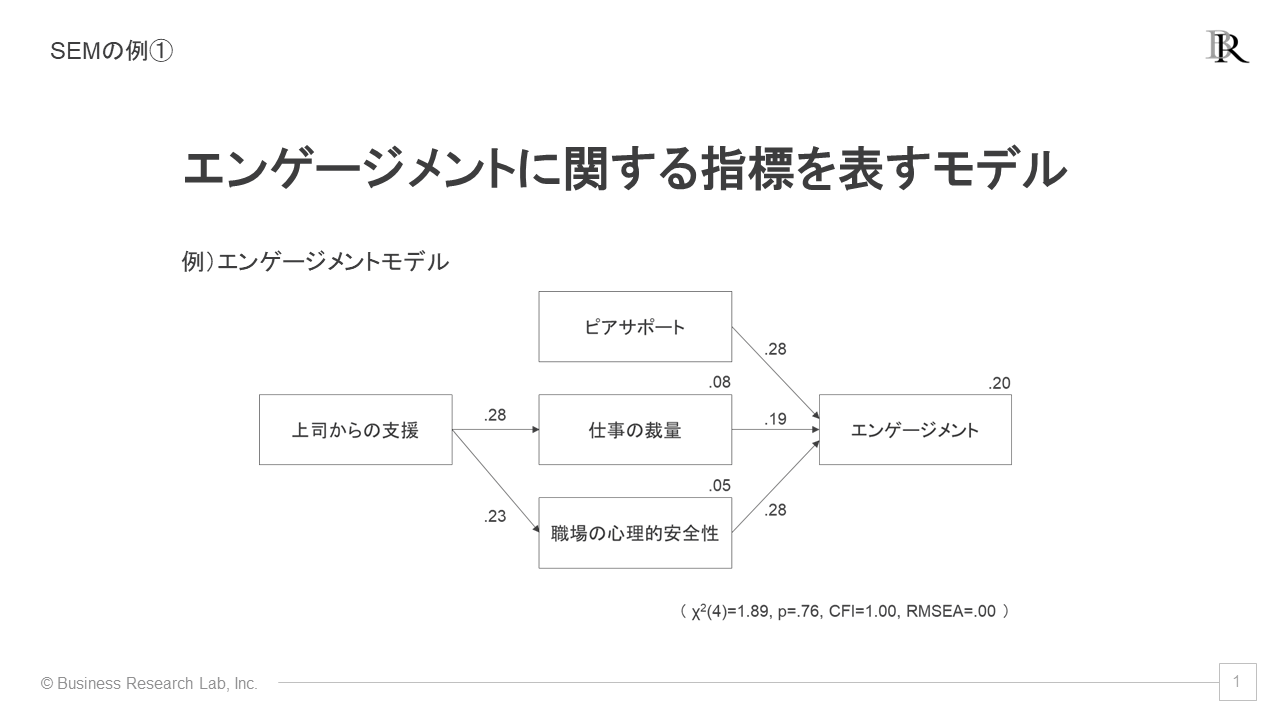
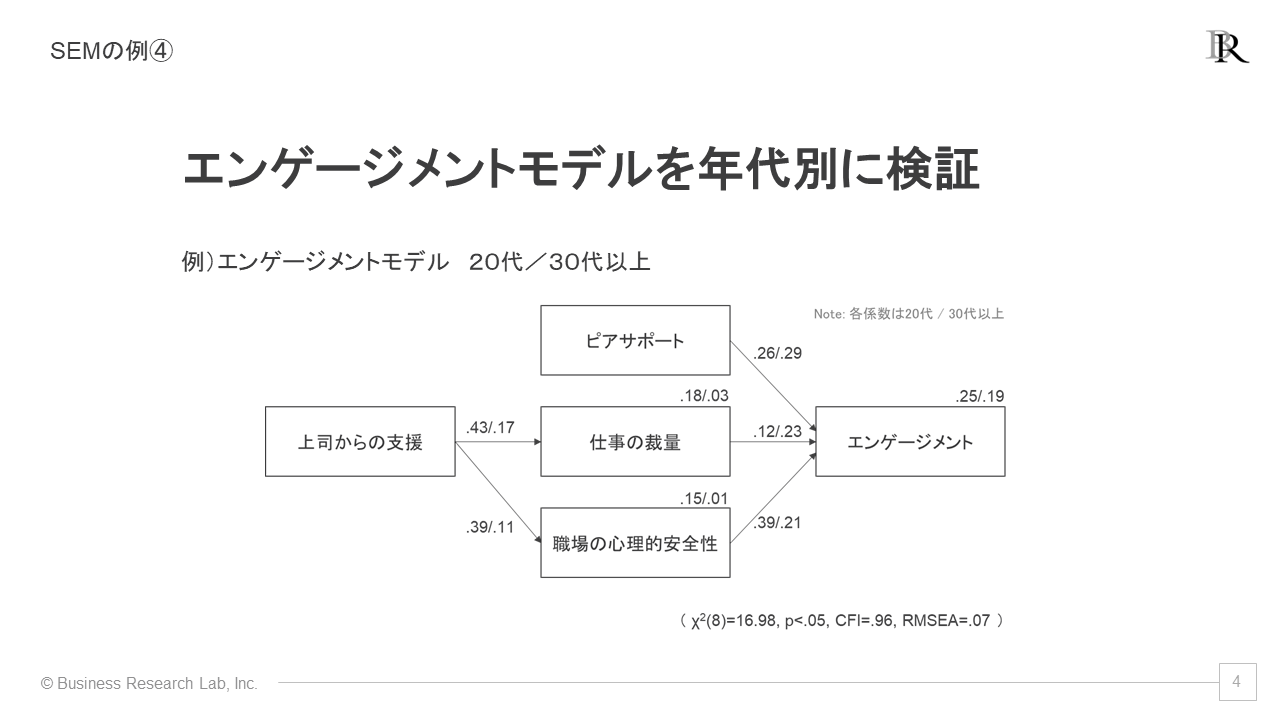
エンゲージメントに関する組織サーベイを行った例を考えてみましょう。エンゲージメントに影響を及ぼしている要因として、「ピアサポート」「仕事の裁量」「職場の心理的安全性」が挙げられます。特に「ピアサポート」と「心理的安全性」の影響が強いことが確認できます。
さらに、「仕事の裁量」や「職場の心理的安全性」に対して「上司の支援」が重要な役割を果たしています。このように、エンゲージメントに関する要因を一つのモデルで表現することで、指標間の関係を確認することが可能です。
組織サーベイや社内データの分析においては、単純集計、相関分析、回帰分析など、多岐にわたる分析を進めます。多くの結果が得られ、それぞれの結果は有益かもしれませんが、全体としての結論が不明確になることがあります。これに対して、SEMを用いれば、全体の関係を簡潔に把握することができ、便利です。
結果を一つのモデルで表現することができる点も、有益だと言えます。SEMの結果がエグゼクティブ・サマリーの役割を果たします。実際、経営層に分析結果を報告する際に、SEMの結果が使えます。「このような結果が得られました」と全体像を示せます。
要因とその要因が分かる
伊達:
二つ目の実践的意義として、人や組織が目指すべき状態である成果指標を促進する要因が分かります。さらには、成果指標の要因を促進する要因も明らかにすることができます。つまり、成果指標の要因と、要因の要因が分かるのです。
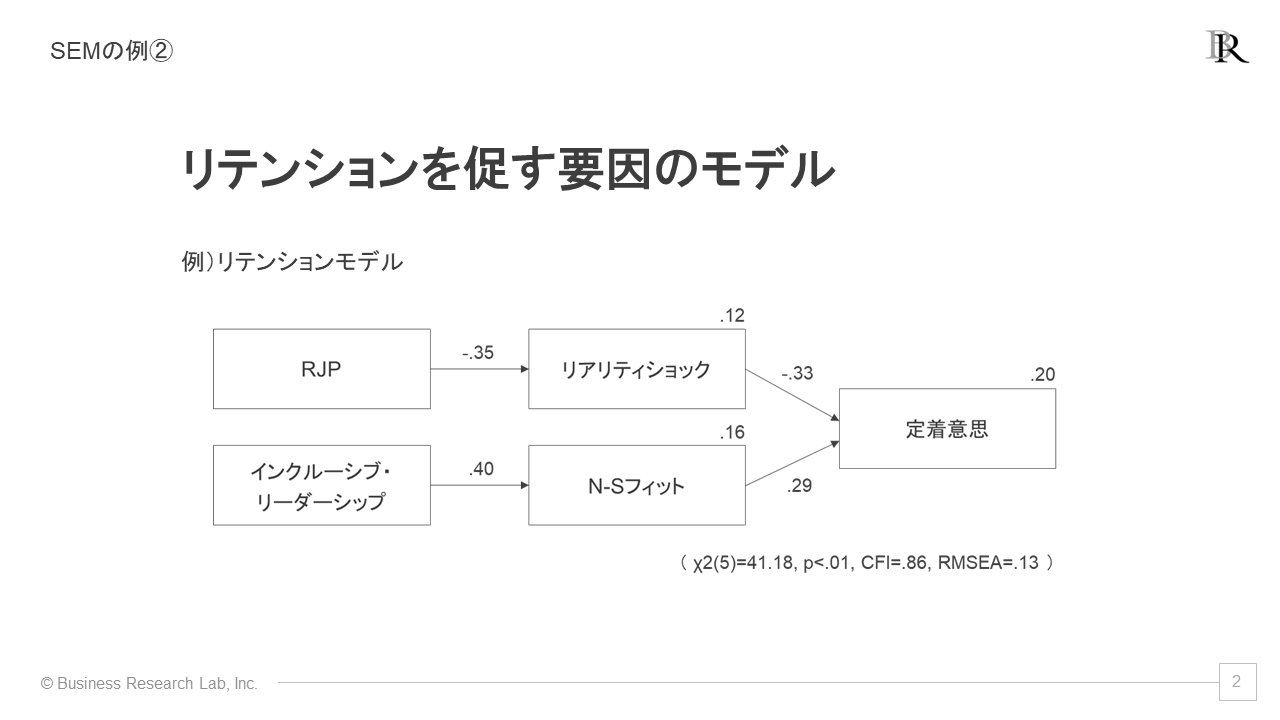
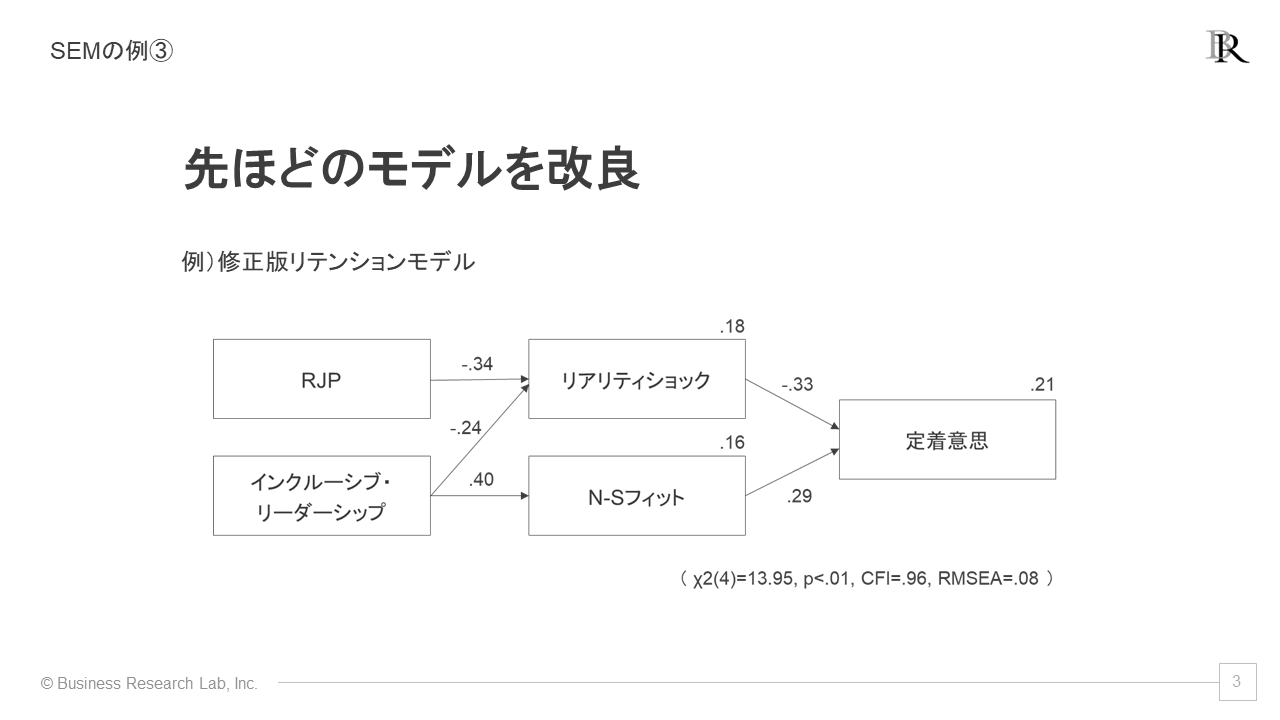
リテンションモデルを検証した仮想例を参考にしましょう。成果指標は「定着意思」で、その会社に残りたいと感じる気持ちを意味します。定着意思を高めるための要因として、「リアリティショック」と「N-Sフィット」があります。
リアリティショックは、入社前の期待と入社後の実態のギャップによる衝撃です。これが大きい人ほど定着意思が低下します。一方、「N-Sフィット」は、従業員のニーズを満たす環境が整っている度合いであり、これが高い人ほど定着意思は高いことが分かりました。
このうち、リアリティショックを軽減するためには、「RJP」と呼ばれる、実態を正確に伝える採用活動が効果的です。また、N-Sフィットを高めるためには、上司の「インクルーシブ・リーダーシップ」が重要です。これは、部下が上司に相談しやすい環境を作るリーダーの行動を指します。
このように、成果指標の要因、および、それらの要因の要因まで理解できると、多角的に人事施策を検討できます。
先ほどの例では、リアリティショックによって定着意思が下がらないよう、RJPという採用の施策が必要と判断できます。他方で、N-Sフィットを高めるためには、インクルーシブ・リーダーシップを育成することが重要とわかります。
また、モデルを構成する指標について、現在の数値を比較することで、伸びしろが見えてきます。例えば、インクルーシブ・リーダーシップは比較的高い数値を示し、RJPはまだ低い数値であったとします。RJPは他の指標に比べて伸びしろがあることが分かります。
思わぬ修正ができる
伊達:
三つ目の実践的意義として、思わぬ修正ができる点が挙げられます。SEMではモデルの改良が行えます。初めに想定したモデルでは十分な適合度が得られないこともあるでしょう。よりデータに合致するモデルを検討する中で、予想外の発見が生まれるかもしれません。
先ほどのリテンションモデルを改良した例を考えます。修正版では、インクルーシブ・リーダーシップからリアリティショックへのパスが追加されています。相談しやすいリーダーがいると、リアリティショックも緩和されることを示しています。
この結果を見ると、インクルーシブ・リーダーシップのさらなる重要性が明らかになります。フィット感を向上させると同時に、リアリティショックも軽減できるからです。RJPを行うより先に、リーダー育成を行うべきという判断が下せるかもしれません。
ターゲティングができる
伊達:
SEMの実践的意義の四つ目は、ターゲティングが可能になる点です。多母集団同時分析によって、特定の集団の特徴が明確化できます。
例えば、20代と30代以上の2グループでエンゲージメントモデルを検証したとします。「上司からの支援」から「仕事の裁量」と「心理的安全性」へのパスに二つの係数が記載されていますが、左側は20代の値、右側は30代以上の値です。係数を比較すると、20代の方が上司からの支援が重要であることがわかります。
全社一律の施策で等しく効果が得られることは稀有です。属性によって効果は違ってきます。どんな施策を講じると、どの属性で効果が高まりやすいのかが、SEMによって見えてきます。
SEMの注意点
モデルの自作が必要
伊達:
続いて、SEMを使用する上での注意点を紹介します。一つ目は、モデルが最初から与えられているわけではない、という点です。
これまでいくつかのモデルを紹介しましたが、SEMの分析では自動的にモデルが現れるわけではありません。分析者が、変数間の関連性を自ら考えて、モデルを構築する必要があります。
理論やエビデンスを参考に、質の高いモデルを自作しなければなりません。このプロセスは簡単ではありませんが、良質なモデルを構築すれば意義深い分析ができます。
サンプルサイズの問題
伊達:
二つ目の注意点は、サンプルサイズです。分析に用いるデータが少ないと、SEMの推定がうまくいきません。ある程度のサンプルサイズが必要になります。手元に数十名のデータがあっても、すぐに活かせるわけではありません。
因果関係は保証していない
伊達:
三つ目の注意点は、因果関係を保証するわけではないことです。SEMのモデルの中で、パスは矢印で示されています。しかし、それは必ずしも因果関係を意味しません。SEMの結果だけをもとに、因果関係があると述べるのは早計です。
Q&A
Q: 決定係数の基準はあるか
能渡:
はい、決定係数は効果量という指標の一つで、基準値として参照される値が存在します。効果量の基準では、決定係数はR2 = .13を超えていれば、中程度の効果量として十分に説明されていると判断されます。
Q: SEMと比べたときの従来の分析のメリットはあるのか
能渡:
SEMはとても万能な解析手法ですが、難点が二つあります。まず、モデルの自作やモデル改良に際して、正確に行うには多くの知識とデータ解析技術が必要です。加えて、他の分析手法以上にサンプルサイズが求められます。少なくとも100人以上、あるいはモデルに含めた指標の個数の20倍以上の人数が必要とされています。
一方、相関分析や回帰分析など他の分析手法は、それほど大きなサンプルサイズを必要としない点や、熟練したスキルはそれほど求められないため、いくらか気軽に使えるメリットはあると言えるでしょう。
Q: SEMで示される「効果」と「因果関係」にはどんな違いがあるか
能渡:
「因果関係」とは、ある指標が変わることで、続く指標も確実に変わるという明確な関係を指します。一方、SEMで示される「効果」は回帰分析を基盤としており、厳密にいえば、あくまで指標のデータ間に関連があることを示すものです。
測定したデータにおいて関連が見られることは、必ずしも因果関係を意味しません。因果関係を断定する際は、他の要因も十分に考慮する必要があり、SEMの分析結果のみで因果関係を主張するのは早計といえます。
伊達:
因果関係を示すには、満たすべき条件がいくつもあります。その中には、分析だけではどうにもならない条件もあります。
Q: 仮説モデルはどのように作成すればよいか
能渡:
最後に位置づけられた指標の直前には、それを促進・抑制しそうな従業員の内面的な心理指標を配置することが多いです。例えば、仕事のやる気を表す「ワークエンゲージメント」を最終的な目標となる指標に位置づけた場合、その前には「働きやすさ」「評価の公平感」「上司関係満足」など、内面的な心理的指標を置きます。
そうして配置した内面的な指標に対して、それらを高めそうな外的要因を、さらにその前に置くのがコツです。例えば、「上司の行動」や「仕事の特徴」など、対人交流やジョブデザイン、組織制度といった外的な要因を一番左に配置すると、解釈しやすい結果が得られます。
伊達:
「なぜ、その指標間に関連があると言えるのか」を説明してみるのも良いでしょう。例えば、「上司からの支援」がなぜ「ワークエンゲージメント」に影響するのか説明できるか考えてみます。説明できない場合は、パスを想定するのに慎重になったほうが良いと思います。
Q: SEMを行う上でどんなツールがあるか
伊達:
例えば、有名なフリーソフトなら、「R」と呼ばれる統計ツールや、Excelのマクロを利用した「HAD」でSEMの解析ができます。有料ツールなら、「Amos」や「Mplus」が有名です。
Q: 多母集団同時分析でモデルごとに適合度は変わるのか
能渡:
複数のグループに分けてそれぞれパス図を解析するのが多母集団同時分析ですが、大きな特徴として、グループがいくつあってもモデル適合度は常に1つだけ示されます。χ二乗値やCFI、RMSEAは、常に1つだけ示されるということです。
Q: 仮説モデルを変更するためにはアンケート項目の修正も必要か
能渡:
SEMでモデルを解析・改良する展開の中では、仮説モデルの変更に際してアンケート項目の修正は必要ありません。解析時におけるSEMのモデル構築・改良は、あくまで測定したデータ内で指標間のパスや相関を仮定・追加・削除していくため、項目の修正は考えません。
脚注
[1] ここでは分かりやすさを重視して「影響」と述べていますが、後述の通りSEMの分析のみでは因果関係を実証できないため、厳密には因果を強調するこの表現は適切ではありません。因果関係の実証に向けた取り組みをしていないデータにおいてSEMの解析結果を述べるとき、A→Bのパスは「関連」と述べた方がより適切といえます。
[2] パス係数・相関係数・決定係数に関する詳細は、当社のコラム「人事のためのデータ分析入門:回帰分析~要因を見出すための分析~(セミナーレポート)」・「人事のためのデータ分析講座 相関分析 ~2つの指標の関連を検証する~(セミナーレポート)」で紹介しています。
[3] むしろ、とにかく適合度を高めようとモデル改良しすぎることは不適切とされています。適合度を高めるモデル改良は「手元のデータに合うモデルに調整していく行為」であり、それをやりすぎると「手元のデータにだけ非常に合うモデル」が生まれるためです。SEMの解析では「様々なデータ・実態に当てはまる、適用範囲の広いモデル構築」が目的なため、その時得られた手元のデータにだけ合うモデル構築は目的に合っておらず、不適切といえます。
執筆者
 伊達 洋駆 株式会社ビジネスリサーチラボ 代表取締役
伊達 洋駆 株式会社ビジネスリサーチラボ 代表取締役
神戸大学大学院経営学研究科 博士前期課程修了。修士(経営学)。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、組織サーベイや人事データ分析のサービスを提供している。著書に『60分でわかる!心理的安全性 超入門』(技術評論社)や『現場でよくある課題への処方箋 人と組織の行動科学』(すばる舎)、『越境学習入門 組織を強くする「冒険人材」の育て方』(共著;日本能率協会マネジメントセンター)などがある。2022年に「日本の人事部 HRアワード2022」書籍部門 最優秀賞を受賞。
 能渡 真澄
能渡 真澄
株式会社ビジネスリサーチラボ フェロー。信州大学人文学部卒業、信州大学大学院人文科学研究科修士課程修了。修士(文学)。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を、他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており、通常では捉えることが困難な、様々なデータの背後にある特徴や関係性を分析・可視化し、その実態を把握する支援を行っている。