ビジネスリサーチラボは、2023年3月にセミナー「人事のためのデータ分析講座 〜 t検定：平均差の検証方法を学ぶ 〜」を開催しました。

「昨年と今年のエンゲージメントの平均値を比べたい」「他社と自社で、マネジメント力に違いがあるのかを検討したい」など、二つのグループの平均値の差を検証するシーン等で有効なのが「t検定」です。t検定は、組織サーベイや社内データを分析する際に活用できるだけでなく、他の統計分析を理解する基礎にもなります。

講師はビジネスリサーチラボ フェローの能渡真澄が担当し、t検定の実務における利用場面や、分析の進め方などを解説しました。

※本レポートはセミナーの内容を基に編集・再構成したものです。

１．t 検定とは何か

本日のテーマは、t検定です。これは、２つのグループ間の平均差を検証するシーンなどで有効な分析です。人事領域でも、組織サーベイや社内データを分析する際に活用できる、有効な手法となります。

はじめに、t検定とは何かについて説明します。例として、上司のリーダーシップ力を高めるための研修を企画して実施したと仮定します。

研修終了後、「その研修に効果はあったのか検証したい」ことは多いでしょう。そこでよく行われるのが、アンケートなどでリーダーシップの程度を測定し、その高さを研修前後の平均点で比べることです。

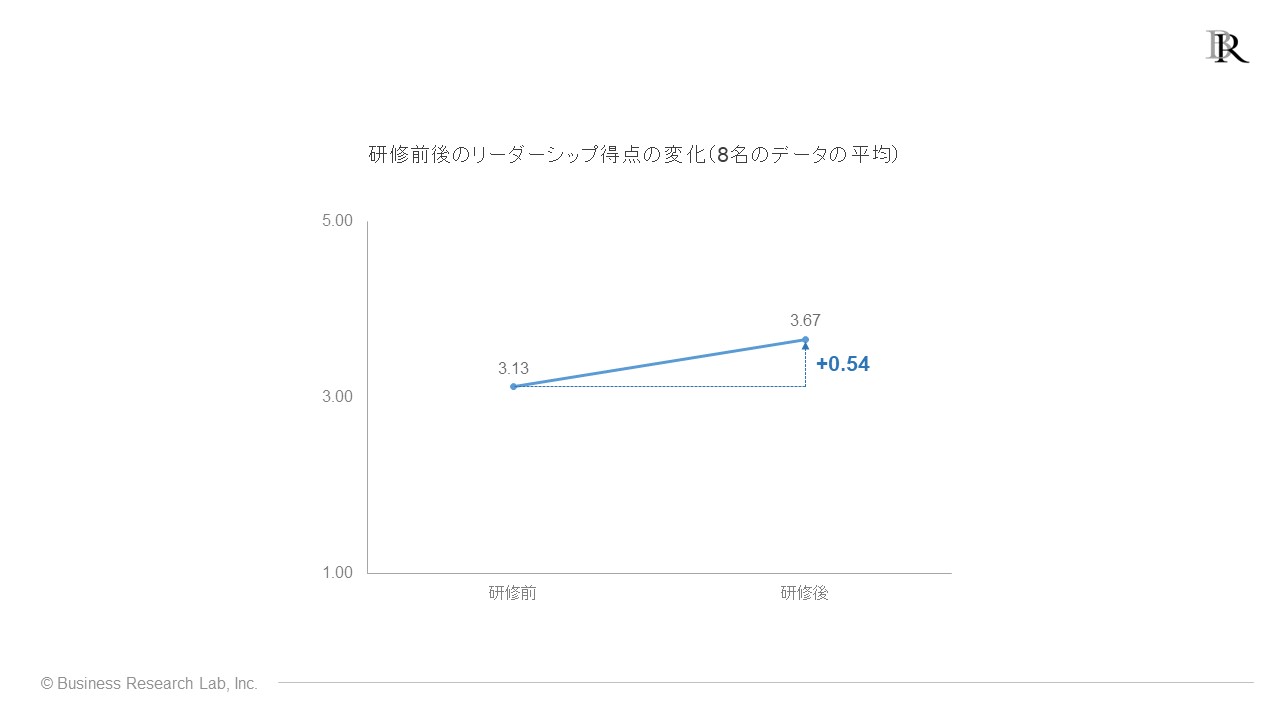
以下は、架空のサーベイ結果です。8名が受講したリーダーシップ研修において、研修前後のリーダーシップ得点が示されたグラフがあります。

ここでは、リーダーシップを測定する質問３項目を「１：まったくあてはまらない～５：とてもあてはまる」の選択肢で測定し、３項目の平均得点を各受講生のリーダーシップ得点とした状況を想定しています。

この例では、研修前は8名の平均3.13点であったリーダーシップ得点が、研修後には平均3.67点となりました。このデータから、リーダーシップ得点が0.54点上昇していることが確認できます。この結果をもとにすると、「研修はリーダーシップを高める効果」があると主張したいところです。

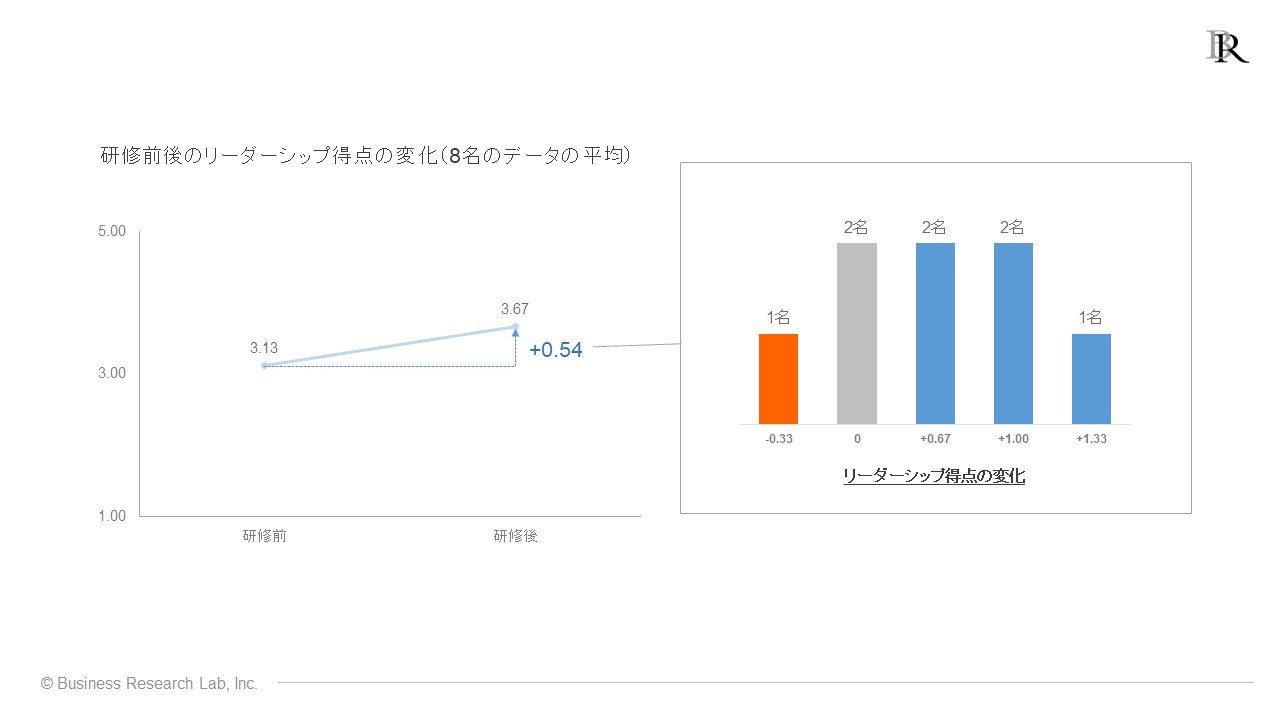
しかし、よく指摘される疑問や批判があります。具体的には、「今後の同様の研修でも、同じような成果が期待できるのか」という点です。先ほどのデータを詳しく見ると、以下のような詳細になっていたとします。

例えば、「リーダーシップ得点の変化には、受講者間で大きなばらつきがある」と考えることができます。確かに、平均的には研修前後で0.54点上がっていますが、その中身を詳しく見ると、得点が変わっていない人もいれば、得点が減少した受講者もいます。

この事実に基づいて、「今回、平均して得点が上がった結果が出たのは偶然ではないか。この研修で、今後も平均的なリーダーシップ向上は見込めるのか」と考えるかもしれません。

こうした懸念は、推測統計で検証が可能です。推測統計とは、サーベイで得られたデータから、サーベイの対象者全体の特徴を推測する分析枠組みです。

あるサーベイで示された結果がそのとき偶然得られた可能性を、完全に排除することはできません。しかし、その限定的なデータがもつ特徴をうまく活用することで、「母集団」と呼ばれる、未測定の対象者全体の状態をある程度推測することができるのです。

では、推測統計をどのように利用すれば、上述の問題を解消できるのかを説明します。まず、手元のデータには、先に述べたような受講者ごとのばらつきが存在します。平均的には0.54点上昇していましたが、上昇の程度は様々だということです。

このばらつきを考慮した上で、母集団における得点の上昇を評価する分析手法の1つの手段が、t検定です。これは、二つのグループの平均が異なるかを統計的に評価するもので、帰無仮説検定の一種です。

t検定を行うと、今回のデータで示された得点の差異が偶然生じたものか検証できます。それにより、「今回示された平均差は、偶然の産物ではない」という結果が示されれば、データが手元にない将来の受講者でも、同じような平均の違いが生じると解釈できるのです。

このようにt検定を用いることで、得点の上昇が偶然ではないという結果が得られた場合、研修の効果は今後も同様に示されることが期待できます。研修によって、受講者のリーダーシップが平均的に高められる統計学的なエビデンスが得られるわけです。

2．t 検定の分析内容

t検定が使えるデータ３種

ここからは、t検定の具体的な分析内容を紹介していきます。分析のプロセスを見ていくということで、統計学の数式の構成についても少し解説します。

まず、t検定が使える代表的なデータの例を以下に示しています。

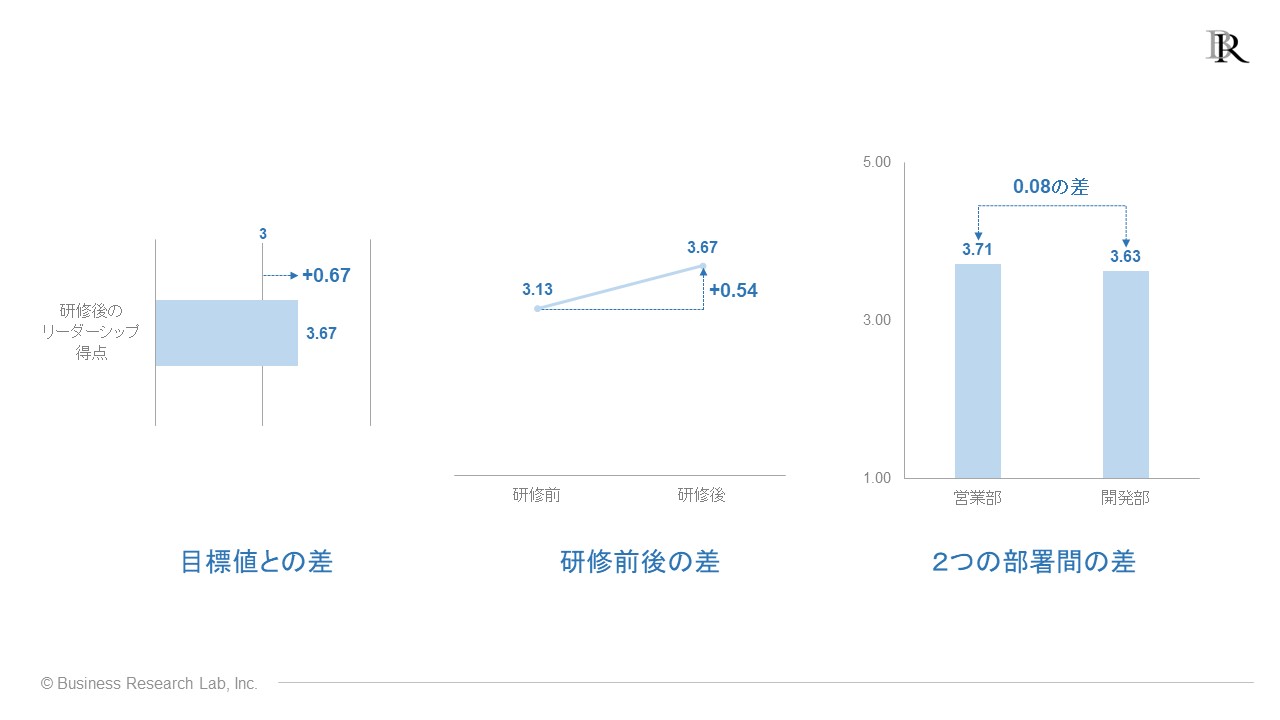
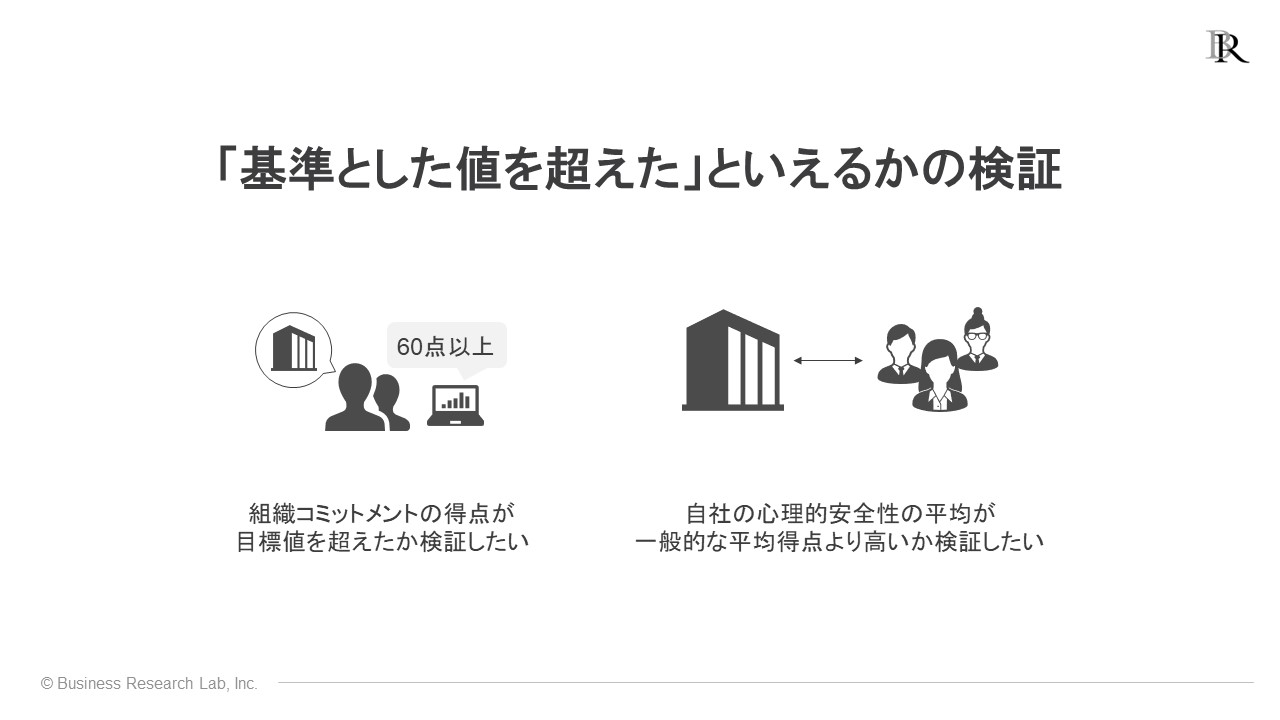
まず、得られたデータの平均と目標値との差を統計的に比較できます。少し言い換えると、「今回のサーベイで得られた平均が、基準・目標とした値を超えているか」を検証する際、t検定は使えます。

例えば、左側にあるグラフのように、リーダーシップの平均得点3.67点というデータが得られ、事前に設定したリーダーシップ得点の目標値が3点だったとしましょう。この平均得点3.67点が目標値とした3点を超えたといえるのか、t検定で検証できます。

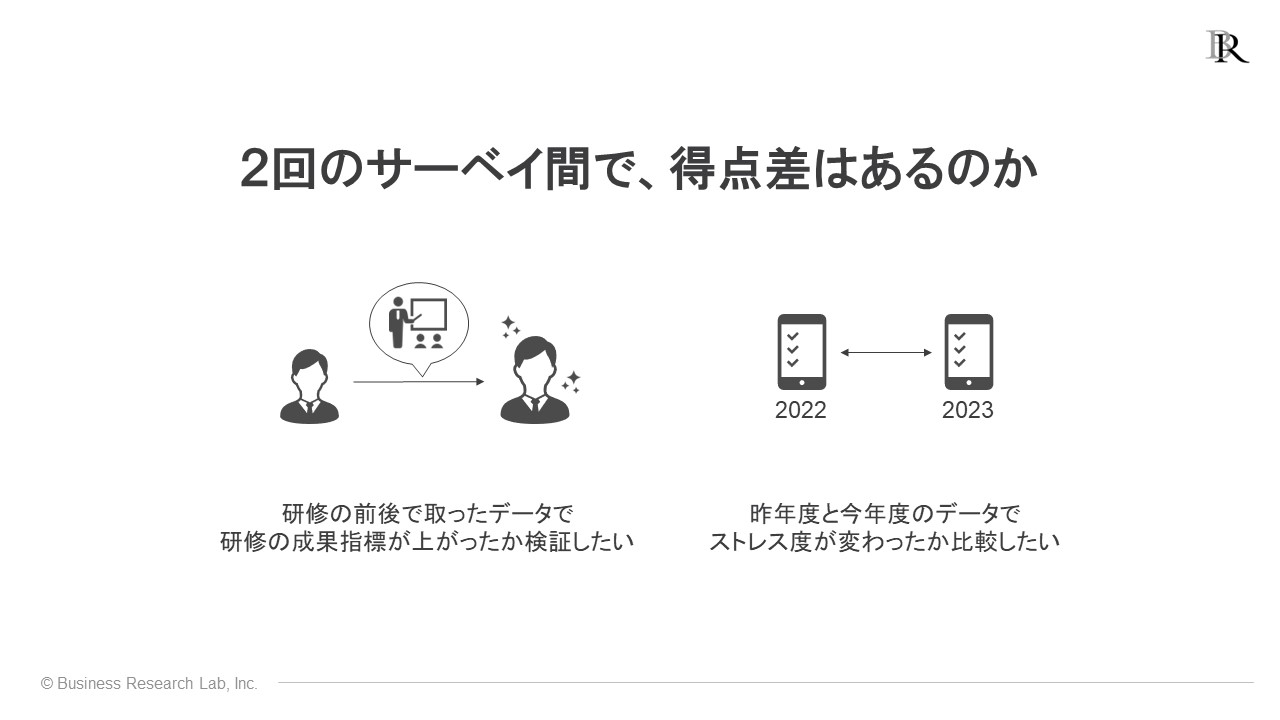
次に、２回のサーベイ間で、ある指標の平均得点に違いがあるかをt検定で検証できます。ここでは、「同じ人物が、同様のサーベイに２回回答したデータがある状況」を想定しています。

これは、研修前後の平均の比較があてはまります。例えば、先ほど示した中央のグラフのように、8名の受講生が研修前後でリーダーシップを測定する同じ質問項目に回答し、その平均得点がそれぞれ3.13点、3.67点であった状況です。この研修前後の平均得点の差異も、t検定で検証できます。

最後に、異なる２グループのメンバーそれぞれが同じサーベイに回答し、各グループの平均得点に違いがあるかも、t検定で検証できる分析枠組みです。具体的には、先ほど示した右側のグラフのように、二つの部署間（営業部と開発部）のリーダーシップの平均に違いがあるか、t検定で検証できます。

以上をやや大まかにまとめると、ある指標について得られた二つの得点に違いがあるかを統計的に検証したいシーンにおいて、t検定を使うことができます。

t検定の分析プロセス（帰無仮説検定）

次に、t検定の具体的なプロセスを見ていきます。t検定は帰無仮説検定の一つであり、統計的に有意かどうかを判断する分析枠組みとなっています[1]。

帰無仮説検定では、帰無仮説と呼ばれる仮説を最初に設定し、それに基づいて検証を進めて行きます。t検定における帰無仮説検定の手続きは3ステップあり、その概要を次に示しました。

第1ステップ：帰無仮説の設定

帰無仮説検定では、最初に帰無仮説が設定されます。何を検証したいのかが明確でなければ、分析は始まりませんので、まずはその部分を準備します。

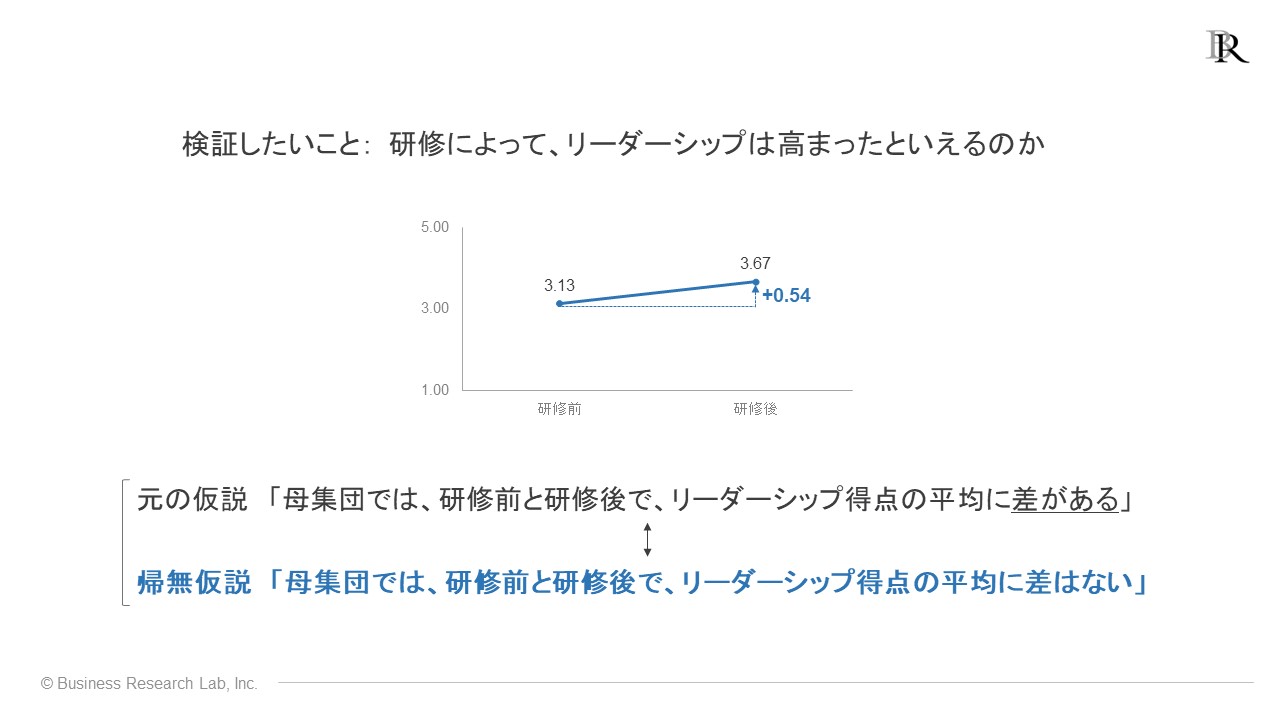
先ほどの例に基づいて説明しますが、例えば「研修によって、リーダーシップは高まったと言えるのか」という疑問を検証するためにデータを収集したとします。その結果、研修前と研修後で平均的に0.54点の得点向上が確認できた、という状況があります。

帰無仮説の設定に際して、まず、検証したいことや疑問から「元の仮説」を設定します[2]。検証したい事柄は「研修に効果があったのか」、より詳しく言えば「研修によって、リーダーシップの高さに違いが生じたのか」となります。

これを仮説として述べるなら、「研修前と研修後で、リーダーシップ得点の平均に差がある」となります。仮説はデータで検証可能となるよう、「差がある」と平均差の有無について述べるよう構成するのがコツです。

さらに、帰無仮説検定の際には、この元の仮説を母集団に対するものとして設計します。つまり、「母集団では、研修前と研修後で、リーダーシップ得点の平均に差がある」となります。

この分析の中では、母集団は「今回のサーベイでデータが測定されていない人も含めた、リーダーシップ研修の受講者全体」を指しています。サーベイに回答した受講者以外に、リーダーシップ研修に参加したけれどもサーベイには回答していない受講者や、将来の研修受講者などを含む、抽象的な受講者集団です。

帰無仮説は、元の仮説を否定する内容の仮説です。つまり、「母集団では、研修前と研修後で、リーダーシップ得点の平均に差はない」となります。

元の仮説では「平均に差がある」ことを述べた仮説だったため、帰無仮説ではそれを否定して、「平均に差がない」と述べる仮説になります。このように帰無仮説は、元の仮説で取り上げた事柄を「ない」と述べる構成になる特徴を持ちます。

第2ステップ：t値の計算

次に、t値の算出に進みます。これはt検定でｐ値と呼ばれる確率の値を計算するために必要な指標です[3]。t値は、母集団において２つの平均に差があるか否かを評価するために用いられ、その絶対値が大きいほど「母集団において、２つの平均に差がある」と見なせる指標となります。

ｔ値の計算方法について簡単に説明します。t値の計算は大まかに、「差の大きさ」となる指標を「差のばらつき」の指標で割り算することで算出します。

ｔ値の数式にはいくつかのバリエーションが存在しますが、基本的にはこの「差の大きさを、差のばらつきで割る」という枠組みは共通です。

ここで、「なぜ差のばらつきで割るのか」と疑問を抱くかもしれません。差のばらつきで割り算する理由は、サーベイで得られた手元のデータから母集団の特徴を推測するに際して、手元のデータにおける差のばらつきの程度を加味する必要があるからです。

冒頭のリーダーシップ研修の例で示したように、各々の受講者における研修前後の得点差は様々な値となるでしょう。平均的な得点差は+0.54点だとしても、その中では、得点が上昇した人もいれば、得点が変化していない人や下がった人もいます。

「研修前後のリーダーシップ得点の変化には受講者間でばらつきがある。そのデータで示された平均的な得点上昇は、偶然ではないのか」という考えが最初に浮かんだのは、まさにこの「差のばらつき」があることが原因です。

したがって、t検定において手元のデータから母集団を推測するためには、差が平均的にどの程度あったかだけでなく、手元のデータで見られた「差のばらつき」も加味して考える必要があります。t値の数式が差のばらつきで割り算するプロセスを含んでいるのは、そのためです。

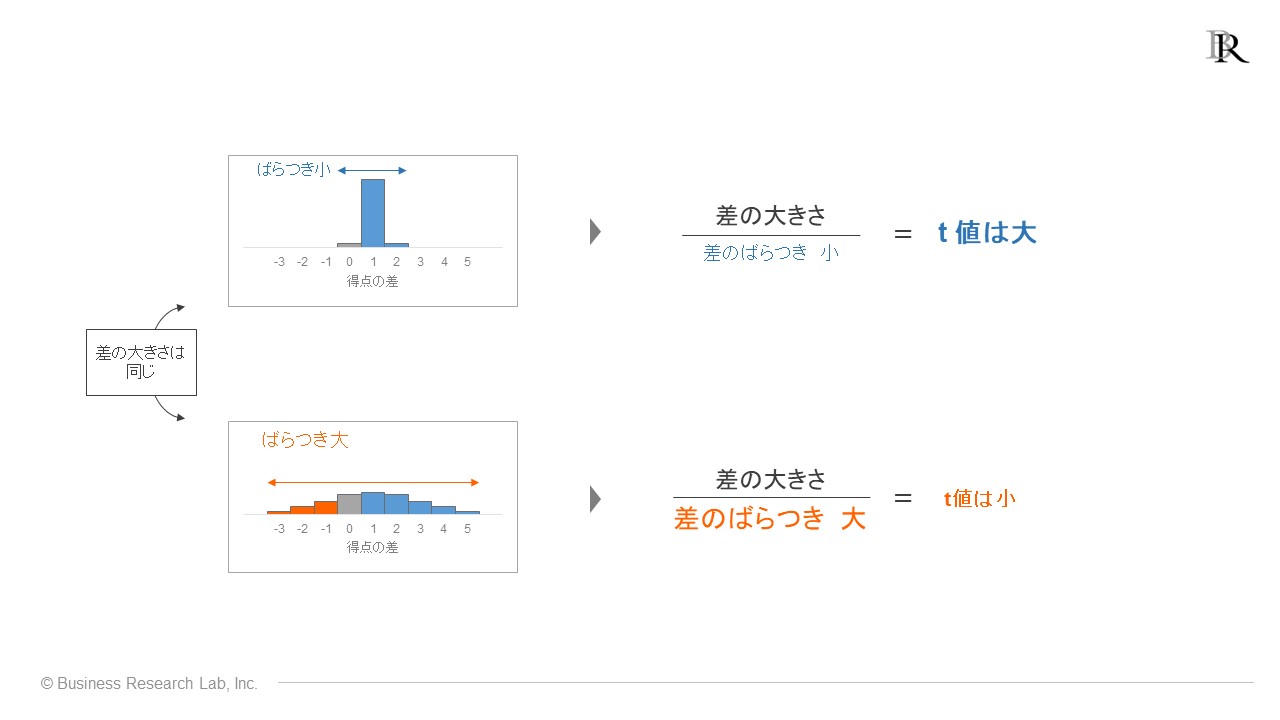
差のばらつきの割り算を含めることで、t値がどう違ってくるか見ていきましょう。以下の例では、平均的な差の大きさを1として、個々のデータの得点差がほぼばらついていない「差のばらつきが小さい」場合と、得点差の大きくばらついている「差のばらつきが大きい」場合を考えています。

例の上のデータでは、差のばらつきが小さいためt値の数式における分母の値が小さくなり、ｔ値は大きくなります。個々のデータにおける得点差データのばらつきが小さいと、t値は大きい値となることがわかります。

逆に、例の下のデータでは、差のばらつきが大きいため分母が大きくなり、ｔ値は小さくなります。個々のデータにおける得点差データのばらつきが大きいと、t値は小さい値となることがわかります。

このt値の挙動は、「手元のデータで得点差のばらつきが大きいと、そこで示された結果が確かなものか疑問を抱いてしまう」ことと、うまく対応しています。

例えば、手元のデータで個々のデータの得点差が非常にばらついていると「次のサーベイでは、結果が違ってくるかもしれない」と疑問を抱くでしょう。そのデータで示された平均の差は、なかなか信用できません。これは差のばらつきが大きい状況であり、そういったデータのt値は小さな値となります。

一方で、ばらつきが少ないデータならば、「次のサーベイでも同じような結果が出ると期待できそう、データで示された平均の差は確実なものだろう」と感じられます。これは差のばらつきが小さい状況であり、そのデータのt値は大きい値となります。

t値は値が大きいほど「母集団に平均的な得点差がある」と見なせる指標であることを踏まえると、現実場面の直感的な判断に対して、算出されるt値の大きさがうまく対応しているとわかります。

このようにｔ値は、得られたデータにおける差のばらつきを加味することで、母集団における平均差を適切に評価できるように設計されています。ここがｔ値の数式のポイントです。

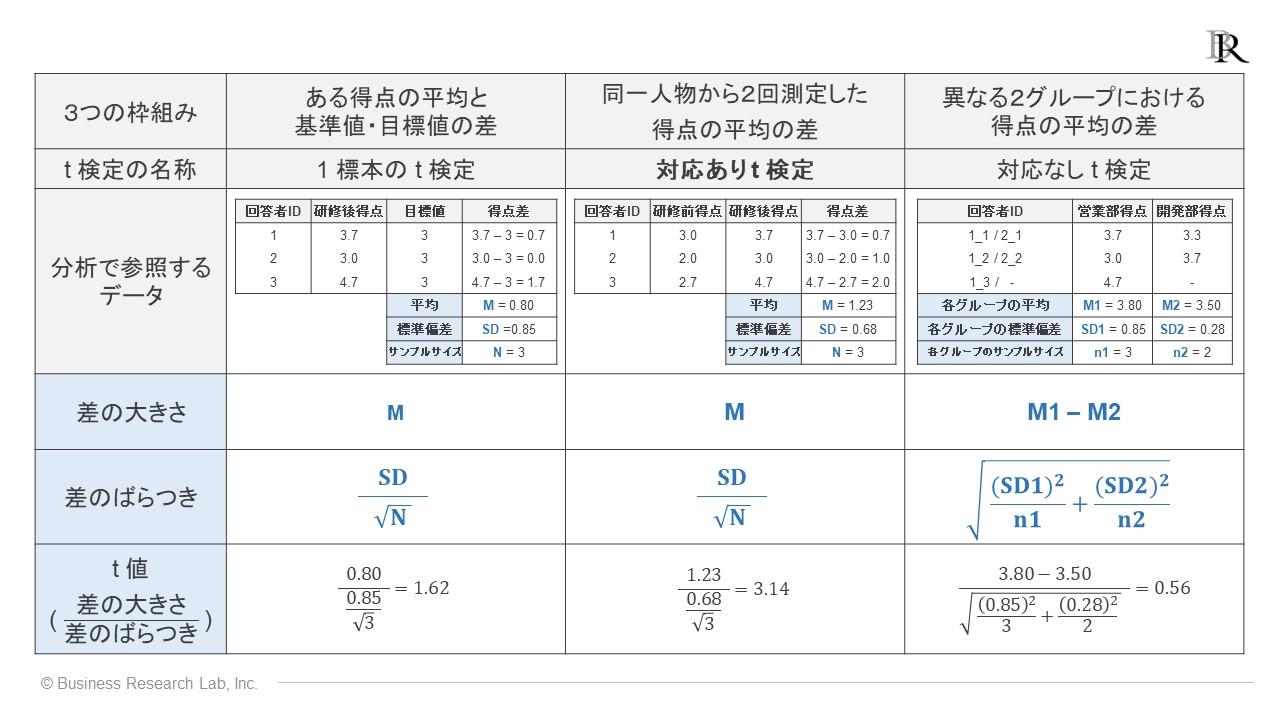
以下は、t検定の3つの枠組みそれぞれにおける、t値の数式をまとめたものです。t値はプラスとマイナスどちらの値も取りますが、絶対値で判断していただいて差し支えありません[4]。

データの枠組みが違うと差の大きさやばらつきの捉え方が変わるため、数式も違ってきます。なお、込み入った話題になるため詳細は割愛しますが、基準値・目標値との差の検証と、同じ回答者から２回測定したデータにおける差の検証の数式は、同じものになります。

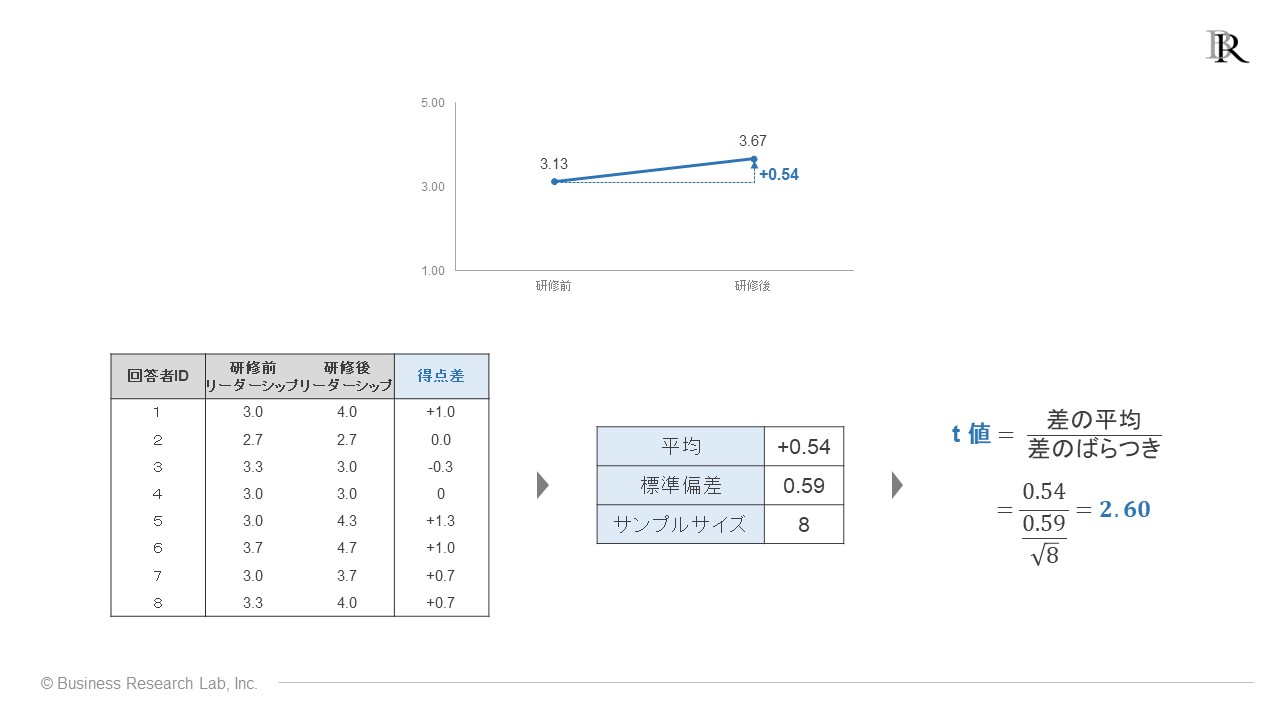
最初に出した架空例のグラフのデータについて、ｔ値を計算した例をお示しします。

左から順に、ローデータ、差の平均とばらつきの計算に必要な平均、標準偏差、サンプルサイズの情報、そしてt値の計算となっています。この例では、差の大きさと差のばらつきを算出してt値を計算した結果、t = 2.60という値が得られました。

実践的には、t値は統計ツールで自動的に計算されるので、数式の暗記が絶対に必要なわけではないです。しかし、t検定がどういったことをしているかを学んでいただく上で、t値が数式で取り上げる事柄と計算の流れをおおまかにご理解いただくのは有効でしょう。余裕のある方は、ぜひこの点も知っていただければ幸いです。

第3ステップ：p値の計算

では3つ目のステップとして、p値の算出に移ります。帰無仮説検定は、このp値を用いて「手元のデータで示された結果が偶然の産物でない、母集団の特徴だ」と言えるかを判断します1。

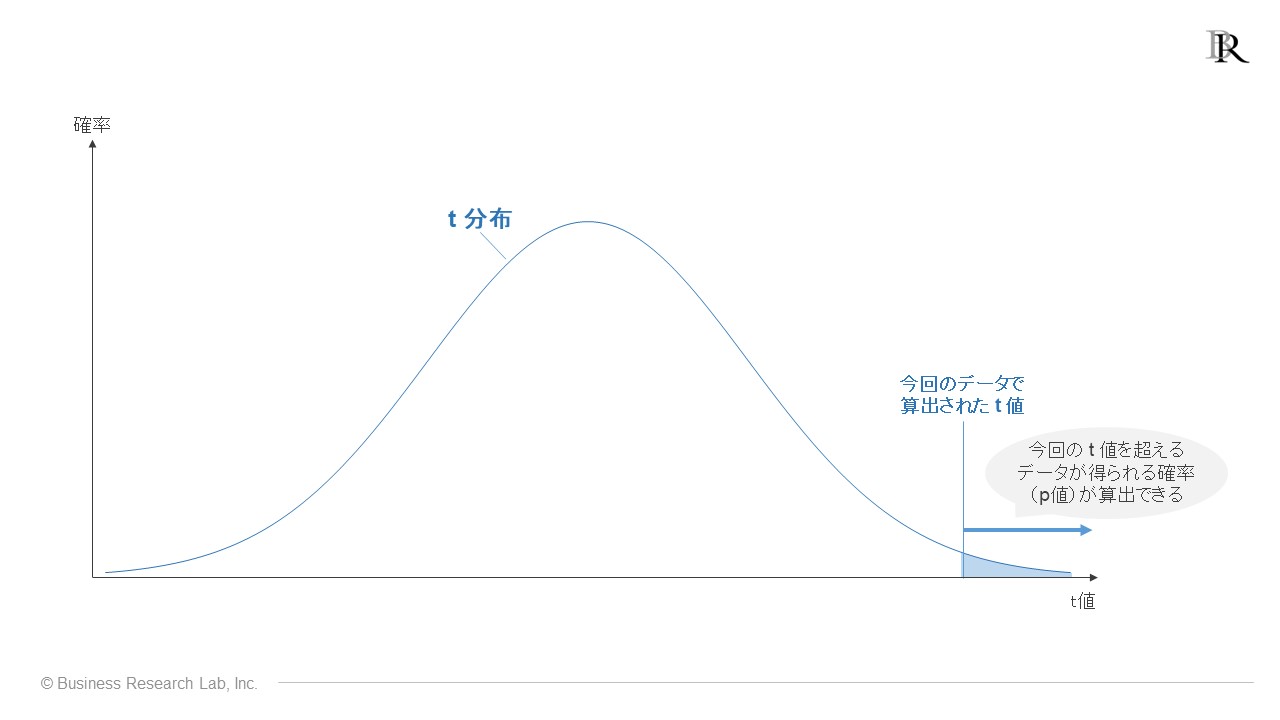
帰無仮説検定においてp値を算出するには、t値からp値を導き出すグラフが必要となります。t検定で使うこのグラフは「ｔ分布」といいます。

t分布にt値をあてはめてp値を算出するプロセスはこのグラフで表されるのですが、やや複雑なので、ここでは簡単に説明します。

t検定におけるp値は、「母集団では、平均に差がない」とする帰無仮説が正しい前提において、今後同じようにサーベイを実施した際、今回得られた結果を超えるようなデータが新たに得られる確率を指します。今回得られた結果とは、t値のことです。

t分布は、特定のt値に対応したその確率の情報を表すグラフであり、t分布にt値をあてはめて計算することで、p値が求められるわけです[5]。

こうして算出されたp値を用いて、帰無仮説が棄却できるかどうかを判断します。

具体的には、ｔ値から算出されたp値が5%（0.05）未満であれば、手元のデータで示された平均差は統計的に有意であると認められ、帰無仮説を棄却して元の仮説を支持します。他方、p値が5%以上であれば、帰無仮説は棄却されず、判断は保留されます。

先ほどの例で計算したt値について、p値を計算し、統計的に有意か否か判断するプロセスを追ってみましょう。手元のデータから算出されたｔ値がt = 2.60で、このｔ値に対するp値をt分布にあてはめて算出したところ、p値は0.035（3.5%）だったとします。

この場合、p値は5%未満であるため、「統計的に有意である」と認められます。統計的に有意だと認められた場合、帰無仮説が棄却されて元の仮説が支持されます。つまり、「差がない」帰無仮説が棄却され、「差がある」といった元の仮説が支持されます。

リーダーシップ研修の例でいえば、「母集団では、研修前と研修後で、リーダーシップ得点の平均に差がある」という元の仮説に対して、帰無仮説は「母集団では、研修前と研修後で、リーダーシップ得点の平均に差はない」でした。

p値による判断を経て「統計的に有意」だと認められると、帰無仮説が棄却されて元の仮説が支持されます。つまり、「母集団では、研修前後でリーダーシップの平均得点に差がある高い」という元の仮説が支持されます。

この元の仮説支持について、手元のデータで研修後のリーダーシップ得点の平均の方が高いことも踏まえると、「母集団では、研修後の方が研修前より、リーダーシップ得点が高い」と判断できます。このようにして、得られたデータで示された結果が偶然でなく、母集団にもあてはまる結果だと主張できるのです。

 

これが、t検定全体のプロセスになります。t検定を用いれば、母集団において二つの得点の平均に差が存在するかどうかが統計的に検証されます。研修前後の平均差の例では、t検定で統計的に有意だと認められれば、「今後も、研修後の平均的な得点上昇が期待できる」という証拠が得られたといえます。

3．t 検定の実践例

ここからは、t検定の3種類の枠組みを土台に、t検定の具体的な使い方を紹介します。t検定の計算プロセスは、帰無仮説の考え方を除いて、どの枠組みでも先ほど紹介した展開と同じです。

そこで、以降ではそれぞれの枠組みがどういった場面で使えるかと、帰無仮説とその前にある元の仮説の設定について取り上げていきます。

目標値との比較：1標本のt検定

一つ目の枠組みは、何らかの目標値、基準値と比べるアプローチです。これは、「1標本のt検定」と呼ばれます。この枠組みでは、ある指標についてサーベイなどで得られたデータの平均と、分析者が設定した基準値との間に違いがあるかを統計的に検証します。

例えば、組織コミットメント得点について、事前に目標値を60点と設定している場合、サーベイで得られたデータの組織コミットメントの平均と、目標値である60点との差を比較したいとき、このアプローチが使えます。

t検定を経て、その結果から、得られたデータの組織コミットメント得点の平均と目標点の差が統計的に有意だと認められ、組織コミットメントの平均の値が60点を超えていれば、「目標点数を超えた」と主張できます。

他にも、従業員の心理的安全性に注目し、一般的な平均得点が3.13点という調査結果が公表されていたとします。その値を基準にして、自社の心理的安全性の平均がそれより高いか比較したいとき、このアプローチが使えます。

例えば、自社の平均得点3.62点と算出された際、その値は一般的な平均得点3.13点より高いといえるかについて、２つの得点の差を1標本のt検定で検証した結果、統計的に有意だと認められれば、「自社の心理的安全性の平均は、一般的な平均より高い」と主張できます。

1標本のt検定における元の仮説は「母集団では、ある指標の平均得点は、（基準値・目標値とした）〇点と差がある」、帰無仮説は、「母集団では、ある指標の平均得点は、（基準値・目標値とした）〇点と差がない」となります。

例えば、先ほどのリーダーシップ研修において、研修後のリーダーシップ得点が3点を越えることを目標値としていた中で、実際に測定された研修後リーダーシップの平均得点が目標点を超えているか確かめたいとしましょう。

その場合、1標本のt検定における元の仮説は「母集団では、研修後のリーダーシップの平均得点は、3点と差がある」帰無仮説は「母集団では、研修後のリーダーシップの平均得点は、3点と差がない」となります。

この帰無仮説を基にt検定を行えば、その結果から研修後のリーダーシップ得点の平均が目標とする3点を超えたと言えるか否か、統計的な検証結果を土台にして述べられるようになるのです。

前後の得点の比較：対応のあるt検定

2つ目の枠組みは、同じ回答者から2回測定したデータを比べるアプローチです。この枠組みでは、対応ありt検定と呼ばれるものを使います。

これを用いる場面としてよくあるのは、研修前後である指標の平均得点を比較する場合です。具体的には、研修の前後で、同じ参加者からある指標のデータを2度取り、その平均に違いが生じたか確かめたい場面で、このアプローチが使えます。

例えば、キャリア意識を高める目的の研修を行った場合、研修前と研修後でキャリア意識の平均得点が高まったといえるのかを調べる、といった具合です。

他にも、過去のストレスチェックデータと現在のデータを比較する場面があります。2022年と今年度に実施したストレスチェックのデータを、同じ社員データを紐付けて比較することで、ストレスレベルが時間を経て変わっているか確認できます。

このアプローチの大きな特徴として、データ分析の上では1回目と2回目のサーベイデータにおいて「平均に差があるか」と差の有無を検証していますが、その解釈として、1回目から2回目にかけて、「平均が上がった、平均が下がった」など、変化を主張できることがあります。

「同じ人物から2回測定したデータにおいて、ある指標の平均は高まったといえるのか」といった得点の平均的な変化について検証したい場合は、この枠組みを採用することになります。

なお、このアプローチにおける元の仮説と帰無仮説の例は、先ほど挙げた「リーダーシップ研修における研修前後の平均差のt検定」が該当するため、ここでは省略します。

異なる属性間の比較：対応のないt検定

3つ目の枠組みは、2グループに分かれた異なる回答者のデータを比べるアプローチです。この場合は、対応なしt検定と呼ばれるものを使います

例えば、営業1課と営業2課で、ワークエンゲージメントに違いがあるかを検証したいとき、をこのアプローチが使えます。それぞれの課でワークエンゲージメントのデータを測定してあれば、1課と2課の平均得点の差を検証することで、違いがあるか統計的に検証できるわけです。

あるいは、新卒採用者と中途採用者において、どちらのほうが上司との関係が良いかといった比較でも、このアプローチが使えます。新卒採用者と中途採用者それぞれで上司との関係の良さを測定し、平均得点の差をこのアプローチで検証することで、どちらの方が上司との関係が良いか統計的に確かめることができます。

対応のないt検定における元の仮説は「母集団では、グループAとグループBにおいて、ある指標の平均得点に差がある」、帰無仮説は、「母集団では、グループAとグループBにおいて、ある指標の平均得点に差がない」となります。

例えば、研修後のリーダーシップ得点を営業部と開発部で比べるならば、元の仮説は「母集団では、営業部と開発部において、リーダーシップ得点の平均得点に差がある」、帰無仮説は、「母集団では、営業部と開発部において、リーダーシップ得点の平均得点に差がない」となります。

この帰無仮説を基にt検定を行えば、研修後のリーダーシップ得点が営業部と開発部でどちらの方が高いのかについて、統計的な根拠をもって述べることができるようになります。

4．t 検定の注意点

正規分布していないデータには使用できない

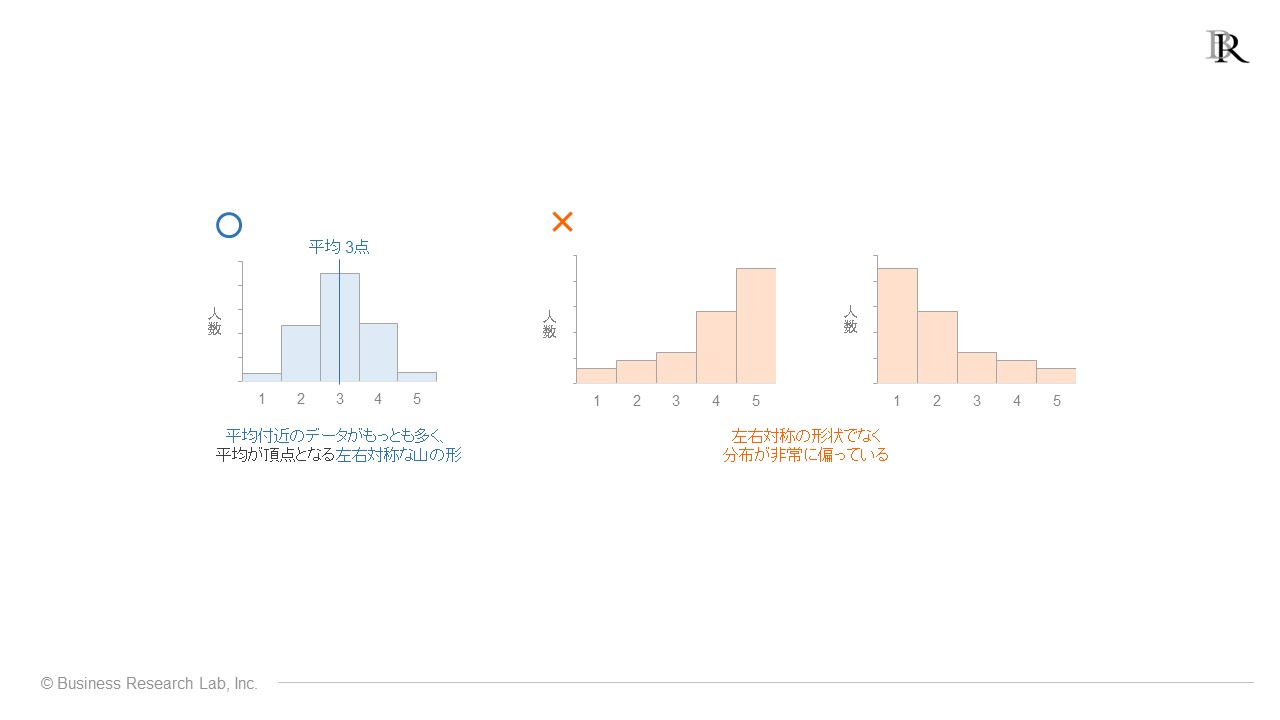
最後に、t検定に関する注意点をまとめます。1つ目は、正規分布してないデータに対してt検定は使えないということです[6]。正規分布とは、以下に示した図のうち、左側の青いグラフが相当します。

具体的には、平均値に近い得点を答えた人数が多く、平均値から離れるほど人数が減っていき、結果として左右対称の山形のグラフになっているものです。このようなグラフの形状となる回答データ分布を正規分布といい、多くのアンケートの回答は、この形状を示します。

対して、正規分布していないの例は、橙色のグラフです。このように、高得点・低得点に回答者の人数が偏ってしまったデータは正規分布していない代表的な例です。

正規分布ではないデータでも、計算上はt検定の結果を出せますが、あまりに正規分布から逸脱しているデータだと、その結果は不正確な可能性があります。回答分布があまりに偏っているデータには、t検定はあまり使わない方がよいでしょう。

t検定における結果は「差の大きさ」を表しているわけでない

2つ目の注意点は、t検定において統計的に有意だと認められたとしても、その結果から「差が大きい」といった量的な主張はできないことです。有意な平均差は、あくまで相対的な大小比較に過ぎません。

統計的に有意だと認められた後のプロセスでは、帰無仮説を棄却して元の仮説を支持します。そこでは「平均に差がない」という帰無仮説が棄却されて「平均に差がある」と差が存在することが支持されたにすぎず、平均の差が大きいことは特に述べていないのです。

このように、t検定によって有意であると示された2つの平均得点の違いは、あくまでも「一方の平均が、もう一方よりも相対的に高い」ことまでしか示されていません。従って、得点の差の大きさについては、実際の回答データで見られる平均得点がどのぐらいだったかを見て考える必要があります。

例えば、会社に注意が必要な例として、以下の図をご覧ください。この仮想データで、研修後と研修前の得点をt検定で比較した結果、「研修後に、キャリア開意欲得点は高くなった」という解釈ができたとします。

ただしこの時、t検定の結果は、「キャリア開発意欲がとても高くなった、抜群に伸びた」といった、得点上昇の大きさまで検証してはいません。この得点上昇が大きいと言えるかは、実際に示された0.36点の上昇をどう意味づけるかの問題で、それはサーベイ実施者・分析者に委ねられます[7]

そのため、t検定を実施する際は、統計的に有意といった結果だけに注目せず、その後に実際に得られたデータの得点もよく確認する習慣をつけるようにしましょう。

最後に

本日はt検定を紹介しました。2グループの平均差を分析し、統計的に有意かを判断することで、測定されたデータで示された平均差が偶然の産物でない確実なものか、統計的に評価できるようになります。

また、t検定を学ぶことで、データの捉え方を身につけられます。ひとつは、実際に測定したデータで示された平均の差は、本来捉えたい回答者全体の特徴とは別物と考える視点です。

これは推測統計を扱う上での基本であり、「統計的に有意」を解説したセミナーでもお伝えしたポイントになります。手元で得られたデータは、あくまでその時データが取れた回答者の特徴を反映したものであり、本来捉えたいサーベイ対象者全体の特徴は別立てて考える必要があるということです。

t検定では、それを検証する方法を一つ学んでいただきましたが、この「実際に測定されたデータは回答者の特徴、母集団の特徴は別で推測すべきだ」と考える視点は、データ分析を学ぶ上でぜひ意識しましょう。

加えて、２つの得点間の差を捉える視点として、3つの枠組みがあることを知るのも有効です。ある指標のデータがどのような状態なのか他のデータと比べて考えたいとき、この3つの捉え方があると知っていると、多様な視点での検証が可能になります。

t検定に限らず、データ分析の手法を知ることは、「データ分析で何が検証できるのか」「データをどのような視点でひも解けば組織の課題にアプローチできるのか」といった、データの活かし方を学ぶことにもつながります。

本日の解説内容から、t検定の分析手法だけでなく、データの捉え方や活かし方の観点も学んでいきましょう。

Q&A

Q: 比較したい部署が3つ以上あるときはt検定を繰り返せばよいのか？

3つ以上のグループ間で比較を行いたい場合、t検定を繰り返す方法は統計学的に推奨されていません。これは検定の多重性と呼ばれる問題で、何度も検定を繰り返すと、数を打てば鉄砲は当たるがごとく、統計的に有意な平均差が偶然に認められてしまう可能性が高まります。

このような課題を解決するためには、三つ以上のグループを比較する際には「分散分析」という枠組みがあります。例えば、営業部、開発部、総務部など、三つ以上の部署を比較したい場合は、まず分散分析を使用することが推奨されています[8]。

Q: 回答者の人数はt検定の結果に影響するか

回答者の人数、すなわちサンプルサイズは、t検定の結果に影響を与えます。具体的には、サンプルサイズが大きくなるほど、p値が小さくなって有意な結果が出やすくなる特性があります。

回答者の人数が非常に多い場合、t検定の結果はたいてい統計的に有意になり元の仮説が支持されるので、「t検定の結果が統計的に有意かどうか」という部分は、あまり意味がありません。そのときは、実際の平均差など、具体的な数値を確認することがより一層大切になります。

Q: 少ない人数での分析結果が有意だった場合の結果はどう見るべきか

まず、先ほどと逆の話になりますが、回答者の人数が少ないと、ある程度の平均差があったとしても「統計的に有意である」と認められにくくなります。その状況で有意な平均差だと認められているならば、平均差があると主張しても差し支えないと考えられます。

ただ、注意すべき点として、少ない人数による母集団の推測は、推測精度が低くなる限界があります。そのため、統計的に有意だと認められて「差は存在する」と主張できても、その差の大きさがどの程度かについて、あまり正確に検証できていないことは意識しましょう。

また、その少ない回答者が、想定する母集団と合っているかも重要です。帰無仮説検定における母集団は回答データから推測されるため、回答者が偏っていれば、想定される母集団もその回答者が代表となるような集合になります。

分析結果を解釈する際、「どのような社員について、推測しようとしているのか」という母集団の想定をイメージした上で、その少人数回答が想定に対して偏っていないか、確認するのも良いでしょう。

 

脚注 

[1] 推測統計や帰無仮説検定、p値の考え方については、当社コラム「人事のためのデータ分析講座『統計的に有意』を学ぶ（セミナーレポート）」で詳しく解説しています。

[2] 統計学では、この仮説は「対立仮説」と呼ばれます。

[3] 帰無仮説検定では、後述するp値と呼ばれる指標により「統計的に有意か」を判断するプロセスを含み、p値を計算するために用いられる指標を検定統計量と呼びます。t値はt検定にて用いられる検定統計量です。そのため、第2ステップ「t検定におけるt値の算出」は、帰無仮説検定全般に向けてより一般化すると「p値算出に向けて、検定統計量を計算するステップ」となります。

[4] 厳密には、片側検定・両側検定と呼ばれるt検定の中のバリエーションにおいて、片側検定の場合はt値が正負のどちらかであるかに意味があります。しかし、一般にt検定を活用する際は両側検定を用いることから、ここでは絶対値で問題はないとしています。

[5] 正確には、ここで参照されるt分布の形状を定める「自由度」と呼ばれる指標についても計算が必要であり、この計算もt検定の３枠組みで違ってきます。自由度を巡る議論は難解であり、Welchの補正を含めて分析ツールが自動処理することもあるため、この解説では割愛しています。この話題は、別コラムで解説する予定です。

[6] なお、t検定は正規性の仮定をいくらか満たさないデータでも、ある程度問題なく推定ができる頑健性があると言われています。しかし、一般的な組織サーベイで得られるデータは、サンプルサイズや測定内容の都合でその頑健性が活きづらい状況になることが多く、念のため注意点に取り上げています。

[7] 差の大きさを統計的に評価する「差の効果量」と呼ばれる指標もあります。詳しくは、当社コラム「効果量とは何か：『差の大きさ』を評価する指標」で解説しています。

[8] 分散分析の詳しい内容については、当社コラム「一要因分散分析とは何か」で解説しています。

---

登壇者

能渡真澄
株式会社ビジネスリサーチラボ フェロー。信州大学人文学部卒業、信州大学大学院人文科学研究科修士課程修了。修士（文学）。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を、他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており、通常では捉えることが困難な、様々なデータの背後にある特徴や関係性を分析・可視化し、その実態を把握する支援を行っている。