2023年4月21日
効果量とは何か:「差の大きさ」を評価する指標
データサイエンスを活用したエビデンスに基づく意思決定に注目が集まっています。その中で、統計学的な意思決定の手法がますます活用されるようになってきました。特に用いられることが多い手法のひとつが「帰無仮説検定」です。帰無仮説検定とは、「統計的に有意である」か否かを判断する統計学的手法のことで、着目した得点差や関連の強さに関して、「差がない/関連がない」といった帰無仮説を検証する検定を指します(Cramer & Howitt, 2004)。これを活用することで、組織サーベイで取得したデータの集計値が示す結果に新たな判断材料を加え、より有効な意思決定につなげることができます。
その一方で、帰無仮説検定の限界はあまり意識されていません。人事領域にも少しずつ浸透してきた帰無仮説検定の考え方ですが、この手法には考慮すべき限界があるのです。
本コラムでは、初めに「統計的に有意」の意味を簡単に見直しつつ、その限界点を指摘します。その上で、限界を乗り越える統計指標のひとつとして「効果量」を紹介していきます[1]。
「統計的に有意」の意味とその限界
帰無仮説検定は、検証したい仮説に対して、真逆となる仮説(帰無仮説)を設定し、検証したい仮説が支持されるか否かを検証する分析枠組みです。
帰無仮説を前提として、取得したデータで示される結果を超えるような新たなデータがどの程度の確率で取得できるものかを検証し、その確率(p値)が小さければ、帰無仮説を棄却して検証仮説を支持するという判断を下します。
例えば、「研修後の方が、研修前よりも学習量が多くなる」という仮説を検証する際、帰無仮説は「研修前後で、学習量に違いはない」となります。p値が基準値より小さければ、帰無仮説を棄却し、最初の仮説を支持します。
ただし、帰無仮説検定には、あまり意識されない問題が存在します。本コラムでは、組織サーベイ後の意思決定に影響する2つの問題を取り上げます。
問題1.差や関連が「どの程度」あると言えるかわからない
帰無仮説検定のプロセスを見ると、最終的な判断において、「帰無仮説の棄却→検証したいことから構築した元の仮説の採択・支持」としています。ここでポイントとなるのは、検証したい仮説を採択した根拠が、帰無仮説の棄却である点です。
帰無仮説は、「研修前後で学習量に、差はない」や「学習量と業務パフォーマンスの間に、相関はない」といった内容です。これが棄却されることで、検証したい仮説である「学習量は増えている」や「2指標の間に相関がある」を採択・支持しています。
ここで、よく考えてみると、帰無仮説の棄却は「差がない」「相関がない」という帰無仮説を退けただけです。つまり、「”差がない”とはいえない」「”相関がない”とはいえない」と述べているだけになります。
したがって、具体的にどの程度の差や相関があるのかについて、帰無仮説検定は何も言及していません。先ほどの研修前後の学習量の差についても、有意な結果が示されたからと言って、それは大きな差なのか、はたまた小さな差なのかについては、何も述べていないのです。
統計的に有意な結果だと示されただけでは、「研修により、学習量に”大きな差”が出た」と結論できないことが、ひとつめの問題です。
問題2.サンプルサイズが大きいと、統計的に有意な結果であると示されやすい
もうひとつの問題として、帰無仮説検定は、サンプルサイズ(回答者数)が大きいほど「統計的に有意」であると示されやすい特徴があります。
サンプルサイズが大きいほど、差や関連の検証精度が高まるため、わずかな差や関連がある程度でも「統計的に有意」だと示されやすくなるのです。その結果、実質的に意味がないような差や関連でも「差がある」「関連がある」と示されることがあります。
サンプルサイズによる帰無仮説検定の結果の違いを、無相関検定で確認してみましょう。無相関検定とは相関係数に対する帰無仮説検定であり、「2指標の間に相関がある」と言えるか否かを、帰無仮説「2指標間の間に相関はない」と設定し、帰無仮説検定する方法です。
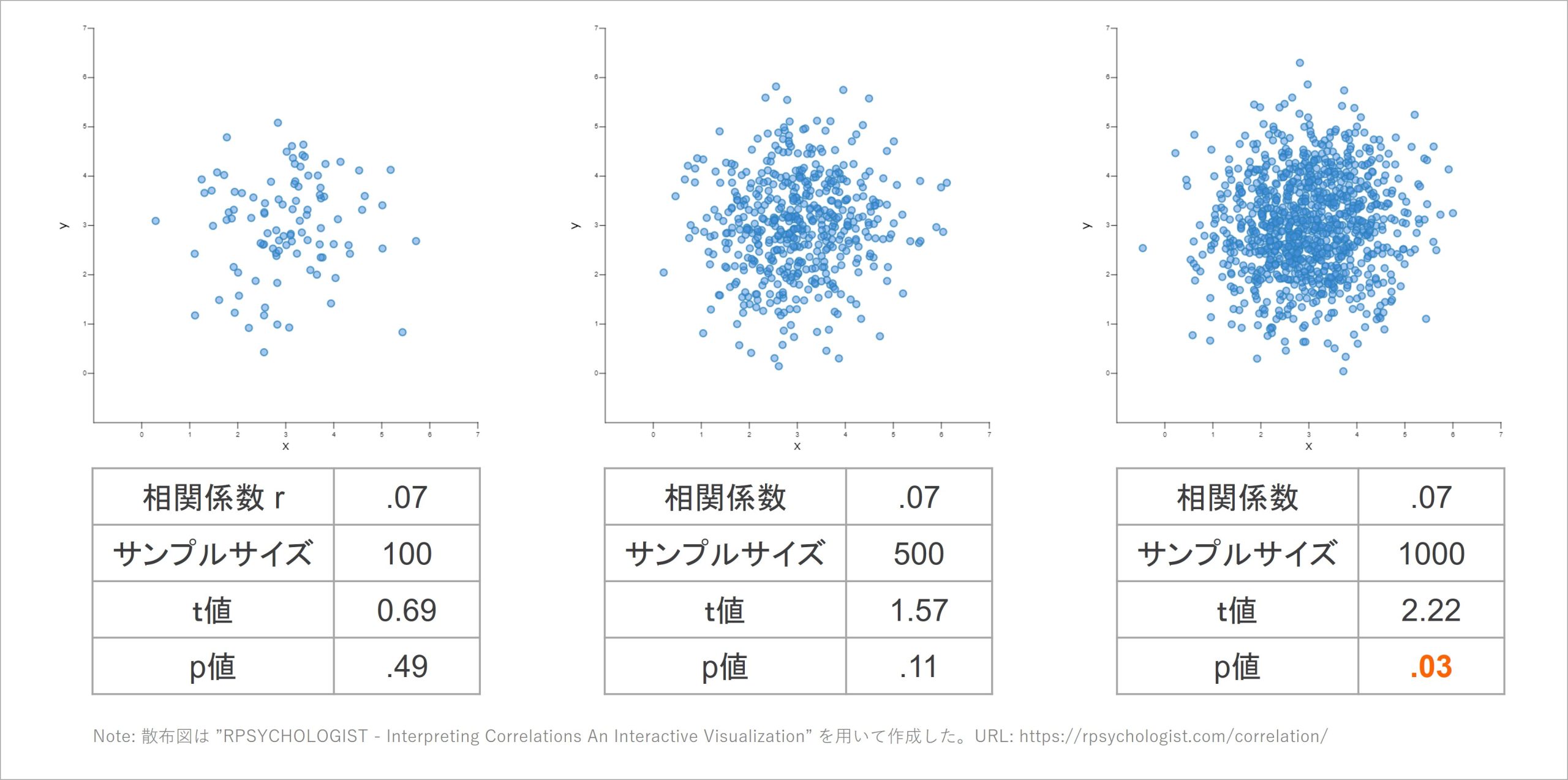
ここでは、サンプルサイズが100名、500名、1000名である3つのデータセットを想定し、全てのデータで2指標間の相関係数がr = .07である状況を想定します。以下の散布図でも可視化されますが、相関係数r = .07は2指標の得点間がほとんど対応していない状態となる程度の相関です。
どのサンプルサイズの散布図でも、2指標の得点間に対応関係はないように見えます。「一方の指標の得点が高いと、もう一方の得点も高い」といった直線的な関係が、これらのグラフからは見て取れません。
しかし、無相関検定で算出されたp値を見ると、サンプルサイズが1000の場合ではp = .03と5%を下回り、統計的に有意な相関であると認められています。その結果だけでいえば、「2つの指標の間には、統計的に有意な正の相関が認められた」と主張することは可能です。
しかし、サンプルサイズ1000のこの散布図を見て「2つの指標の間に、一方の値が高いとき、もう一方の値も高い相関関係がある」と主張する人はいないでしょう。そのような散布図でも、回答者を1000名集めたデータであれば、「統計学的に有意な正の相関」だと示されます。
これは、サンプルサイズが大きいことで精度が高まった結果として生じた現象です。無相関検定は帰無仮説「2指標間の相関は0」を棄却できるか否か検証しますが、その検証精度が高すぎるゆえに、r = .07とわずかに0より大きい程度でも「相関が0とはいえない」と判定され、統計的に有意な相関だと示されてしまうのです[2]。
この問題を言い換えるならば、「サンプルサイズが非常に大きい組織サーベイでは、帰無仮説検定は実質的に意味がなくなる」となるでしょう。
このように、帰無仮説検定はその統計学的性質から、2つの問題を常に抱えています。帰無仮説検定も万能ではなく、限界があるのです。
効果量とは
帰無仮説検定が抱えるこの種の問題は、結局のところ、「差や関連の大きさは、どのように評価すればよいのか」というところに行き着きます。帰無仮説検定に加えて、組織サーベイで示された得点の差異や関連性の強さがどの程度の大きさなのかを評価できれば、この問題が解消できます。
それを果たす統計指標として、「効果量」(effect size)があります。効果量とは、「母集団に現れるであろう、差や関連の大きさ」を表す指標です(Ellis, 2010)。
効果量によって、各指標で現れた差や関連の大きさを一律化された基準で表すことができ、それらがどの程度の大きさなのか評価しやすくなります。帰無仮説検定では把握できなかった「差や関連がどの程度あるのか」の情報が得られるようになるのです。
効果量には様々なものが存在しますが[3]、それらはd族効果量とr族効果量の2つに大別されます(Rosenthal, 1994)。本コラムでは、差の大きさについて評価するd族効果量について紹介します。
差の効果量 d族効果量
d族効果量は、2つのグループ間でどの程度の違いがあるかを表す効果量です(大久保・岡田, 2012)。組織サーベイでいえば、例えば、一般職と総合職の組織コミットメントの得点差に関して算出されるのが、この効果量となります。
あるいは、目標とする組織コミットメントの値に対して回答者の平均的な値がどの程度だったかといったことも、d族効果量で検証ができます。組織コミットメント平均得点から目標とする得点を引き算することで差の大きさを算出できるため、この効果量を用いた検証が可能です。
なお、営業部・人事部・経理部の比較のように、3個以上のグループ間で比較したい場合もあるでしょう。この場合は、「営業部と人事部の差」「営業部と経理部の差」「人事部と経理部の差」のように、2グループ間の比較を繰り返すことになり、結局のところ2グループ間の比較になります。
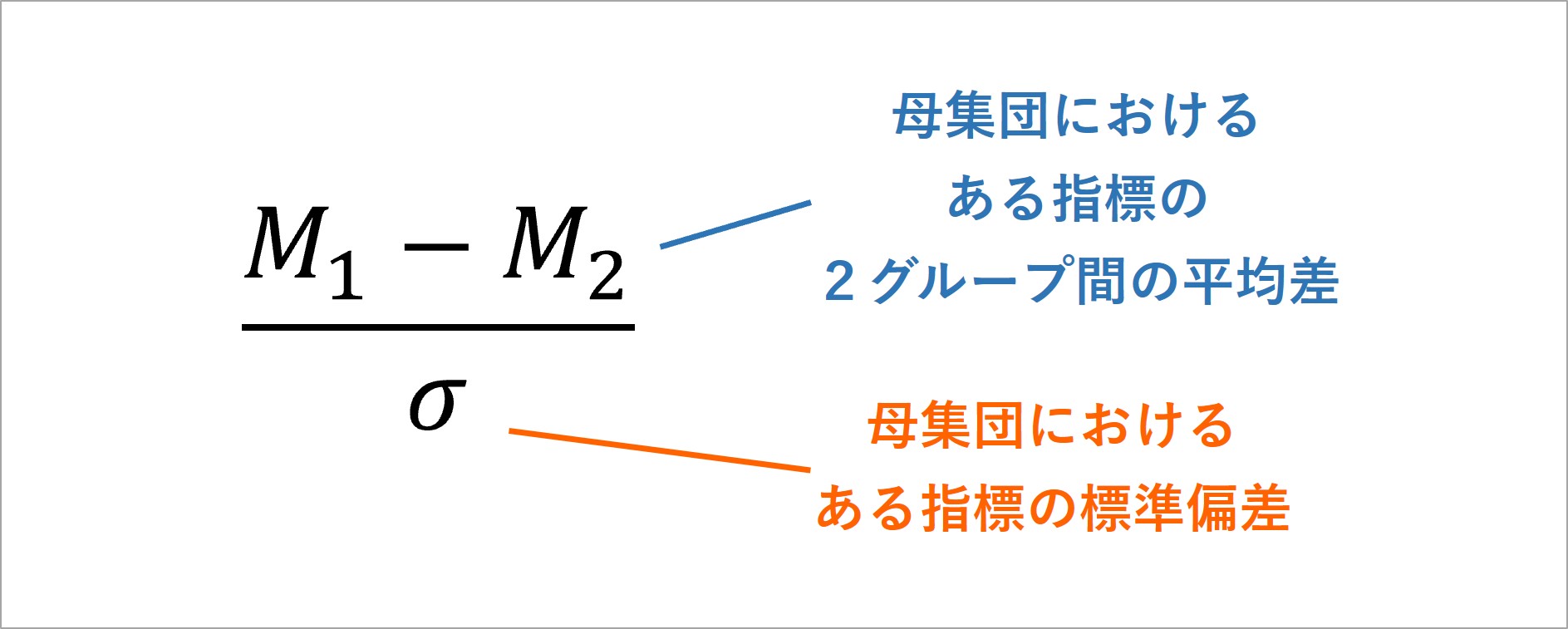
本コラムでは、d族効果量の中でも特に代表的な、「ある指標の得点における、2グループ間の差の大きさ」を表す効果量dについて解説していきます。効果量dの基盤となるアイデアは、Cohen(1962)により提唱された図 2の式です。
この式では、母集団に存在する2グループの得点差を、母集団における標準偏差で割り算しています。
差の大きさを表す効果量ですから、この式の分子では、2グループ間の得点差を取り上げています。この式のポイントは、その値を標準偏差で割り算していることです。その理由は、標準偏差(データのばらつき)が異なる指標では、得点の大きさの意味が異なるからです。
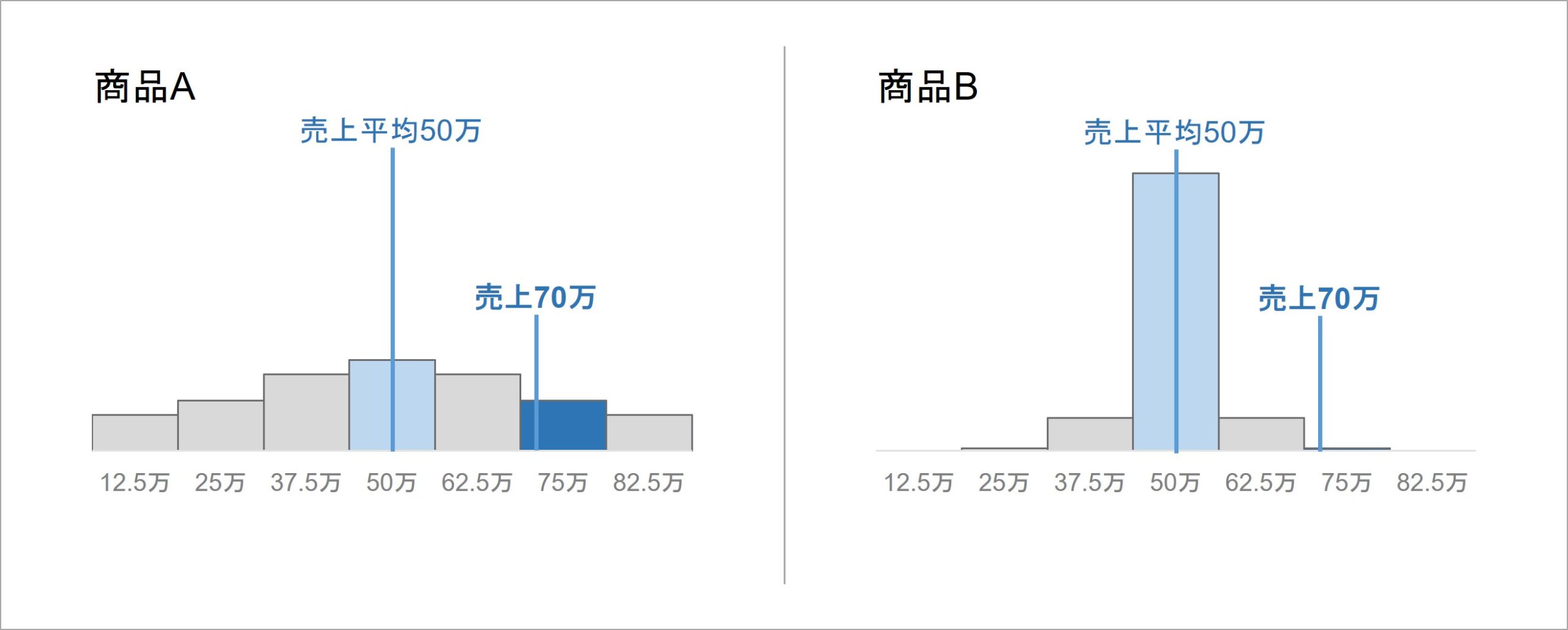
例えば、2種の商品A, Bの売上成績を評価する場合を考えてみます。2つの商品について、全営業担当者における売上成績(円)の分布が図 3のようになっているとしましょう。横軸は売上成績、縦軸は各売上成績を出した営業担当者の人数です。売上成績の平均は同じであることが、ここでのポイントです。
ある営業担当者が商品A, Bで70万円売り上げた場合、ともに平均より+20万円分の売上成績となります。ところが、ここで注意すべきは、ばらつきの情報です。
商品Aの成績分布は広がりがあり、70万円は一定水準以上の営業担当者ならば普通に達成可能な成績に見えます。他方、商品Bの分布はほぼ全ての営業担当者が50万円で、70万円は非常に難しい売上成績です。
すると、同じ70万円分の売上成績であったとしても、データのばらつきを考慮すると、商品Bでこの成績を出すのは難しく、Bの評価は高くするべきだとわかります。データのばらつきを踏まえることで、同じ指標でも意味が変わることを、この例は示しています。
したがって、ある指標の得点の差の大きさを評価するためには、そのデータのばらつきも考慮しなければならないのです。
差の効果量の数式では、得点の差の大きさを標準偏差(データのばらつきの代表的な指標)で割り算することで対処しています[4]。この割り算によって、指標ごとに異なる得点のばらつきを一律化し、同じ基準で得点差の大きさを評価できるようにしているのです。
先ほどの売上成績の例について、架空データで差の効果量を出してみましょう(図 4)。商品A, Bの平均売上成績はどちらも50万円であり、商品Aの標準偏差は20万円、商品Bの標準偏差は10万円としています。
図 4
2つの商品A, Bの売上成績70万円における効果量(架空例)
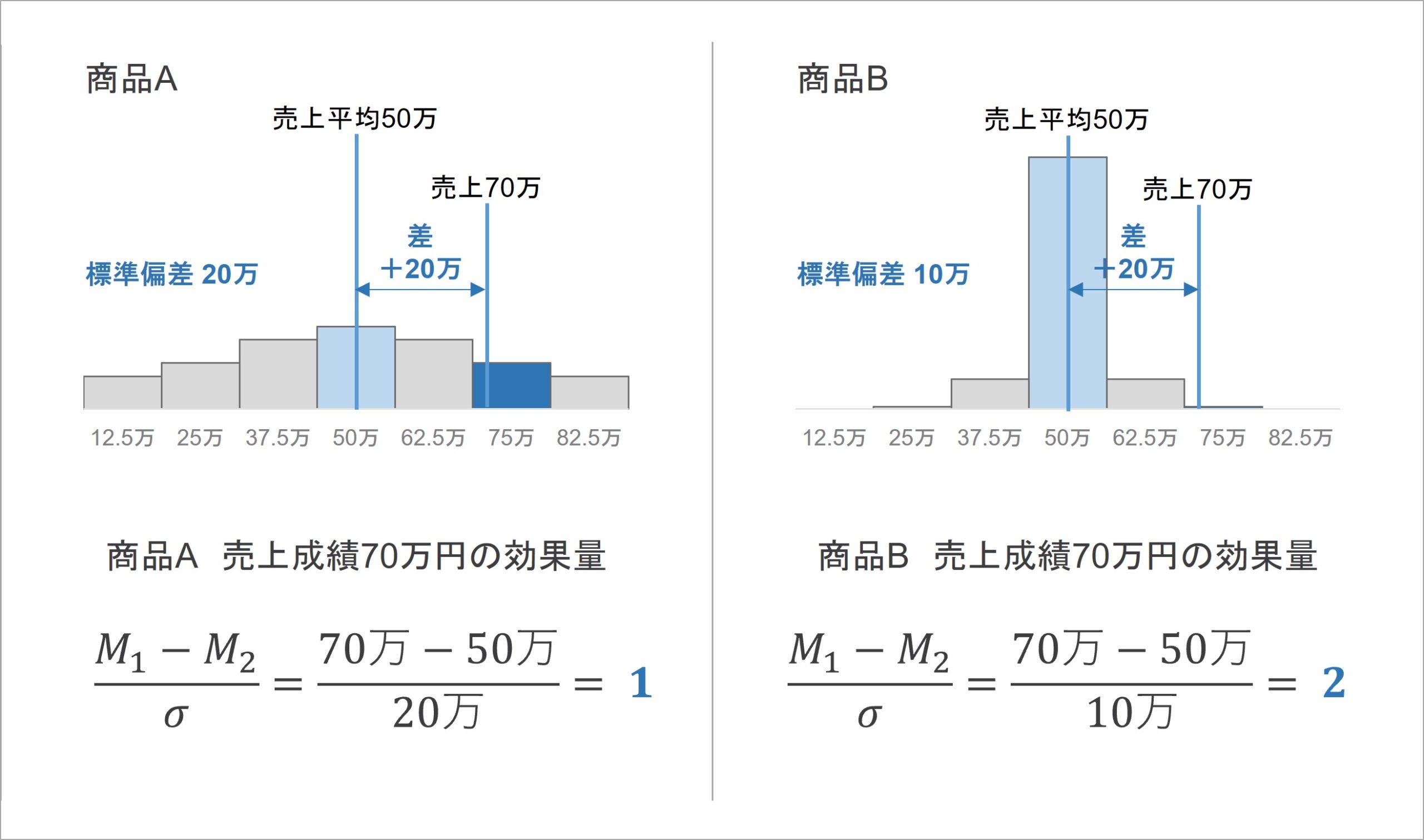
2つの商品について、ある営業担当者の売上成績は70万円としていました。そのため、各商品の売上成績の平均50万円を基準として、差は70万円-50万円=+20万円分となります。
商品Aの効果量を計算すると、商品Aの売上成績の標準偏差(データのばらつき)は20万円でした。そのため、70万円分の売上成績の効果量は、+20万÷20万=1となります。効果量で評価した場合、商品Aにおける70万円分の売上成績は、効果量d = 1ポイント分になるという意味です。
一方、商品Bの効果量を計算すると、商品Bの売上成績の標準偏差は2万円でした。そのため、70万円分の売上成績の効果量は、+20万÷10万=2となります。効果量で評価した場合、商材Aにおける70万円分の売上成績は、効果量d = 2ポイント分になるという意味です。
この計算結果から、商品Bの方が商品Aよりも効果量が大きい、つまり平均50万円に対して、より高い売上成績を出していると見なせます。したがって、商品Bの売上成績はより高く評価した方がよいと判断できるわけです。
このように、データのばらつきを加味した計算をする効果量を駆使することで、ある得点の差の大きさを評価できるようになります。
様々な効果量d
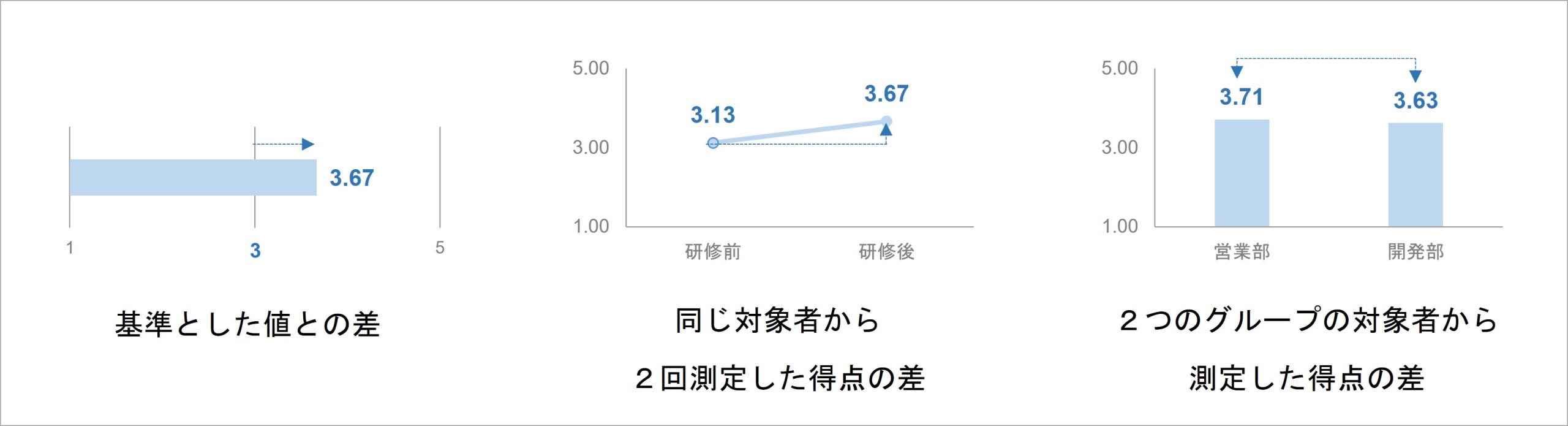
効果量dには、様々な種類があります。2グループ間の得点に差があるか統計的に検証するt検定と同様に、差の捉え方には3つの枠組みがあるためです(図 5)。
「基準とした値との差」は、ある指標の得点や量について、基準とした値との差を見る枠組みです。
先ほどの例「全営業担当者の売上成績の平均に対する、ある営業担当者の売上成績の大きさの検証」は、この枠組みに該当します。分析に際して、ある指標に定めた目標値や基準値と、組織サーベイで示された実際の値を比較するため、それらの差を評価する形です。
「同じ対象者から2回測定した得点の差」は、ある指標の得点や量について、同じ対象者から2回測定したデータの得点差を見る枠組みです。
例えば、学習意欲を向上させる研修に対して行う「研修前後で、学習意欲が上がった程度の検証」が、この枠組みに該当します。学習意欲が上がった程度を、研修前の学習意欲得点と研修後の学習意欲得点の差で評価する形です。
「2つのグループの対象者から測定した得点の差」は、ある指標の得点や量について、2つの異なるグループで測定したデータの得点差を見る枠組みです。
例えば、「営業部と開発部で、学習意欲の程度が異なるかの検証」が、この枠組みに該当します。学習意欲が異なる程度を、営業部の学習意欲得点と開発部の学習意欲得点の差で評価する形です。
3種の差の捉え方に対して、2つの効果量dの数式があります。
図 6
3種の差の捉え方に対する効果量 d の数式(Lakens, 2013, 大久保・岡田, 2012)[5]
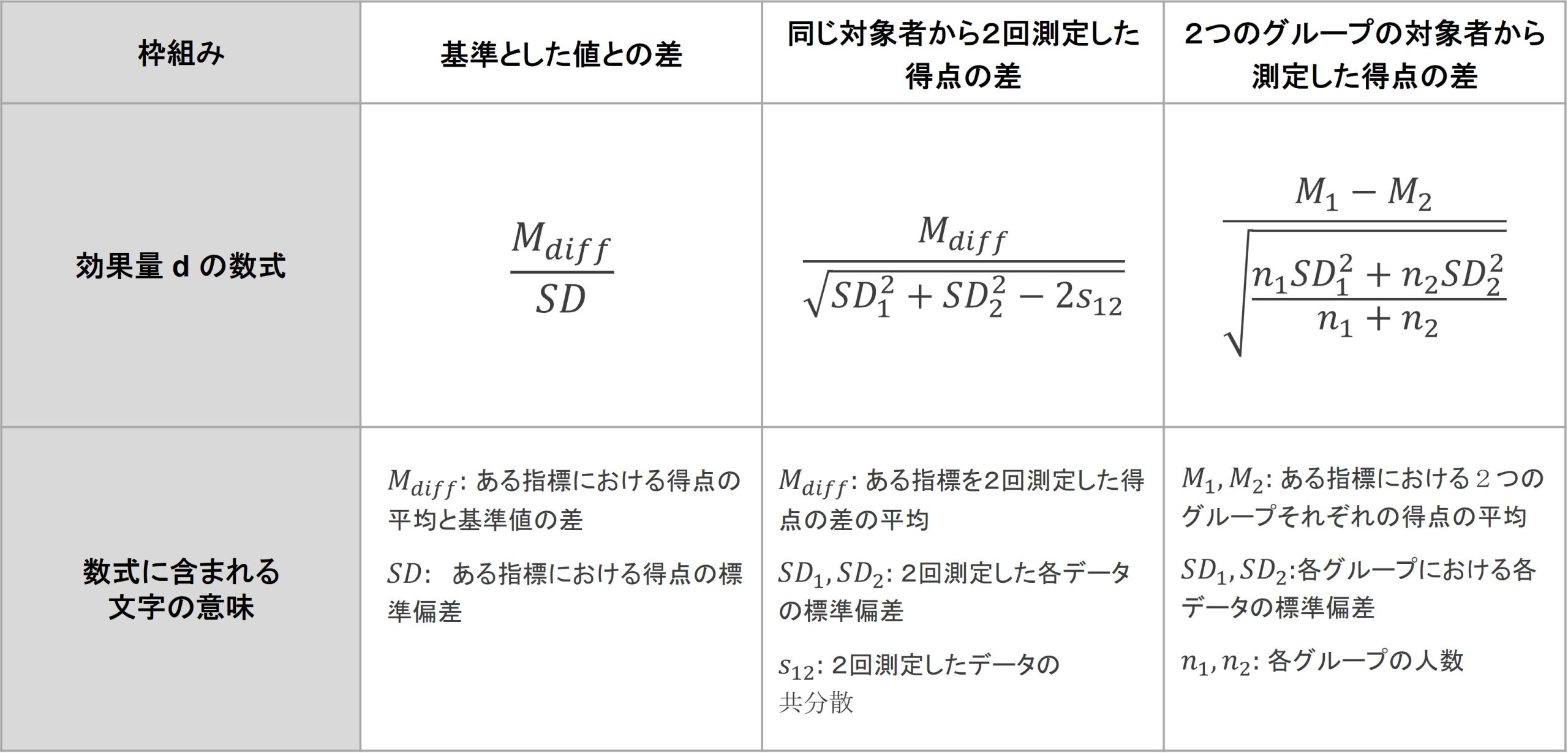
効果量dの数式はいずれも複雑に見えますが、すべて「得点の差をデータのばらつきで割り算する」構造は一貫しています。計算式は違いますが、それぞれの指標は「2つの得点の間に、どの程度差があるのか」を表すものになっています。
d族効果量の値が表す「差の大きさ」の程度
上記の手続きを経てd族効果量が算出できるわけですが、示された値はどのように理解すればよいのでしょうか。この効果量を提唱したCohenは、理解の仕方として2つの方法を示しています(Cohen, 1988)。
ひとつは、効果量dの値に対応する2グループの得点分布が重ならない割合です[6]。具体的には、効果量dは「ある指標の得点において、一方のグループがもう一方のグループの平均得点以上の得点を取る割合」と対応します[7]。そのイメージを、図 7を見ながら捉えていきましょう。
図 7
効果量d(得点差)の大小と一方のグループが他方の平均以上となる割合のイメージ
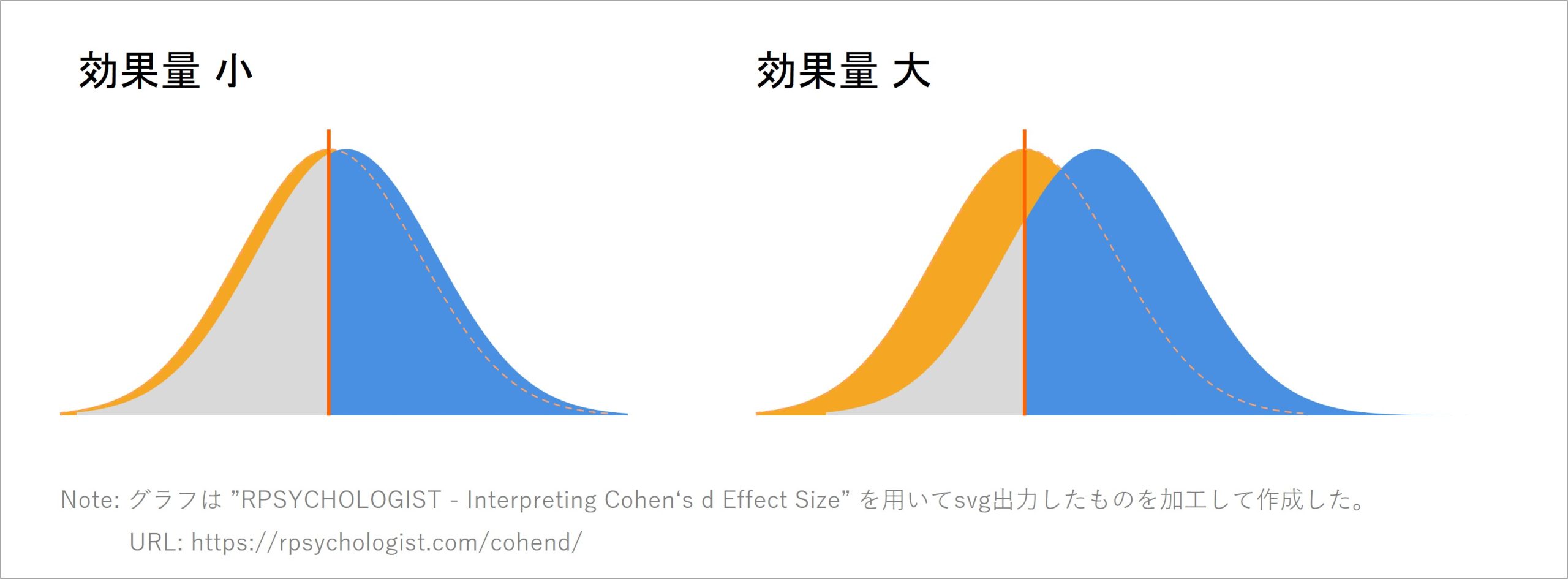
図 7は、橙色の部分が「得点が低いグループの得点分布」、橙色の線が「得点が低いグループにおける平均値」を表します。また、青色の部分は「得点が高いグループの中で、他方のグループの平均を超えている箇所」、灰色の部分が「得点が高いグループの中で、他方のグループの平均を下回っている箇所」になります。青色と灰色を合わせたものが、得点が高いグループ全体の得点分布です。
効果量が小さい、つまりある指標における2つのグループ間で平均得点がほとんど同じときは、各グループにおける得点の分布が近い箇所に存在します。
結果として、得点が高い方の得点分布が、もう一方の得点分布の平均以上の値となるグラフ青色の割合は、ほぼ50%のままとなっています。得点が高いグループでも、40%強は他方のグループを下回る状態です。
逆に、効果量が大きい、つまり平均得点が2つのグループ間で大きく異なるときは、2つの分布が互いに離れていることになります。それにより、得点が高い方の得点分布が、もう一方の得点分布の平均以上の値を取るグラフ青色の割合が大きくなっています。
この青色部分の割合がとりうる範囲は、2グループの得点分布が完全に一致するd = .00のときに最小の50%となります。2グループ間に得点差がないとき、一方のグループが他方のグループの平均を超える得点となる確率は50%だということです。
また、効果量dが大きくなると、2つの得点分布がどんどん離れていくことになります。その結果、得点が高いグループのほぼすべてが、もう一方のグループの平均を超える得点となるため、一方のグループが他方のグループの平均を超える得点となる確率は最大のほぼ100%になります。
まとめると、効果量の大きさは「得点が高いグループが、もう一方のグループの平均を超える得点をとる割合」と対応し、その割合は50%~100%の範囲になるというわけです。
以上のように、2グループ間の得点差の大きさと、2グループの得点分布が重ならない割合は対応しています。Cohen(1988)では、効果量dの大きさに対応した「得点が高い方のグループが、もう一方の平均を超える割合」がまとめられています(表 1)。
表 1
効果量dの大きさと2グループの得点分布が重ならない割合
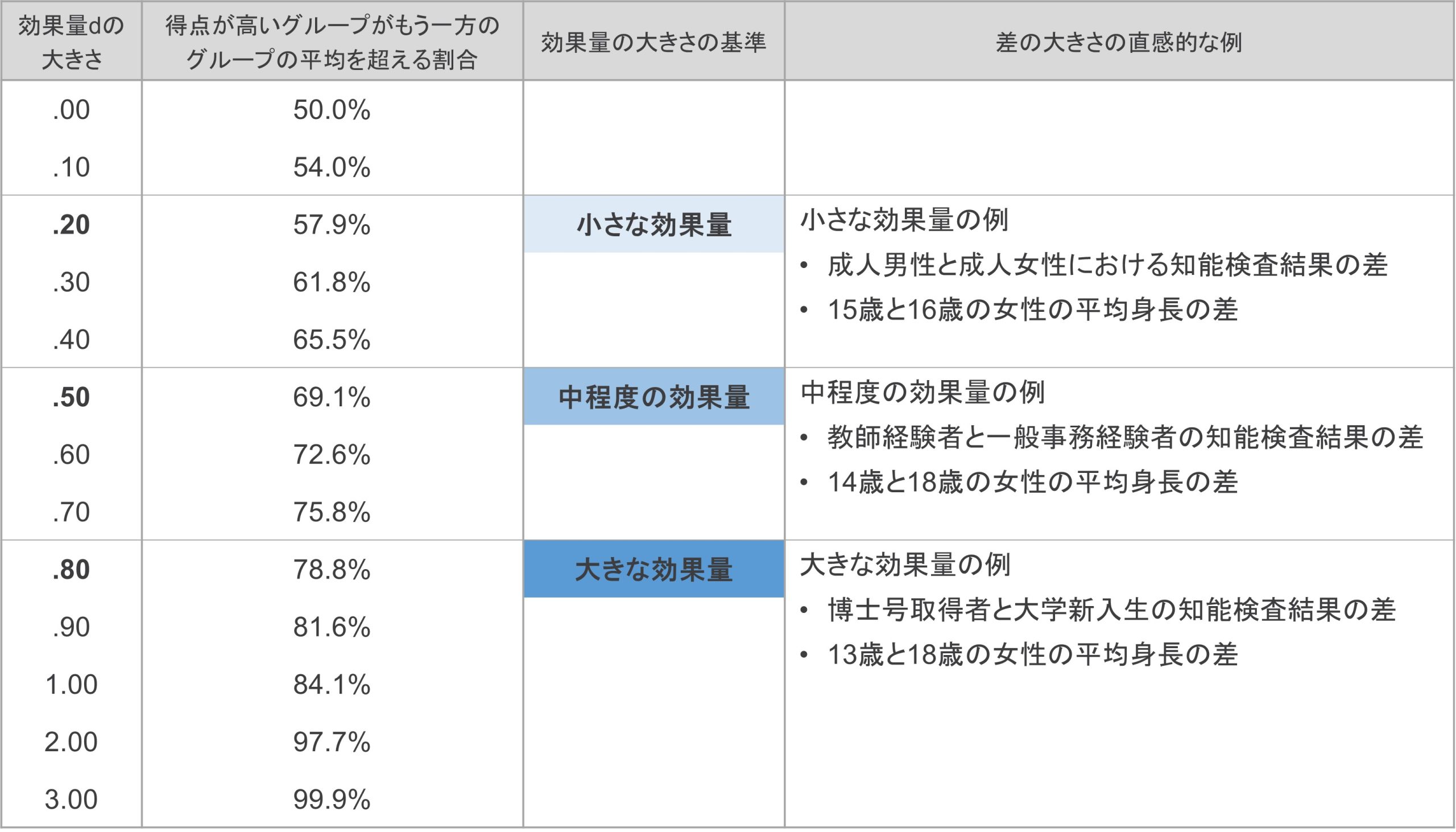
もうひとつの理解の仕方として、効果量dの大きさの基準となる値が設定されています。それは、表 1で示した効果量の値のうち、太字で示されているd = .20, .50, .80です。これらはそれぞれ、効果量小・中・大と見なされる基準値として、設定されています。
加えて、これらの基準値に関して、Cohen(1988)は直感的な例も述べています。表 1の例がその内容です[8]。
例えば、d = .20程度の小さい効果量は、成人男性と成人女性における知能検査結果の差程度の違いとされています。確かに、知能検査の内容によって男女の平均に多少の違いはありそうですが、得意不得意の個人差で簡単に覆るような差とも言えそうです。小さい効果量が表す差の大きさは、そのくらいの感覚の差だということです。
対して、d = .80といった大きな効果量は、博士号取得者と大学新入生における、知能検査の平均的な得点差と同程度の違いだと述べられています。博士号を取得できるほど優秀な人物と一般的な大学新入生では、知能検査の得点が大差となることは想像に難くないでしょう。大きな効果量の感覚は、そのくらいの差だということです。
以上のように、得点の高いグループがもう一方の平均を超えている割合、効果量dの大小を定めた基準値、そして直感的なイメージなどの情報に基づいて、算出された効果量dが示す差の大きさの程度を把握できるのです。
効果量dの注意点
ここでは、効果量dを扱う上での注意点を2つ取り上げます。いずれも、差の大きさを適切に理解する上で重要な論点です。
注意点1.効果量dの大きさは、実質的な得点の大きさと対応していない場合がある
効果量dは、2つの得点の差をデータのばらつきで割り算することで得られる指標です。効果量dが大きくなるのは、得点差が大きいか、データのばらつきが小さいか、いずれかの場合です。そのため、得点の差が小さい指標でも、データのばらつきが非常に小さい場合、効果量dは大きくなります。
例えば、上司部下関係の良さを「1:まったくあてはまらない~5:とてもあてはまる」で測定したデータがあるとします。その回答値平均の目標を3点(どちらともいえない)と定め、これを超えるような回答データが得られたか効果量を算出して確認したら、d = 1.00と大きな値になったとします。
効果量だけで解釈すれば「目標値との差が大きい」と考えられ、「目標を大きく超えた得点となった」と見なせます。しかし、仮に回答値平均が3.3点、標準偏差が0.3だったとすればどうでしょうか。
目標値3点に対して効果量は1.00と大きな値ですが、回答値の平均は3.3点と、そこまで高い値には見えません。ほとんどの人が3.3点周辺の得点に収まっていることから、標準偏差が0.3と非常に小さくなっており、結果として効果量が大きく算出された形です。
データのばらつきが非常に小さい指標は、ほとんどの人が平均付近に集中している状態であることから、その得点がわずかでも基準値を上回る状態に至ることはなかなか難しいと考えられます。しかし、そうはいっても、ほぼ「どちらともいえない」といえるような得点である3.3点を「高い得点だ」と言いにくいでしょう。
このように、効果量が大きいといっても、それが現実においても実質的に大きな得点差であるとは限らないという問題があります。
逆に、小さな効果量が重要な意味を持つ場合も考えられます。例えば、職場のハラスメントが問題視される状況において、ハラスメントを取り上げた研修を行い、研修前後でハラスメント意識度が高まったかを検証したとします。
その結果、研修前後でのハラスメント意識度は、効果量d = .31程度の差で増えていたことが示されたとしましょう。この効果量の大きさは小~中程度であり、研修後のハラスメント意識度の得点分布が発生前の平均を超える割合は61.8%だとわかります。
効果量の程度で見たら、ハラスメント意識度の上昇はそこまで大きくないかもしれませんが、この意識の向上は喫緊の課題であり、研修によってハラスメント意識度が多少は上がっていることは事実です。その意味では、小さいながらも前進が見られたこの結果は、一歩目としては十分と解釈できます。
また、Cohen(1988)は、新たな領域における初めての実践・検証では、その計画・設計やデータ測定に慣れていないため、小さな効果量の結果が出がちだ(p. 25)と擁護しています。研修の方法やデータ測定を練り切れていない初期段階では、小さな効果量に終わる結果が示されるのも無理はないとも考えられます。
これらを踏まえると、効果量が小さいといっても、現実場面において無意味な得点差であると断じるのは早急だと言えるのです。
これらの問題に対処するには、「組織サーベイを設計した時点で、各指標の得点がどの程度ならば高い/低いと見なすか、事前に決めておく」ことが有効です。各指標の得点の大きさに関する評価基準を、事前に定めておくということです。
統計解析の技法に注目が集まる昨今ですが、それに頼り切らず、測定した各指標の得点の意味を、測定・分析した人が責任をもって考え尽くして定義することは、これまで通り重要だといえるでしょう。
注意点2.正確な値を得るには、大きなサンプルサイズが必要
効果量dは、母集団に対する推定値であり、推定には誤差が含まれます。その誤差をできる限り小さくするためには、他の解析手法と同様に、できるだけ大きなサンプルサイズが欲しいところです。
サンプルサイズが小さいと推定精度が低くなり、算出した効果量の大きさが正確でない可能性も高くなります。実際に、数十名のデータで効果量dを算出すると、得点が高めな回答者が集まったためか、非常に大きな効果量の値が得られることもたびたび見られます。
効果量については、他の統計解析手法のように何名いれば十分といったさじ加減はありません。しかし、検証を厳密に行いたいならば、できるだけサンプルサイズを大きくする、つまり多くの回答者に協力してもらい、回答を増やすことが必要になってきます。
以上、本コラムでは効果量、特にd族効果量の中でも効果量dについて解説しました。「統計的に有意」では追いきれないデータの特徴を検証する手法として、ぜひ押さえておきたい解析手続きです。
引用文献
Cohen, J. (1962). The statistical power of abnormal-social psychological research: a review. The Journal of Abnormal and Social Psychology, 65(3), 145-153. https://doi.org/10.1037/h0045186
Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Routledge. https://doi.org/10.4324/9780203771587
Ellis, P. D. (2010). The essential guide to effect sizes: Statistical power, meta-analysis, and the interpretation of research results. Cambridge university press. https://doi.org/10.1017/CBO9780511761676
Kirk, R. E. (2005). Effect size measures. In B. S. Everitt & D. C. Howell (Eds.), Encyclopedia of Statistics in Behavioral Science (Vol. 2, pp. 532-542). Springer.
Lakens, D. (2013). Calculating and reporting effect sizes to facilitate cumulative science: a practical primer for t-tests and ANOVAs. Frontiers in psychology, 4, 863. https://doi.org/10.3389/fpsyg.2013.00863
大久保 街亜・岡田 謙介 (2012). 伝えるための心理統計 効果量・信頼区間・検定力 勁草書房
Rosenthal, R. (1994). Parametric measures of effect size. In H. Cooper, & L. Hedges (Eds.), The handbook of research synthesis (pp. 231-244). Russell Sage Foundation.
脚注
[1] 本コラムをお読みいただく前に、セミナーレポート「人事のためのデータ分析入門『統計的に有意』とは何か」や「人事のためのデータ分析講座「統計的に有意」を学ぶ」をご覧いただくことをお勧めします。
[2] 帰無仮説検定におけるこの性質は、この手法の問題点というより、それを用いる人間側が勘違いしやすいポイントとして理解するべきでしょう。散布図や相関係数の値そのものを確認すれば、統計的に有意である相関だと認められたとしても、「指標間に実質的な対応関係はなさそうだ」と判断できます。しかし、そういった判断を省略し「統計的に有意な相関である」という言葉のインパクトのみ捉えてしまうと、「2つの指標間に、十分に強い相関関係があった」と勘違いしてしまいます。その意味で、この統計学的性質は問題点と呼ぶべきものではなく、人間側の理解の仕方の問題なのです。
[3] Kirk(2005)では、実に70種以上の効果量指標が挙げられており、差や関連の大きさをどう捉えるのか、その多様性が表れています。
[4] 差の効果量の数式におけるデータのばらつき(標準偏差)は、「母集団におけるデータのばらつき」の推定値となっており、一般に記述統計で算出される(標本の)標準偏差とは異なるものになっています。
[5] Cohenが提唱した効果量dは、データのばらつき(母集団の標準偏差)の計算において偏り(バイアス)が生じる問題があるとされています。それに対処するように、データのばらつきの計算法を修正した差の効果量の指標も提案されています。この点は、大久保・岡田(2012)で詳しく解説されています。
[6] 厳密には、ここでは「2つのグループが同じサンプルサイズであり、母集団分布が正規分布であり、母集団の分散が等しい」ことが仮定されています。
[7] Cohen(1988)は、2グループの得点分布が重ならない割合を、ここで紹介したものを含めて3種類提案しています。ここで紹介したものはU3と呼ばれる割合です。このほかに、「2グループの得点分布が重なっていない割合」を直接計算したU1、「2グループの平均の中間値をとり、あるグループが中間値以上の得点を取る割合」を計算したU2があります。詳しくは、大久保・岡田(2012)で解説されています。
[8] ここに挙がる身長差の例について、Cohenはアメリカの統計学者であったことを踏まえると、アメリカの女性のデータについて述べたものだと考えられます。そのため、身長の例は、日本の女性における身長差の感覚と少し違っているかもしれません。
執筆者
株式会社ビジネスリサーチラボ フェロー。信州大学人文学部卒業,信州大学大学院人文科学研究科修士課程修了。修士(文学)。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を、他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており、通常では捉えることが困難な、様々なデータの背後にある特徴や関係性を分析・可視化し、その実態を把握する支援を行っている。