ビジネスリサーチラボは、2023年2月にセミナー「人事のためのデータ分析講座　「統計的に有意」を学ぶ」を開催しました。人事DXが進む中、データ分析を活かした意思決定が重視されています。データ分析を活用するには、根底にある統計学的な考え方を知ることが不可欠です。本セミナーでは、ビジネスリサーチラボ・フェローの能渡真澄から、データ分析を活用する上で重要な知識である「統計的に有意」について、解説しました。

※レポートはセミナーの内容を基に編集・再構成したものです。

登壇者

能渡真澄

株式会社ビジネスリサーチラボ フェロー。信州大学人文学部卒業，信州大学大学院人文科学研究科修士課程修了。修士（文学）。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を、他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており、通常では捉えることが困難な、様々なデータの背後にある特徴や関係性を分析・可視化し、その実態を把握する支援を行っている。

1. 「統計的に有意」とは何か

近年、デジタルトランスフォーメーションが進む中で、データの利活用が増えてきています。様々なIT機器を活用してデータを測定し、そのデータを活かしてエビデンスに基づく意思決定を行うことが推奨されるようになってきました。

測定されたデータを元に意思決定することで、意思決定の根拠がよりはっきりして、その後の評価も行いやすくなります。データを測定・分析しやすくなった現代において、これらの実践はますます重視されることになるでしょう。

さて、そうはいっても、「データを測定したけれど、どう活用すれば良いのだろう」と悩む方は数多くいます。

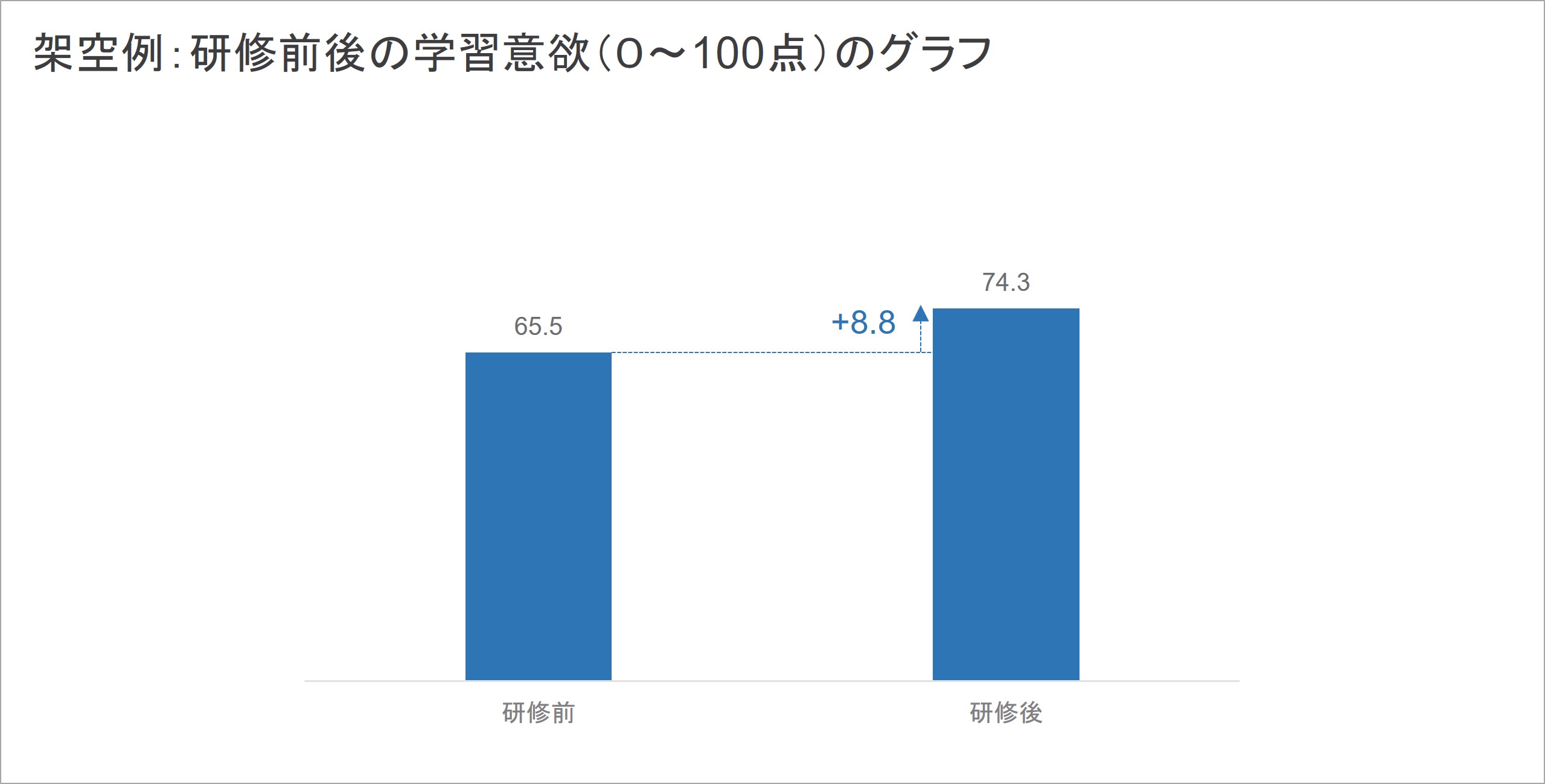
例えば、職場における学習の促進を狙った研修を実施したとしましょう。ここでは、その効果検証として、「研修の前後で測定した研修受講者たちの学習意欲」を比較しました。研修前後に、学習意欲を0～100点で評価するサーベイを実施し、20名の受講者から回答を集めた架空データを集計した結果が以下のものになります。

このような形で、測定したデータを集計したところ、研修前後で学習意欲の得点が8.8ポイント上昇していることが示されました。この結果から「研修後に学習意欲が上がった」ことは、一応示すことができたわけです。

このグラフを元に、上司や経営層に研修成果を説明していくわけですが、ここで悩んでしまうかもしれません。例えば、「この集計結果を見せて得点が上がっていたことを示すだけで十分なのか」「この結果で、この研修に学習意欲上昇の効果があるといって良いのか」など、心配は尽きません。

悩みが出てくる理由のひとつは、この集計結果が、今回のサーベイで得たデータで偶然出ただけのものである可能性があるからです。

「このデータは、今回のサーベイに回答してくれた人だけで示された結果であり、今後も同じような結果になるとは限らない」「そういった偏りを考慮してみると、この程度の得点上昇で効果ありと言える根拠は何なのか」ということです。

このような悩みを解消するエビデンスのひとつを提供できるのが、「統計的に有意」となります。

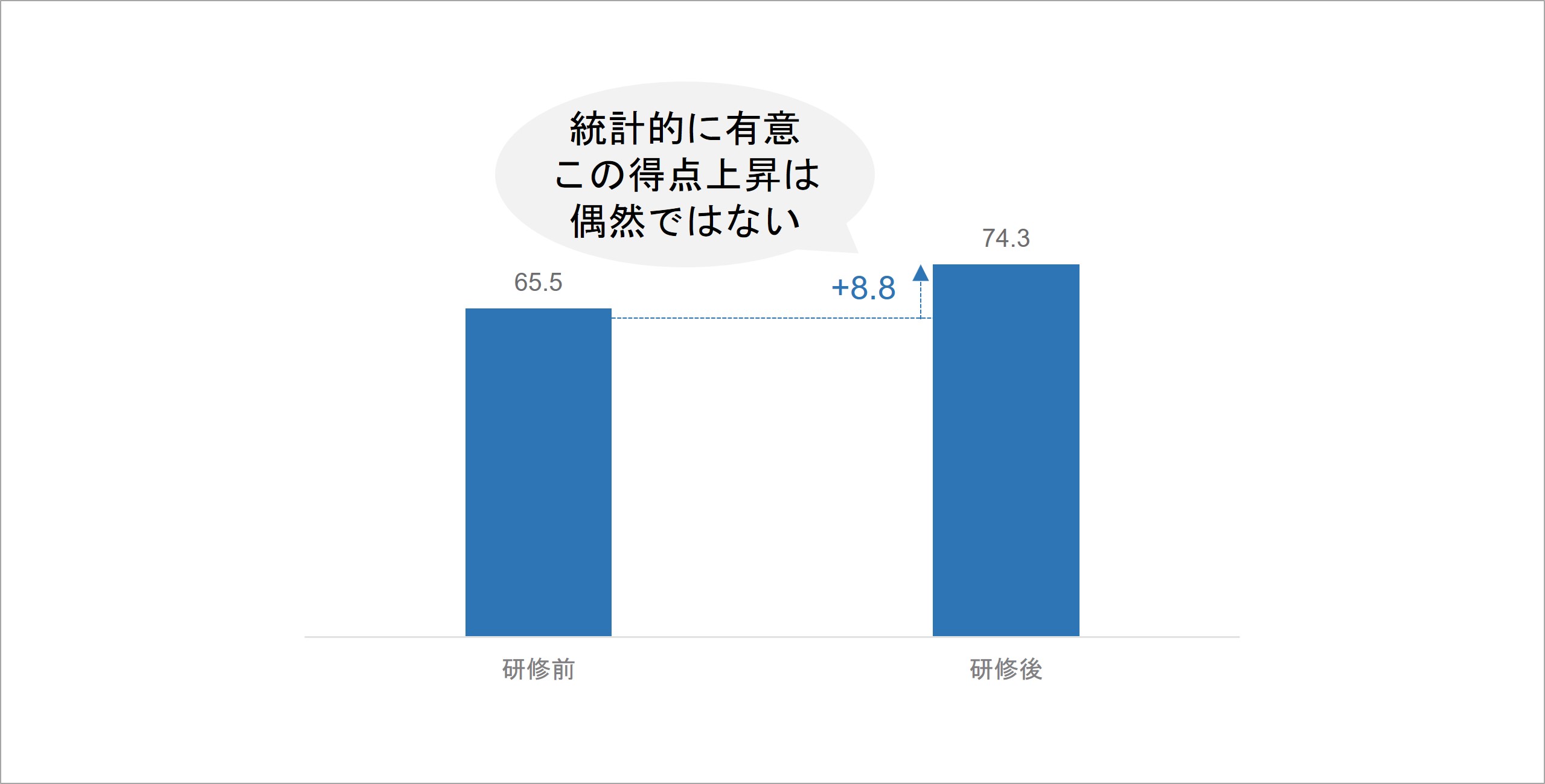
「統計的に有意」とは、分析結果が、ランダムな要因や偶然によって説明されないことを指します。このサーベイで示された分析結果が、今回得られたデータで偶然示されたものでないということです。

例えば、先ほどのグラフでは、研修前後における学習意欲の得点上昇が統計的に有意か否か、検証できます。この検証で「学習意欲の得点上昇が、統計的に有意である」と示すことができれば、研修前後の得点上昇は今回のデータで偶然得られた結果ではないと主張できるようになります。

これによって、「今後も同様の研修を実施すれば、学習意欲の上昇が見込める」といえるエビデンスのひとつが得られるのです[1]。

ここで示した例は研修前後の得点差ですが、その他の関心ごとについても同じようなことが可能です。

例えば、「営業部と開発部で、組織コミットメントが違うか」といったグループ間の差の比較や、「上司部下関係とワークエンゲージメントには関連があるのか」といった指標間の関連の有無についても、統計的に有意か検証することができます。

それらの分析により、手元のデータで示されたグループ間の差や指標間の関連についても、今回のデータで偶然示された結果ではないと主張できるようになるのです。

このように、統計的に有意かという検証を活かせば、測定したデータから述べられることを拡大できます。ここからは、「統計的に有意」の意味をさらに掘り下げるべく、記述統計・推測統計と呼ばれる2つの枠組みについて解説していきます。

2. 記述統計：手元のデータの特徴を示す

記述統計とは何か

記述統計とは、サーベイで得られた回答データそのものの特徴を表すための分析手続きです。サーベイで実際に取得できたデータにアプローチする分析となります。

記述統計の具体例は、一般的に行われているデータ集計です。各指標の平均を算出したり、割合を示したりするデータ集計は、サーベイで得られたデータ、すなわち「標本」における特徴を示す手続きであり、記述統計の典型的な方法となります。

この他に、サーベイで得られたデータにおいて、2指標間の得点がどの程度対応しているかを数値化する相関係数も、記述統計のひとつです。

ここで、統計学的な観点で、記述統計がどういった事柄にアプローチしているかを見ていきましょう。多くの方々が実施しているデータ集計といった記述統計は、統計学的にどういった意味を持っているのでしょうか。

まず、サーベイで得られるデータは、本来データを取りたい全対象者のうち一部の対象者の回答データとなります。

例えば、先ほどの学習意欲を高める研修については、研修に参加した人としていない人が存在するかもしれません。対象者全員に参加してほしい研修だとしても、実際には参加していない、あるいは参加できない対象者は存在しており、当然ながらその人からのデータはとれません。

加えて、サーベイで得られるデータは、その参加者のうち、サーベイに回答してくれた受講者の回答データに限られます。サーベイに参加はしたけれども、何かの理由でサーベイに回答しなかった受講者は、やはり回答データがありません。

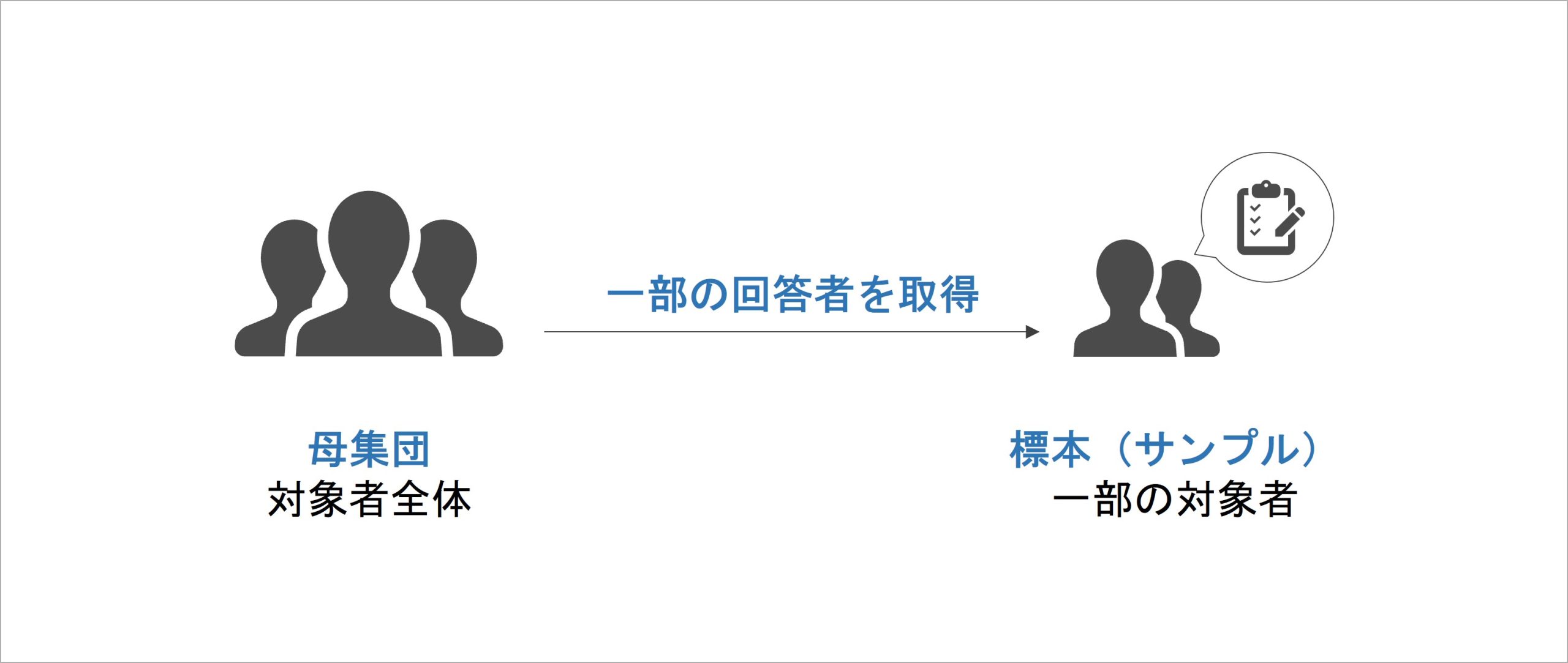
以上を踏まえると、サーベイで得られたデータは、データを取りたい対象者全体に対して、一部の対象者の回答データとなります。

統計学では、これらを2つに分けて捉える考え方を持っています。前者の「データを取りたい対象者全体」を母集団、後者の「サーベイで得られた一部の対象者の回答データ」を標本（あるいはサンプル）と呼びます。

記述統計は、これら2つのうち標本（サンプル）の特徴を見るものになります。実際に手元に得られた一部の回答データに対するアプローチであると、明確に線引きされているのです。逆に言えば、記述統計は、母集団における特徴の表現については一切触れていないこともわかります。

記述統計のメリットとデメリット

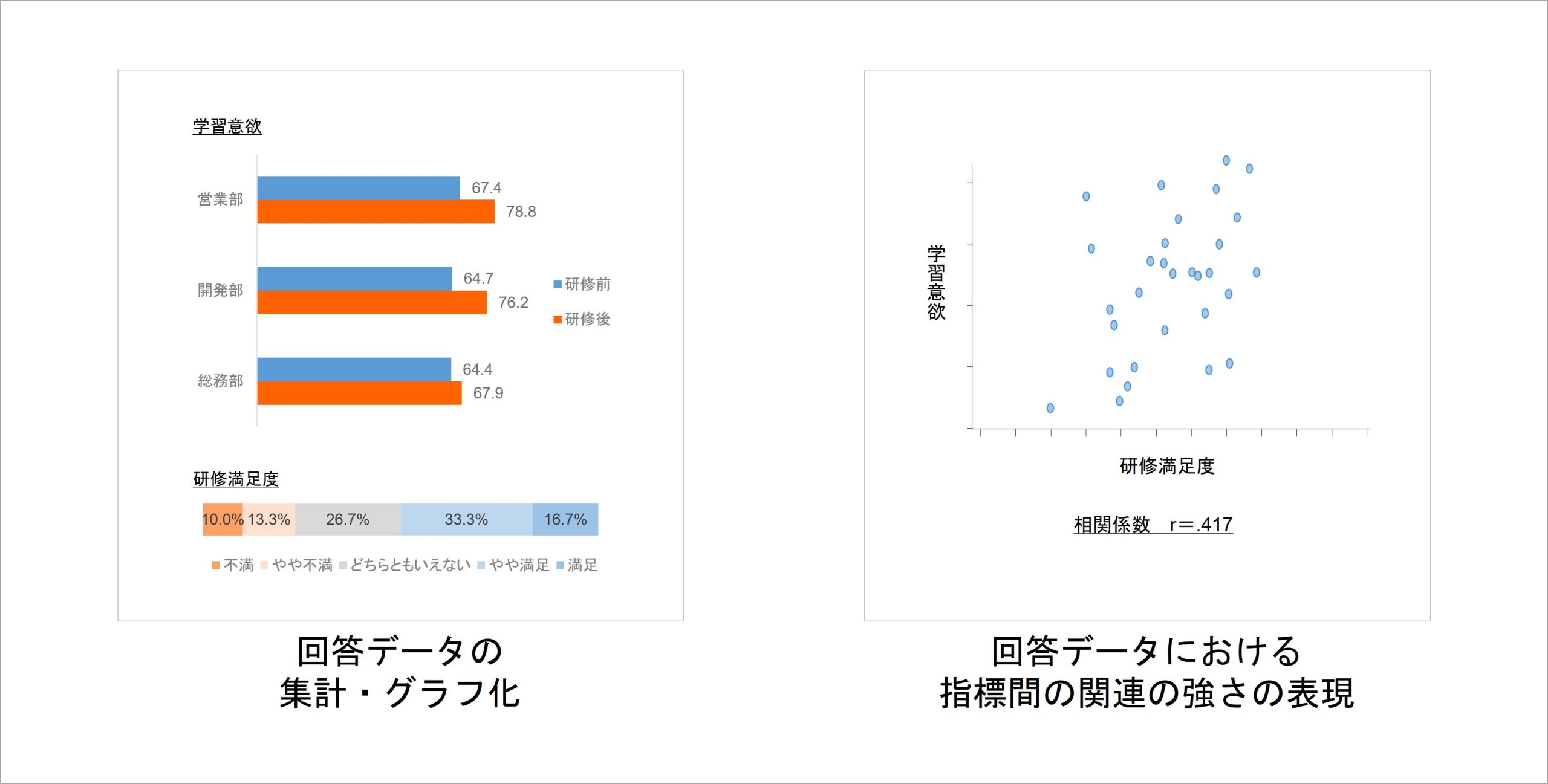
記述統計のメリットは、サーベイで得られたデータが持つ特徴を、詳細に示すことができる点です。

上の図のように、今回得られたデータにおける平均や各選択肢の選択割合はどうだったか、2指標間の関連はどうなっていたかなど、サーベイが捉えた現状・実態をそのまま把握することに適しています。

他方、記述統計のデメリットは、サーベイにてもっとも検討したい事柄である「対象者全体（母集団）の特徴」の予測には使いにくいことです。

記述統計が示す結果は、あくまでサーベイで取得されたデータ、すなわち標本の特徴です。そのため、記述統計には、最初の例で示した「集計結果が、今回のサーベイで得られたデータで偶然出ただけのものである可能性」の問題が、そのまま残っているのです。

仮に、記述統計で示された結果がそのサーベイで偶然得られたにすぎないデータならば、データが得られていない対象者全体について、記述統計の結果から話を広げて考えるのは不適切です。記述統計は、その結果をデータが得られていない対象者全体にあてはめて考えても良いのか、わからないのがデメリットです。

3. 推測統計：データのない対象者全体を推測する

推測統計とは何か

「集計結果が、今回のサーベイで得られたデータで偶然出ただけのものである可能性がある」という問題に対して役立つのが、推測統計です。

推測統計とは、サーベイで得られた一部の対象者の回答データから、対象者全体の特徴を推測する分析手続きのことです。一部の対象者の回答データである標本に着目した手続きが記述統計でしたが、推測統計は、対象者全体である母集団にアプローチする手続きとなります。

推測統計を用いた検証をすれば、サーベイで得られた一部の対象者のデータから、本来検討したい対象者全体の特徴を推測し、全体の特徴に関して主張がしやすくなるのです。

今回解説する「統計的に有意」の検証も、推測統計の一種となります。以降では、統計的に有意の検証に焦点を当てて、解説を進めていきます。

4. 帰無仮説検定：「統計的に有意」の検証

最初に触れたとおり、「統計的に有意」とは、サーベイで得られたある指標の得点差や指標間の関連が、偶然に示されたものでないことを表しています。ここからは、その検証手続きである「帰無仮説検定」について紹介していきます。

帰無仮説検定とは、検証したい事柄を対象者全体における仮説[2]としてまとめた上で、それを否定する仮説（帰無仮説）を検証する分析手続きを指します。対象者全体、つまり母集団に関する仮説を否定するような帰無仮説を設定することがポイントです。

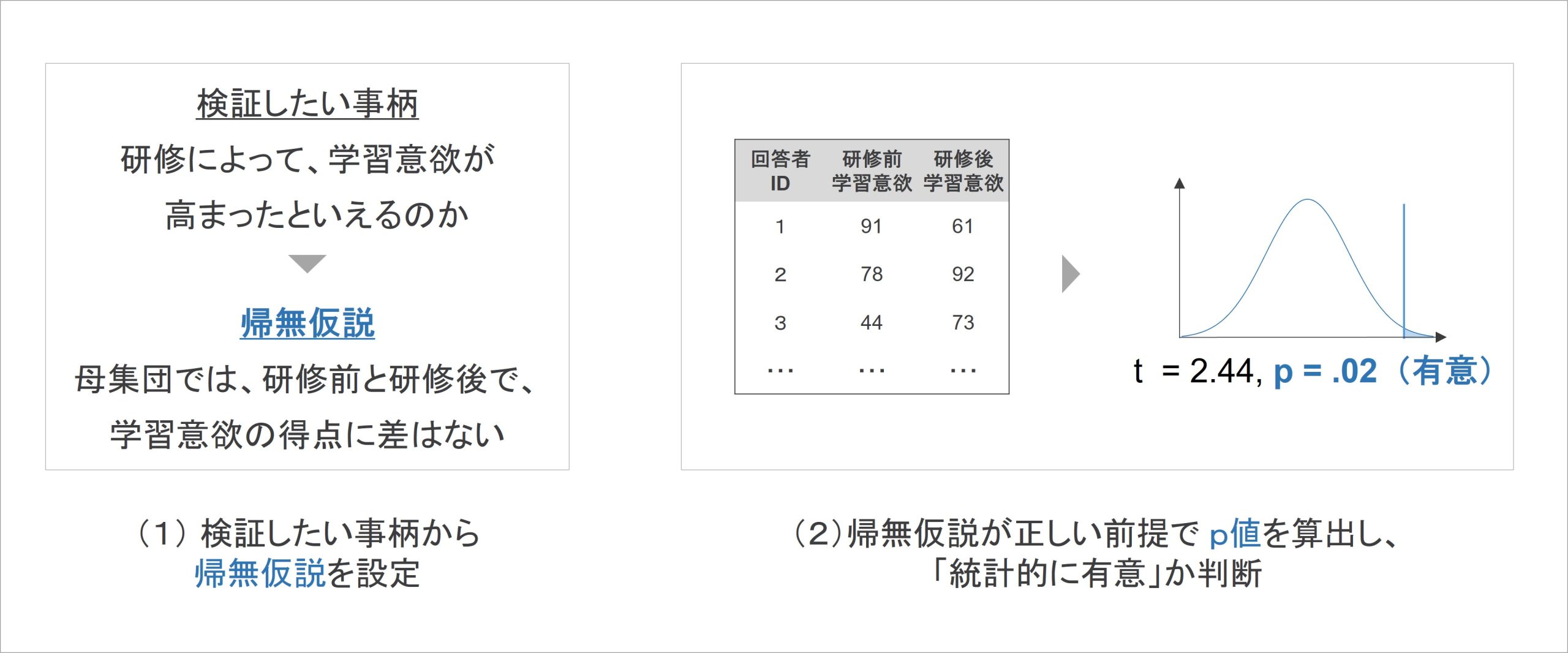
帰無仮説検定は、おおまかに2つのステップから構成されています。

帰無仮説検定では、最初に、検証したい事柄に対応した帰無仮説を設定します。その後、帰無仮説が正しい前提において、p値と呼ばれる指標を算出し、p値の小ささから「統計的に有意」か判断していきます。

（1）帰無仮説の設定

帰無仮説検定で最初に行うことは、帰無仮説を設定することです。検証したい事柄に対して、それがデータにおいてどのような結果として示されるか、対象者全体を取り上げた仮説を立てていきます。

例えば、「学習意欲を高める研修には、効果があったのか」を検証したい事柄とします。これがデータにおいて結果に示されるとすれば、研修前よりも研修後で、学習意欲の得点は高くなっている状態だと考えられます。

これを対象者全体、つまり母集団における仮説としてまとめるので、仮説としては「母集団では、研修前よりも研修後の方が、学習意欲の得点は高い」となります。

次に、これを否定する仮説である帰無仮説を設定します。特に、帰無仮説では「差がない」「違いがない」「関連がない」など、元の仮説で言及した差や関連について、それらが「ない」ことを指すようにまとめるのがポイントです。

先の例でいえば、元の仮説は「母集団では、研修前よりも研修後の方が、学習意欲の得点は高い」でした。すると、帰無仮説は「母集団では、研修前と研修後で、学習意欲の得点に差はない」となります。

帰無仮説に至る仮説構築の流れをまとめると、以下のようになります。

検証したい事柄：「学習意欲を高める研修には、効果があったのか」
元の仮説：「母集団では、研修前よりも研修後の方が、学習意欲の得点は高い」
帰無仮説：「母集団では、研修前と研修後で、学習意欲の得点に差はない」

（2）p値の算出と「統計的に有意」の判断

次に、（1）で設定した帰無仮説に基づいて、p値と呼ばれる指標を算出します。

p値とは、検証に用いる指標（検定統計量）の値が、サーベイで得られた回答データを超える値となるデータを今後のサーベイで得られる確率のことです。誤りを含めつつも、理解しやすさを最優先して言い換えると「今回のサーベイで得られた結果となるようなデータが、今後のサーベイで得られる確率」がｐ値となります。

p値の算出で最大のポイントは、帰無仮説が正しいことが確率計算の前提となっていることです。帰無仮説は「差がない」「関連がない」といった内容の仮説となりますが、これが正しい前提で、p値は計算されます。

例えば、研修による学習意欲の向上効果を検証するとしましょう。そのときのp値は、帰無仮説「母集団では、研修前と研修後で、学習意欲の得点に差はない」が正しい、という前提のもとで、今回のサーベイで得られたデータを超えるような結果が今後のサーベイで得られる確率を計算します。

最初に挙げた例のグラフでは、研修前の学習意欲が65.5点、研修後の学習意欲が74.3点であり、研修前後で8.8ポイント分の得点上昇が見られていました。この得点差に得点ののび方の個人差も加味した上で、得点上昇の大きさ（検定統計量）を計算し、それを超えるようなデータを今後得られる確率を算出するわけです[3]。

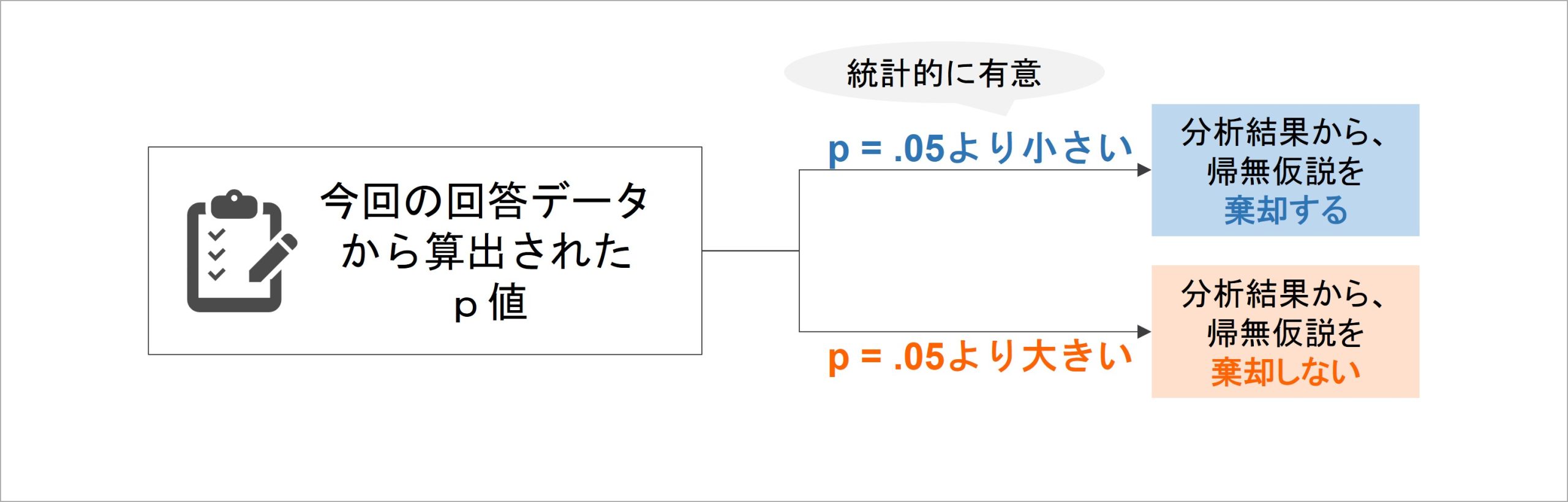
このような手続きを経てp値を算出したら、その値の小ささを元に、帰無仮説が棄却できるか判断します。経営学や心理学では、慣習的にp値がp = .05（5%）を下回ったら、帰無仮説を棄却する判断を下します[4]。

ここで、p値が5%を下回る値となったら「統計的に有意」であると見なします。学習意欲の研修効果の例で言えば、仮にサーベイで得られた学習意欲の得点上昇量に関するp値がp = .024だったとしたら、これはp = .05を下回る値なため、「研修前後における学習意欲の得点上昇は、統計的に有意」と判断されます。

ここで、p値が5％より低いなら帰無仮説が棄却できる理由について説明を加えます。単純なイメージなら「今回のサーベイと似たようなデータが今後得られる確率が高い方が良いのでは」と思うかもしれません。しかし、p値の計算には、論理的に帰無仮説を棄却するためのロジックが存在します。

今回のサーベイで得られたデータにおける結果（検定統計量）を超えるようなデータが新たに得られる確率がp値でしたが、その確率計算は「帰無仮説が正しい前提」で行われていました。

この状況下で小さなp値が算出されることは、「帰無仮説が正しい前提の元で、今回のサーベイで得られたデータの結果を超えるようなデータを得られる確率は、非常に小さい」ことを意味します。帰無仮説を前提とすると、今回のサーベイで示される結果になるようなデータを得ることは、非常にまれだということです。

それほどに確率が低いp値が得られたとしたら、何かがおかしなことになっていると考えるわけですが、帰無仮説検定では「確率計算の土台にある帰無仮説が誤っているから、これほど低確率なp値となるのだ」と見なします。

今回のデータを踏まえると、前提としていた帰無仮説「差がない」「関連はない」はおかしいと見なすわけです。

このような判断プロセスを用いるため、p値の小ささが、帰無仮説を誤りと見なすか・棄却できるか判断する指標として機能するのです。

p値による帰無仮説の棄却判断ができたら、母集団に関する推測をまとめていきます。

検証の結果、帰無仮説が棄却されたなら「差がない」「関連がない」という仮説が誤りだと判断されたことになるため、「差がある」「関連がある」と結論されることになります。そこから、元の仮説が支持されると主張できるわけです。

ここまでの例で言えば、帰無仮説は「母集団では、研修前と研修後で、学習意欲の得点に差はない」でした。この帰無仮説が棄却され、誤りだと判断されると、そこから得られる結論は「母集団では、研修前と研修後で、学習意欲の得点に差がある」となります。

なお、この時点では、研修前後で得点に差があるといえるだけで、研修前と後でどちらの得点が高いかは決まりません。

そこで、最初の例のグラフを見ると、研修後に得点が上昇していました。このことから、対象者全体における研修前後の得点差は、研修後の方で得点が高い意味での得点差であると.判断されます。

他方、もしも帰無仮説が棄却されなかったら、支持できる仮説が存在しないことになります[5]。支持できる仮説がないため、「今回のデータからは、母集団の特徴について言及できない」と、判断は保留されることになります。

以上のプロセスを経て、帰無仮説が棄却されると、元の仮説「母集団では、研修前よりも研修後の方が、学習意欲の得点は高い」が支持されることになります。

このようにして「統計的に有意」は、帰無仮説の設定から、p値による帰無仮説の棄却判断を経て、対象者全体の特徴を推測することができます。

その結果、サーベイで得られた一部のデータから、対象者全体の特徴に関するエビデンスが得られ、データ解析を元にした主張ができるようになるのです。

5. 「統計的に有意」の注意点

ここからは、「統計的に有意」な結果の解釈について、注意点を3つ挙げます。示された分析結果の解釈を広げすぎないようにするためのポイントです。

「統計的に有意である」≠差が大きい、関連が強い

よくある勘違いのひとつであり、注意が必要なポイントです。

例えば、研修前後の得点差について統計的に有意な結果が示された際、そこから「研修前後で、得点に”大きな差”があったのだ」と勘違いして解釈するケースがたびたび見られます。

「統計的に有意」の検証は先ほど見てきた通り、帰無仮説を棄却できるかで判断をしています。そして、帰無仮説はたいていの場合、「差は0である」「関連は0である」など、何かしらの値がない状態であることを述べたものになります。

そのような帰無仮説を棄却することで主張できるのは、「差は0ではない」「関連は0ではない」ことまでです。差や関連が「0ではない」と言っているだけであり、差や関連がどの程度の大きさ・強さなのかについては、ここから言及できないのです。

したがって、「統計的に有意」であると示されても、その結果をもとに「差が大きい」「関連が強い」と主張するのは、誤りとなります[6]。

具体的な差の大きさや関連の強さについても主張したい場合は、ひとまず記述統計で示された差の大きさ・関連の強さの指標を参照するとよいでしょう[7]。例えば、研修前後の学習意欲の上昇に関しては、サーベイで得られたデータで示された研修前後の得点差を参照することが可能です。

回答者が偏ると、推測も偏る

こちらは、推測統計の限界として意識すべき、注意点となります。サーベイへの回答者に偏りがあると、そのデータから推測される対象者全体の特徴も、もちろん偏ります。

例えば、従業員全体の組織エンゲージメントを高める要因を探るサーベイを実施した結果、権限の委譲が有効だと示されたとしましょう。しかし、そのサーベイに回答したのが、入社5年以上の中堅層からベテラン社員がほとんどだとしたらどうでしょうか。

サーベイで得られたデータが入社5年以上の中堅層からベテラン社員でほとんど構成されているならば、そのデータから推測される対象者全体も中堅層からベテラン社員全体となります。すると、その推測が新入社員や若手社員にあてはまる結果なのか、わかりません。

帰無仮説検定（統計的に有意）を含む推測統計全体の弱点として、手元に得られたデータから推測する性質上、手元のデータの回答者に偏りがある場合、その推測も偏る点は考慮すべきです。

そのため、検証したい事柄に応じた対象者全体を想定できたら、その対象者層をしっかり狙って、サーベイの回答がもらえるよう広くアプローチすることが重要です。

そして、実際にサーベイで得られたデータの記述統計を見て回答者の特徴を把握し、推測統計で検証される対象者全体がどのあたりの従業員層になっているか考えるよう心がけましょう。

6. さいごに：「統計的に有意」から学べること

このセミナーでは、「統計的に有意」とは何かについて解説しました。統計的に有意か検証することで、サーベイで得られたデータから、データが得られていない全体の特徴を推測できるようになる点は、非常に魅力的でしょう。

その一方で、サーベイで得られたデータを詳細に表す記述統計も、非常に大事な手続きです。帰無仮説検定に慣れて、統計的に有意か検証できるようになると、記述統計をおろそかにしがちになることがよくありますが、記述統計の確認も重要な実践です。

記述統計は、そのサーベイで得られたデータの特徴を詳しく示す意味で、現状や実態の把握を詳細にできる点が魅力です。また、「統計的に有意」は、注意点で述べたとおり、様々な限界があります。

データの得られていない対象者全体の推測ができるようになる帰無仮説検定は魅力的ですが、得られたデータを丁寧に見通して現状を把握する記述統計は有用なのです。統計的に有意のことを知ったからこそ、ぜひ記述統計で現状を丁寧に追うことも意識したいところです。

加えて、このセミナーで紹介したように、統計学ではデータが取れていない対象者全体（母集団）と、サーベイに回答した一部の対象者（標本）を分けて考える枠組みを持っています。この観点は、皆さんがぜひこれからデータを扱う際に意識していただきたい枠組みです。

サーベイの集計値からすぐに対象者全体の推測をしないよう注意する意味でも、サーベイの集計にてひとまず示された結果と、データが取れていない対象者全体の特徴は、異なる可能性があることは、常に意識したいところです。

サーベイデータの単純集計に加えて、帰無仮説検定による「統計的に有意」かの判断を行い、データに基づいた検証をより深めていきましょう。

Q & A

Q. 少ないサンプルサイズにおける帰無仮説検定で統計的に有意な結果が得られた場合、堂々と有意な結果だと主張してよいか。

私の考えでは、有意な結果だと主張して問題ないと思います。

サンプルサイズが小さいデータは、統計的に有意だと示されにくい性質があります。全体の回答者数が少ない分、平均的な傾向から外れる回答者が少しでもいると、それに引っ張られる形で推測が大きくぶれやすいためです。そのような状況下で得られた有意な結果であるため、堂々と主張して良いと考えられます。

ただし、注意点で述べた通り、「統計的に有意」は具体的な差の大きさや関連の強さは言及していません。サンプルサイズが小さいと、その後のサーベイにおいて、最初のサーベイで示された差の大きさや関連の強さとは異なる値が示される可能性が高い点は、考慮しておくべきでしょう。

Q. 統計ツールで計算した際、p値がp = 0と完全に0になった。分析に誤りがあるのだろうか。

おそらく、正しい結果です。私の知る限り、統計ツールでp値を算出した際に明らかにおかしな値となるならば、何かしらのエラーが出るはずです。それが出ていないなら正しい値と考えられます。

その結果は、例えばp = .0000001などｐ値が非常に小さい値なため、ツールが値を表示しきれなかった結果としてp = .00と出力したと考えられます。そして、そのような非常に小さいp値は、得点の差や関連の強さが非常に大きいか、サンプルサイズが大きいデータでは度々見られるものです。

以上を踏まえると、p = .00の出力は「帰無仮説を前提とした際に、今回のサーベイで得られたデータを超えるようなものを今後得られる確率は、ほぼ0％」と考えられ、通常の手続き通り5%を下回ったp値として処理していけばよい、となります。

---

脚注

[1] ここで「エビデンスのひとつが得られる」と書いたとおり、厳密に言えば、この検証だけで「この研修に効果があった」とは主張できません。統計的に有意であることが表すのは「研修後の得点上昇は偶然でない」ということであり、得点上昇の理由が研修参加以外の何かである可能性を否定できないからです。この論点は、「ある要因による影響の有無」の検証方法について議論する「実験計画法」で扱われる枠組みです。

[2] なお、統計学ではこの仮説を「対立仮説」と呼びます。帰無仮説に対立する形で構成される仮説としてこの呼び名がついていますが、検証したい事柄に対応する仮説である点を強調してわかりやすくするため、この解説では検証仮説と呼んでいます。

[3] p値を算出するための指標である検定統計量は、分析ごとに様々な種類があります。今回のセミナーは帰無仮説検定全体の流れの解説が目的なため、検定統計量とそれに基づくp値の具体的な計算方法については、今後のセミナーで紹介していきます。

[4] この基準となる確率は有意水準と呼ばれ、研究領域ごとに様々な基準値が設定されています。

[5] 高校数学の「集合と論理」にて、ある命題が正しい（真）か誤り（偽）かは、「反例がひとつでもあると偽、反例が一切ないと証明できたら真」で判断していたことを覚えているでしょうか。帰無仮説が棄却されない状況は、帰無仮説が正しいとするデータが一つ得られただけであり、「反例が一切ない」ことを表しません。結果として、これは帰無仮説が正しいと支持することにならず、支持できる仮説が存在しない保留状態に至ります。なお、帰無仮説が棄却される状況では、p値の判断によって帰無仮説が誤っている反例を一つ示しています。そのため、帰無仮説を偽として「差がある」「関連がある」と結論づけられるわけです。

[6] 統計学的な特徴を補足すると、帰無仮説検定は、サンプルサイズが大きい（分析に用いる回答データの件数が多い）ほど、「統計的に有意である」と示されやすい性質があります。得点差の大きさや関連の強さ以外の理由で統計的に有意か否かの判断が左右されるわけですから、「統計的に有意」だと示されても、それは「得点差が大きいこと」や「関連性が強いこと」を意味しないことになるわけです。

[7]また、データを取りたい対象者全体（母集団）における差の大きさや関連の強さをより詳しく検証する方法として、「効果量」と呼ばれる指標や「信頼区間」と呼ばれる範囲を算出して検討する手段もあります。