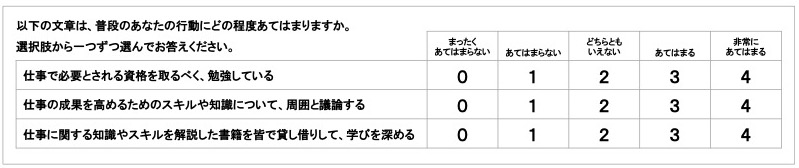
組織サーベイにおいては、アンケートに対する従業員の回答に対して、決められた方法で数値を割り振ります。例えば、従業員がスキル開発を進めようとする意欲（以下、スキル開発意欲）を測定することを目的に、従業員に以下の質問への回答を求めたとします。

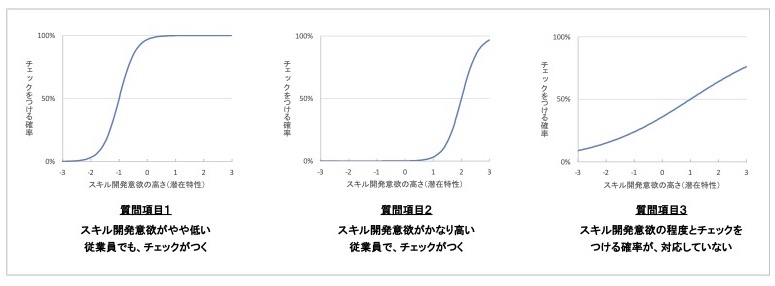
図 1　「スキル開発意欲」を測定する質問項目

これらの質問に対して、「各項目をチェックした個数を、スキル開発意欲の得点とする」と定めたとしましょう。すると、すべてにチェックを入れていない０点から、すべてにチェックを入れた３点で、０～３点の得点幅となります。

このような方法で測定すれば、従業員のスキル開発意欲の程度を捉える得点が算出できます。得点が高いほど、スキルを開発する意欲が高いとみなすわけです。

しかし、この得点化方法には議論すべき問題があります。それは「各質問にチェックをつけるために求められるスキル開発意欲の高さが、質問によって大きく異なる」ことです。 

例に挙げた質問のうち、「仕事で必要とされる資格を取るべく、勉強する」は、仕事に必要な資格である以上、よほどスキル開発意欲が低い従業員でない限り、まず実践すると考えられます。

すると、この質問はスキル開発意欲が非常に低い人でない限り、チェックするでしょう。最低限のスキル開発意欲がある従業員なら、この質問にはチェックがつくということです。

それと比べて、「仕事の成果を高めるためのスキルや知識について、周囲と議論する」ことは、スキル開発意欲がかなり高くないと実践しないでしょう。仕事に有用なスキルや知識について周囲と議論することは、スキルを高めようとする強い意欲がないとできないと思われます。

つまり、「仕事の成果を高めるためのスキルや知識について、周囲と議論する」という質問は、スキル開発意欲が非常に高い従業員でない限り、チェックがつかないのです。 

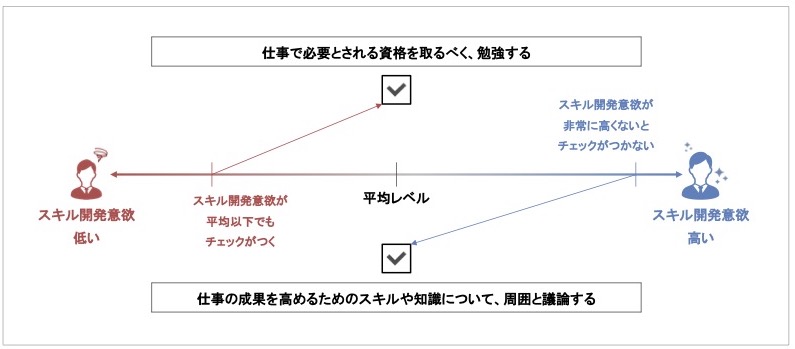
以上をふまえると、これらのスキル開発意欲に関する２つの質問は、その質問にチェックをつけるか否かにおいて、図 2のように異なるレベルのスキル開発意欲が想定されていると考えられます。

図 2　各質問へのチェックに想定される、スキル開発意欲の程度

ある従業員のスキル開発意欲の高さが、矢印の開始地点のレベルを越えたとき、その従業員が矢印の先の質問項目にチェックをつけるというイメージです。

図2における上の質問は、平均以下のスキル開発意欲を持つ従業員でもチェックをつけますが、下の質問はスキル開発意欲が相当に高くないと、なかなかチェックがつかないと考えられます。

このように、各質問にチェックをつける行為に想定されるスキル開発意欲の高さは、質問ごとに異なっています。しかし、これらの質問項目における得点化の方法は「各項目をチェックした個数を、スキル開発意欲の得点とする」であり、その違いをうまく捉えられていません。

この問題は、質問内容について０～４の選択肢から回答を選ぶ形式でも生じます。先ほどのチェックリストの表現を「０：まったくあてはまらない～４：非常にあてはまる」の構成に変えて考えてみましょう。

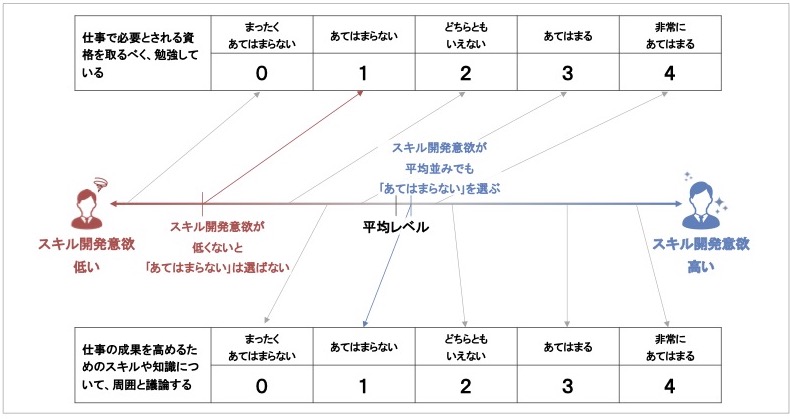
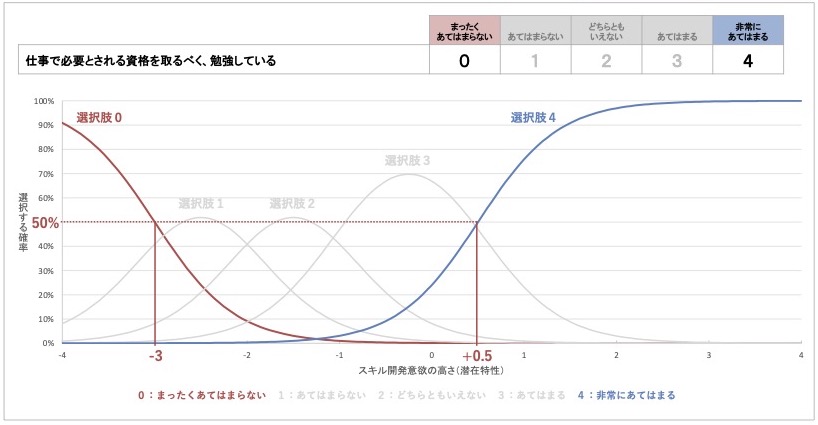
図 3　各質問への５つの選択肢に想定される、スキル開発意欲の程度

回答者のスキル開発意欲の高さが矢印の開始地点周辺のレベルならば、その矢印が指す地点にある選択肢が選ばれるイメージです。

ここでは、『あてはまらない』選択肢に着目してみます。図 3の上にある質問内容では、よほどスキル開発意欲が低い従業員でないと、『あてはまらない』という否定的な選択肢を選ぶことはないでしょう。

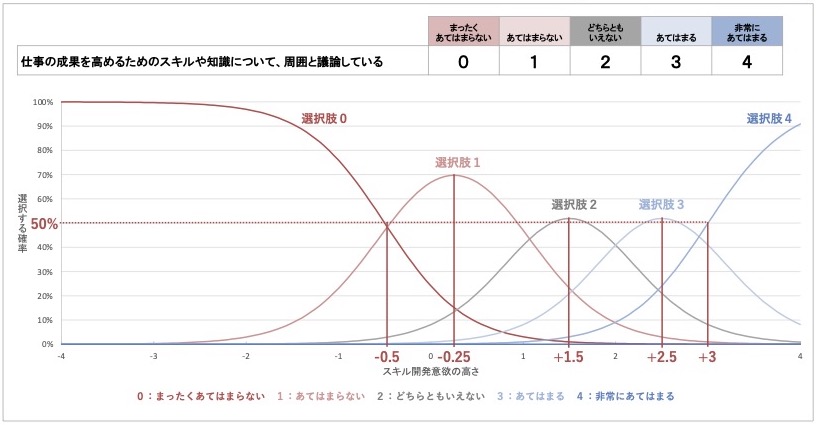
他方、図 3の下にある質問内容では、スキル開発意欲が平均並みな従業員でも『あてはまらない』という否定的な選択肢を選ぶかもしれません。平均程度のスキル開発意欲では、スキル開発のために周囲と議論まで行うことはなかなか難しく、『あてはまらない』と答える可能性が高いと考えられます。

他の選択肢を見ても、上の質問と下の質問の間で、同じ選択肢であってもそれと対応するスキル開発意欲の高さは異なっているのが分かります。

このように、回答を０～４の選択肢方式にしても、各選択肢が反映するスキル開発意欲の程度は、質問項目ごとに異なるのです。この問題をしっかり検証・考慮せずに得点を算出しては、測定したい概念の程度を正確に得点に反映できません。その一方で、組織サーベイにおける得点の算出において、この問題を意識することは実際にはほとんどないでしょう。

しかし、仮にこの問題を抱えたまま各指標を得点化してしまうと、部署間で得点に差異があっても、その得点差が各指標の程度の違いを反映しているのか、厳密にはわかりません。組織の状態を探るサーベイとしては、この点も意識することが望ましいと言えます。

それでは、「組織サーベイの各質問項目の回答から算出した得点の高さは、測定したい概念の程度を適切に反映しているのか」を、どう検証すればよいのでしょうか。本コラムでは、その検証や得点計算を可能とする「項目反応理論」について紹介していきます[1]。

各質問項目の測定性能を詳しく検証する：項目反応理論

項目反応理論とは、項目応答理論とも呼ばれ、各質問項目に対する回答と測定する概念の関係性について、質問項目が持つ特徴と回答者の特徴を分けて解析する統計アプローチを指します。

項目反応理論の大きな特徴は、先ほど挙げた「各質問項目が捉える、測定概念の高低の違いが得点に反映されない」という問題を、数理モデルの中で解消している点です。そこでは、数理モデルを駆使して、各質問項目への回答に想定される概念の高さとその測定精度が表現されます。

まずは、先ほど例に挙げたチェックリストのように、２択で回答を求めるタイプの質問について、項目反応理論による分析を適用した例を見ていきましょう。

なお項目反応理論では、基本的に、複数の質問項目を用いて単一の概念を測定している状態を想定します。最初に示した例でいえば、先述の質問項目３つは「スキル開発意欲」のみを捉えており、他の概念は関係しないことを前提としています。この点は、最後に述べる注意点で詳しく紹介します。

そして、その測定概念と各質問への回答の対応を見るため、統計モデルを用いて「項目特性曲線」（ICC: item characteristic curve）と呼ばれるグラフを描き、各項目の特徴を捉えていきます。

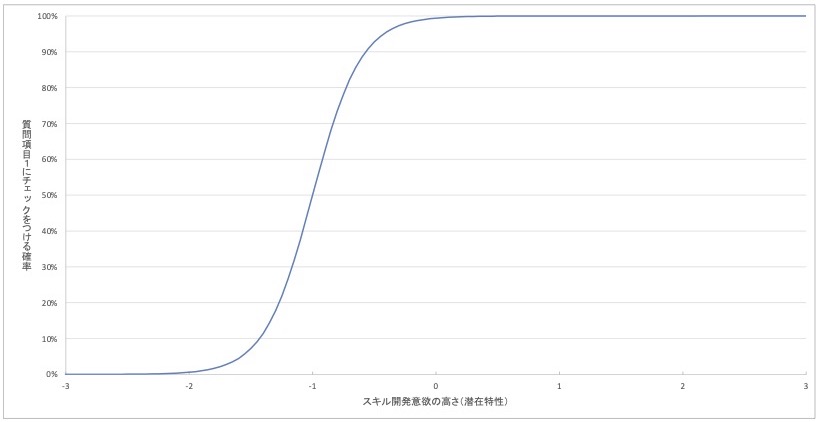
まずは、質問項目１「仕事で必要とされる資格を取るべく、勉強する」の回答をチェックリストで行ったデータから推定される、項目特性曲線を見てみましょう。なお、以降の例で示すグラフは架空例であり、実際のデータで推定されたものではありません。

図 4　質問項目１の項目特性曲線（架空例）

このグラフでは、縦軸に「その問題にチェックをつける確率」を取ります。０％ならばその質問にチェックをつける可能性はなく、100%ならばその質問には確実にチェックをつけると考えられます。もちろん、50％ならばチェックをつける確率は半々であると考えられます。

また、横軸には測定したい概念の程度をとります。今回の例でいえば、従業員のスキル開発意欲の程度です。スキル開発意欲が平均的な従業員を０として、右に行くほど意欲が高いことを表します。

横軸の数値は、項目反応理論では「潜在特性」と呼ばれるもので、測定したい概念の高さを表します。例えば、スキル開発意欲でいえば、潜在特性０点は「平均的なスキル開発意欲を持つ回答者」を表し、＋1点は「上位16％程度のスキル開発意欲を持つ回答者」を表す、という具合です[2]。

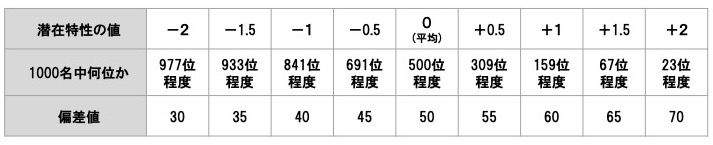
潜在特性がいくつあれば高いといえるかは、測定概念の内容も含めて様々な解釈が考えられます。ここでは、各潜在特性の値が、測定したい概念の高さをどう表すかについて、直感的にわかりやすいものとして、1000名中何位と位置付けられるか計算したものと、それを偏差値に換算した表を示しておきます。

なお、統計学に慣れている人に向けて簡単に記述すると、「潜在特性の高さは、因子得点や標準化得点の大きさと同じような解釈の仕方で良い」となります。

図 5　潜在特性の値と対応する順位、偏差値

項目特性曲線に話を戻します。このグラフの特徴は「ある質問にチェックをつける確率が、測定したい概念を回答者が有する程度に応じて、グラフに図示される」ことです。図 4のグラフを見ると、スキル開発意欲の潜在特性が－1点のとき、グラフが0％から100％に向けて一気に上昇しています。

この結果から、「スキル開発意欲の高さが1000名中841位程度を超えた従業員だと、質問項目１にチェックをつける可能性が高まる」ことが読み取れます。言い換えると、従業員のスキル開発意欲がまあまあ低い程度を超えているならば、この質問にチェックがつけられ始めるということです。

この解釈を質問項目で置き換えると、「従業員のスキル開発意欲が841位程度の高さを超えた従業員のあたりから、『仕事で必要とされる資格を取るべく、勉強する』という項目にチェックをつけるようになる」と考えられます。質問項目１はスキル開発意欲がそこまで高くなくてもチェックがつくことが把握できるわけです。

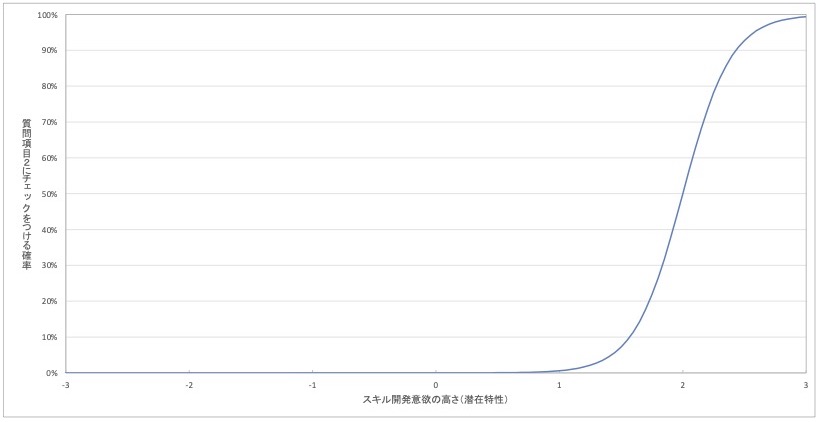
続いて、質問項目２「仕事の成果を高めるためのスキルや知識について、周囲と議論する」の項目特性曲線の例を見てみましょう。

図 6　質問項目２の項目特性曲線（架空例）

先ほどと比べて、こちらのグラフは０%から100％へと確率が高まるタイミングが、より右側に存在しています。具体的には、スキル開発意欲の潜在特性が＋２点で、グラフが0％から100％に向けて上昇しています。

この結果から、「スキル開発意欲が1000名中23位程度の従業員だと、質問項目２にチェックをつける可能性が高まる」ことが読み取れます。この質問にチェックがつけられ始めるのは、スキル開発意欲が上位２％程度の高さを超えた従業員だということです。

この解釈を質問項目で置き換えてみると、「従業員のスキル開発意欲が上位２％の高さを超えた従業員から、『仕事の成果を高めるためのスキルや知識について、周囲と議論する』にチェックが入るようになる」と考えられます。質問項目２は、スキル開発意欲が相当に高くないとチェックが入らないことがうかがえます。

このように、項目特性曲線を用いることで、ある質問にチェックがつくことと、測定したい概念の程度がどう対応するかを検証することができます。「質問項目１と２で、捉えるスキル開発意欲の高さが異なるのでは」という懸念が、項目特性曲線を基に検証できるのです。 

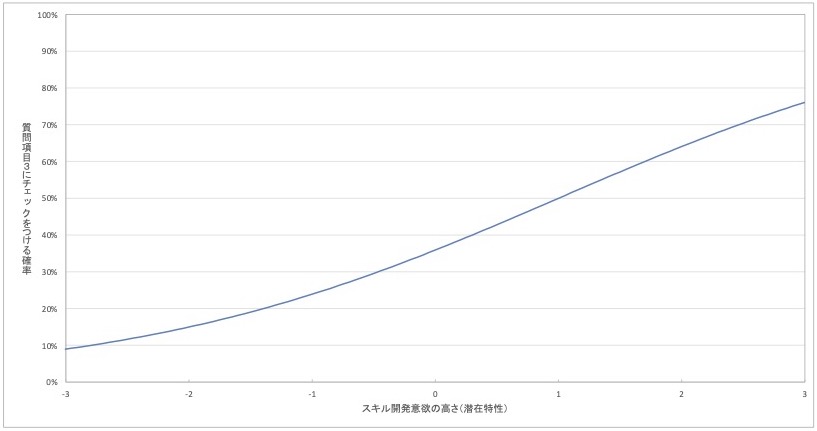
さらに、質問項目３「仕事に関する知識やスキルを解説した書籍を皆で貸し借りして、学びを深める」の項目特性曲線の例を見てみましょう。

図 7　質問項目３の項目特性曲線（架空例）

このグラフは、これまで示した２つのグラフと比べて、確率の上昇が緩やかになっています。チェックがつく確率が50％を超えるのは、スキル開発意欲の潜在特性が＋1点のところですが、それよりスキル開発意欲が高い従業員でも、この質問にチェックをつける確率はなかなか100％にならないのです。 

これは、「質問項目３は、回答者のスキル開発意欲の高低と、この質問にチェックがつくか否かが、はっきり対応していない」ことを意味しています。スキル開発意欲が高い人でもチェックがつかないかもしれませんし、スキル開発意欲が低い人なのにチェックをつけてしまうかもしれません。

上記のグラフは架空例ですが、質問項目３は、「書籍を購入」「皆で貸し借り」といった内容が独特です。それによって、他２項目が捉える単純なスキル開発意欲とは異なる特徴を捉えてしまい、スキル開発意欲の程度とチェックの有無がうまく対応しなかったのかもしれません。

以上を踏まえると、質問項目３は、スキル開発意欲の程度を捉える質問として有用でないとわかります。スキル開発意欲が低い人でもこの質問にチェックをつける可能性がある以上、この質問にチェックがついたとしても、その理由が「スキル開発意欲が高いからだ」と言い切れないのです。

項目特性曲線は、グラフが急になる位置のみならず、その傾き具合についても有意義な情報を提供してくれます。傾きが緩やかなグラフは、測定したい概念の程度とチェックがつく確率が対応しておらず、測定したい概念に対する測定精度が低いというわけです。

このように、項目特性曲線を見ることで、その質問項目への回答に対応した測定したい概念の程度、および測定の精度が把握でき、各質問の特徴をより詳しく知ることができます。

図 8　３つの項目特性曲線と、その解釈の比較

グラフの位置と傾き具合の指標：困難度と識別力

項目特性曲線は、グラフが急になる位置とその傾き具合から各質問の測定性能を検証できますが、グラフを描くためには数式が必要です。

項目特性曲線のグラフを描くための関数式を、項目特性関数（item characteristic function）と言います。本コラムでは、チェックの有無や「はい/いいえ」など２択で回答するタイプの質問によく用いられる、２パラメタ・ロジスティックモデルを紹介します。

図 9　２択質問の項目特性関数（２パラメタ・ロジスティックモデル）

このモデルは、グラフの位置の情報を表す「困難度」と、グラフの傾き具合の情報を表す「識別力」を式に含み、これらによって先ほど示したグラフの違いを表現しています。

ここでは関数の式を示しますが、これを暗記する必要はありません。困難度と識別力の指標がグラフの見た目にどういった違いを生み出すか、そのイメージを理解できれば十分です。

困難度（difficulty）とは、ある質問項目にチェックをつける確率が50％となる点における潜在特性の高さを表す指標です（Hambleton & Swaminathan, 1985）。潜在特性は、先ほどスキル開発意欲の高さを例に説明した「測定したい概念の高さ」を表す指標です。

困難度が高いほど、チェックをつける確率が50％を超えるために必要な潜在特性の値が高いことを表します。つまり、困難度が高い質問項目は、測定したい概念の程度が相応に高くないと、その項目にチェックがつく可能性が高まらないことになります。

困難度によるグラフの違いは、先ほど示した質問項目１と２の違いになります。質問項目１のグラフはチェックをつける確率が急激に高まるポイントが左側にあり、質問項目２のグラフでは右側にありましたが、これは困難度の違いです。 

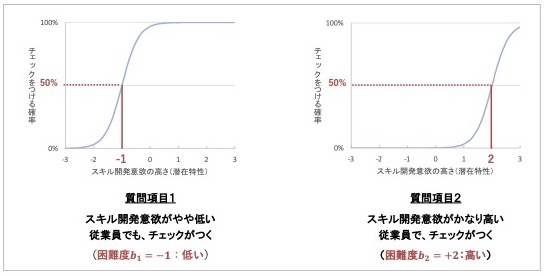
図 10　質問項目１と質問項目２の項目特性曲線と困難度の比較

質問項目１は、スキル開発意欲がやや低い従業員でもチェックをつける確率が高いグラフでした。この項目の困難度、つまりチェックをつける確率が50％となる点のスキル開発意欲の潜在特性は、－１点と低い値です。

一方、質問項目２は、スキル開発意欲がかなり高い従業員でようやくチェックをつける確率が高まるグラフでした。この項目の困難度は、＋２点と高い値となっています。

このように、各質問項目が捉えるスキル開発意欲の程度の違いは、困難度の大きさの違いとして数値化されます。

次に、識別力（discrimination）とは、ある質問項目にチェックをつける確率が50％となる点における、項目特性曲線のグラフの傾きを表す指標です（Hambleton & Swaminathan, 1985）。

識別力が大きいほど、グラフの傾きが急なことを表します。言い換えると、潜在特性の値がある地点を超えると、すぐに確率が0％から100％になることを意味します。つまり、「識別力が高い質問項目では、特定の潜在特性の値を超えたらすぐにチェックがつく確率が0％から100％になる」ことを表します。

それが意味することは、前述の質問項目２と３の比較がわかりやすいでしょう。

図 11　質問項目２と質問項目３の項目特性曲線と識別力の比較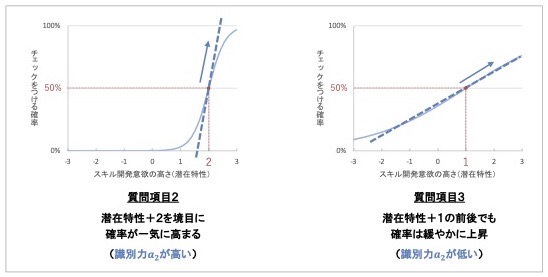

質問項目２は、この質問にチェックをつける確率が50％となる点の前後で、チェックをつける確率が０%から100％に向けて一気に上昇しています。グラフの傾きが急であり、識別力が高い質問項目です。

これは、「質問項目２は、スキル開発意欲が上位２％程度の高さを超えたか否かで、チェックの有無が決まる」と判断できることを表します。つまり、質問項目２は回答者のスキル開発意欲が上位２％程度あるか否かを、うまく識別できる項目だということです。

一方、質問項目３において、この質問にチェックをつける確率が50％となる点は、スキル開発意欲の潜在特性が＋１点のところです。しかし、その点の前後でもグラフの傾きは緩やかであり、０％から100％に向けてじわじわと上昇しています。識別力が低い項目は、グラフがこのような状態になります。

質問項目３では、識別力が低く、スキル開発意欲の潜在特性が＋１点を超えても、その質問にチェックをつける確率が100％にすぐさま近づかず、はっきりしません。

結果として、「回答者のスキル開発意欲が上位16％程度の高さを超えた従業員だとしても、質問項目３にチェックがつくとは限らない」と解釈できます。逆に、スキル開発意欲が上位16%程度の高さを下回っている従業員が、質問項目３にチェックをつける可能性もあります。

総じて、識別力が低い質問項目３は、「回答者のスキル開発意欲がどの程度あるのか」の判断に使いにくいのです。

このように、各質問が測定したい概念の程度をうまく識別して測定できる程度の違いは、識別力の大きさで数値化されます。

リッカート法による測定の場合：段階反応モデル

ここまでの説明は、質問に対してチェックを入れる、いわゆる２択の回答方式に基づいたものです。一方で、組織サーベイでよく用いられるのは、「０．まったくあてはまらない～４．非常にあてはまる」のように、複数の段階的な選択肢からひとつを選ぶ回答方式でしょう。これは、リッカート法と呼ばれる様式です。

図 12　リッカート法でスキル開発意欲を測定する場合の例

リッカート法で測定されたデータに対しても、項目反応理論では項目特性曲線を描く統計モデルが存在し、それを段階反応モデル（Samejima, 1969）と呼びます。このモデルで描かれる項目特性曲線[3]では、選択肢がそれぞれ選ばれる確率をグラフで表現します。

なお、各選択肢の順序は分析において考慮されますが、各選択肢に割り振られている数値は考慮されません。各選択肢の数値がどうであれ、段階反応モデルの分析は適用できます。 

リッカート法で測定した質問項目１「仕事で必要とされる資格を取るべく、勉強している」の回答データを想定して、段階反応モデルによって推定された項目特性曲線を見てみましょう。なお、繰り返しになりますが、グラフは架空例であり、実際のデータで推定されたものではありません。

図 13　リッカート法で測定した質問項目１の項目特性曲線（架空例）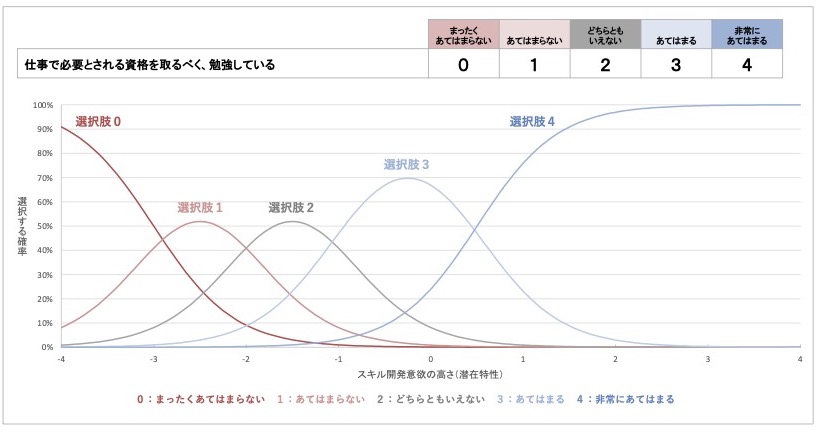

この例のように５つの選択肢があるならば、それぞれの選択肢に対して「その選択肢を選ぶ確率」がグラフ化されます。したがって、５つの選択肢があると、曲線が５本出現することになります。

段階反応モデルによる項目特性曲線でも、考え方は先ほど紹介したものと同様です。各選択肢について、それが選ばれる確率と測定したい概念の程度の対応関係が曲線で表現されています。選択肢ごとにそれを確認してみましょう。 

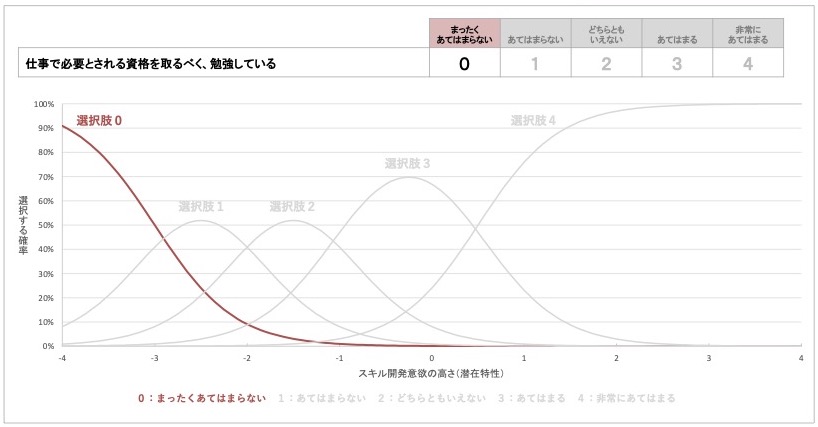
図 14　『まったくあてはまらない』を選ぶ確率とスキル開発意欲の高さの対応

質問項目１の選択肢『まったくあてはまらない』の項目特性曲線は、スキル開発意欲の潜在特性が－3点で選ぶ確率が50％となり、そこを下回る範囲でこの選択肢を選ぶ確率が高くなっています。 

この結果から、質問項目１の選択肢『まったくあてはまらない』は、スキル開発意欲が－3点、つまりスキル開発意欲が1000名中最下位レベルの人で、選ばれる可能性が高いと解釈できます。逆に、最下位レベルを上回るスキル開発意欲を持つ人は、この選択肢を選ぶ確率が低くなることも読み取れます。

これを質問内容で置き換えると、「必要な資格を取るために勉強している」ことに対しては、スキル開発意欲がとてつもなく低い人でない限り、『まったくあてはまらない』を選ぶことはほとんどないと考えられます。

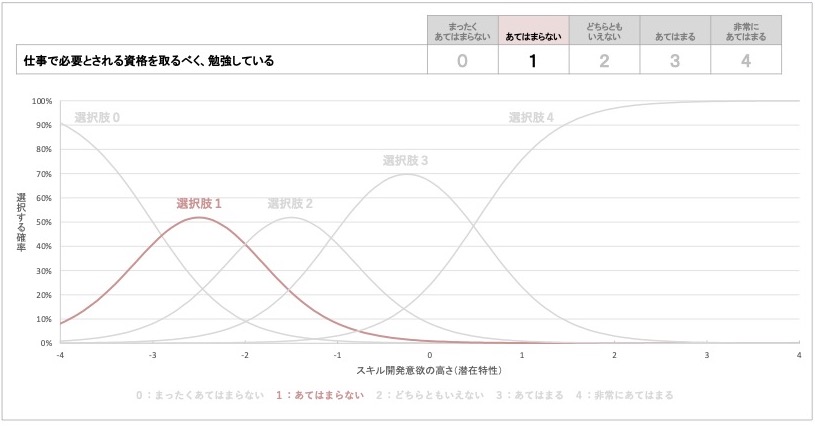
図 15　『あてはまらない』を選ぶ確率とスキル開発意欲の高さの対応

次に、質問項目１の選択肢『あてはまらない』は、項目特性曲線が山のような形状となっています。この選択肢では、スキル開発意欲の潜在特性が－2.5点で選ぶ確率が50%強と最大となり、そこから離れるほど、この選択肢を選ぶ確率が低くなることが読み取れます。

この結果から、質問項目１の選択肢「『あてはまらない』は、スキル開発意欲が－2.5点、つまり1000名中993位程度の高さの人で、選ばれる可能性が高い」と解釈できます。

必要な資格を取るために勉強していることに『あてはまらない』を選ぶのは、スキル開発意欲が最下位レベルとまではいかないが非常に低い人であると、この結果から予想されます。

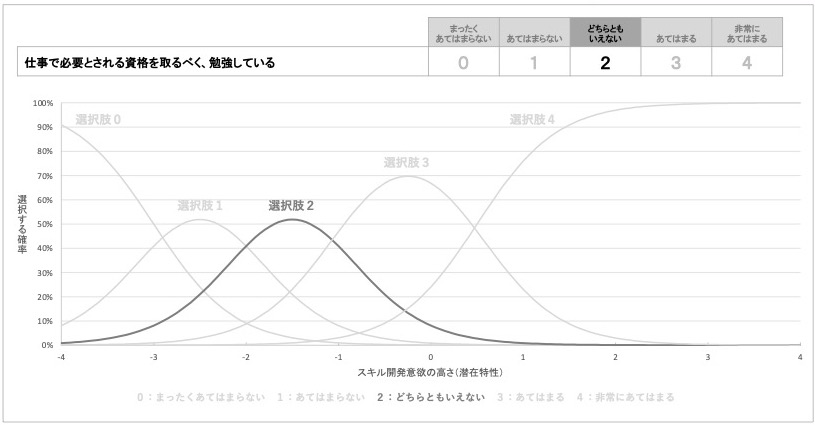
図 16　『どちらともいえない』を選ぶ確率とスキル開発意欲の高さの対応

続けて、質問項目１の選択肢『どちらともいえない』の項目特性曲線を見てみましょう。この選択肢では、スキル開発意欲の潜在特性が－1.5点で選ぶ確率が50%強と最大となり、そこから離れるほど、この選択肢を選ぶ確率が低くなることが読み取れます。

この結果から、質問項目１の選択肢「『どちらともいえない』は、スキル開発意欲が－1.5点、つまり1000名中933位程度の高さの人で、選ばれる可能性が高い」と解釈できます。

「必要な資格を取るために勉強している」ことに対しては、スキル開発意欲の程度がかなり下位の従業員が、『どちらともいえない』と中立的回答を選ぶと考えられます。

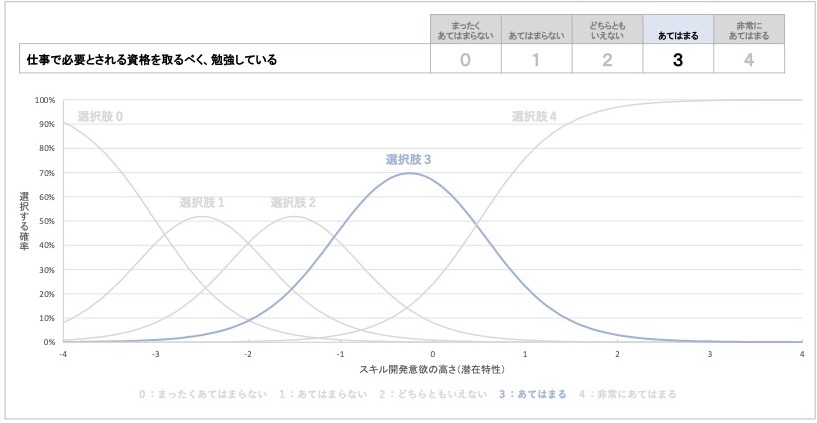
図 17　『あてはまる』を選ぶ確率とスキル開発意欲の高さの対応

そして、質問項目１の選択肢『あてはまる』の項目特性曲線は図17になります。この選択肢では、スキル開発意欲の潜在特性が－0.5点で選ぶ確率が約70%と最大になり、そこから離れるほど、この選択肢を選ぶ確率が低くなることが読み取れます。

この結果から、質問項目１の選択肢「『あてはまる』は、スキル開発意欲が－0.5点、つまり1000名中691位程度と、平均より少し低いスキル開発意欲を持つ人で、選ばれる可能性が高い」と解釈できます。

「必要な資格を取るために勉強している」ことに『あてはまる』を最も選びやすいのは、スキル開発意欲が平均を少し下回る程度の人だとわかります。スキル開発意欲が特別高い人でなくても、この質問には『あてはまる』とやや肯定的な回答を選ぶ可能性が高いことが、このグラフから把握できます。

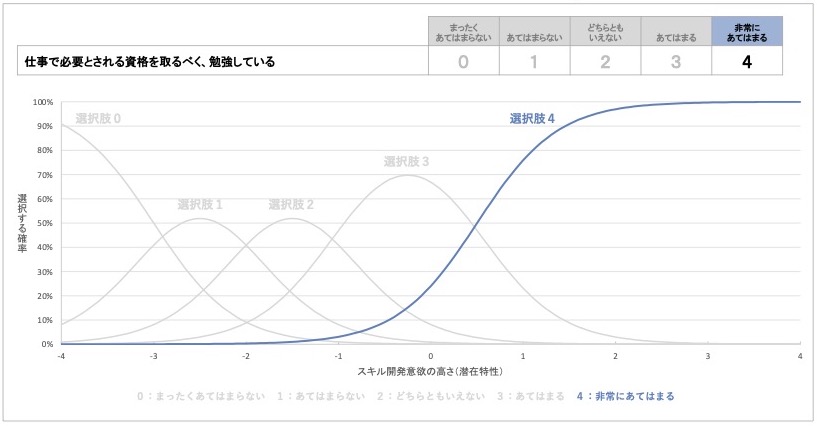
図 18　『非常にあてはまる』を選ぶ確率とスキル開発意欲の高さの対応

最後に、質問項目１の選択肢『非常にあてはまる』の項目特性曲線を見てみましょう。このグラフは、最初に見た項目特性曲線と同じ形状で、読み取り方も同じです。

この選択肢では、スキル開発意欲の潜在特性が＋0.5点で選ぶ確率が50%を超え始め、それを上回るほどこの選択肢を選ぶ確率が高くなることが読み取れます。

この結果から、質問項目１の選択肢『非常にあてはまる』は、スキル開発意欲が＋0.5点、つまり1000名中309位程度の高さと、平均より少し高いスキル開発意欲を持つ人で、選ばれる可能性が高いと解釈できます。

「必要な資格を取るために勉強している」ことは、平均より少し高い程度のスキル開発意欲を持つ人でも『非常にあてはまる』と強い肯定的回答を選びやすいとわかります。スキル開発意欲が非常に高い人でなくても、もっとも得点が高い選択肢を選ぶ可能性が高いということです。

このように、段階反応モデルを用いた項目特性曲線を描くことで、質問項目の選択肢ひとつひとつについて、スキル開発意欲の高さとその選択確率の対応を見ることができます。それにより、各質問項目の測定性能が、その選択肢レベルで細かく検証できるのです。

段階反応モデルにおける識別力と困難度

段階反応モデルでも、項目特性曲線を描くに際に用いられる、その項目特性関数には識別力と困難度が含まれます[4]。考え方は、最初に示した２パラメタ・ロジスティックモデルとおおよそ同じです。

なお、段階反応モデルにおける識別力は、全てのグラフに共通する値をひとつだけ定めると決められています。リッカート法で測定したスキル開発意欲の例では、５本の曲線グラフに共通する識別力がひとつだけ推定されることになります。

識別力が高い場合、回答者の潜在特性の程度を各選択肢がうまく識別できることを表します。そのとき、項目特性曲線は各選択肢のグラフが急斜面になります。

図 19　識別力が高い質問項目１の項目特性曲線（図 13の再掲）

先の質問項目１の項目特性曲線全体が、それに該当する識別力が高いグラフの例です。識別力が高いと、段階反応モデルによる項目特性曲線の傾きは急になり、「この選択肢が選ばれる確率が高いのは、潜在特性がこのくらいの程度の人だ」と、はっきりしやすくなるのです。 

これについては、むしろ識別力が低い場合を見てみるとよくわかるでしょう。識別力が低い質問項目３の項目特性曲線を見てみましょう。

図 20　識別力が低い質問項目３の項目特性曲線

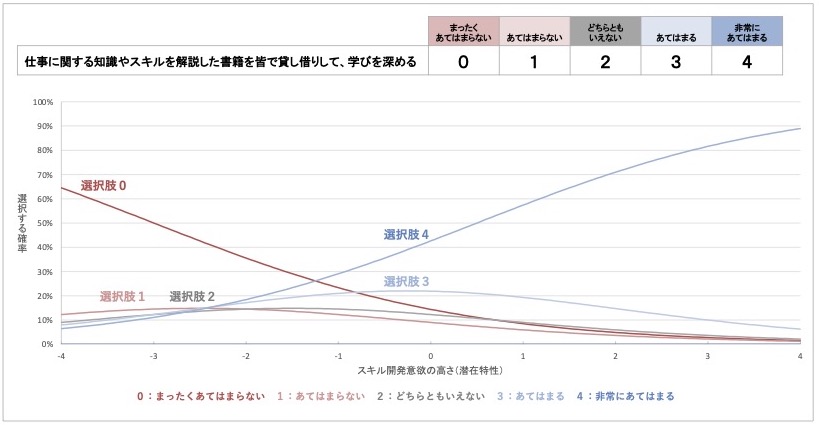
識別力が低い質問項目３の項目特性曲線では、各選択肢のグラフがきれいな山状になっておらず、広い範囲でグラフが重なっています。

大まかには、スキル開発意欲の潜在特性が－２点を下回るあたりで『まったくあてはまらない』、－１点を超えるあたりで『非常にあてはまる』が選ばれる確率が相対的に高く見えます。しかし、他の選択肢はスキル開発意欲の程度にかかわらず選択確率が10～20％あることも読み取れます。

このように、識別力が低い質問項目は、各選択肢の選択確率と、測定したい概念の潜在特性の高さがうまく対応しません。

例えば、スキル開発意欲の潜在特性が－1点程度の人では、『非常にあてはまる』を選ぶ可能性が最も高くはありますが、『まったくあてはまらない』を選ぶ可能性も高く、他の選択肢を選ぶ可能性も多少存在します。スキル開発意欲の潜在特性に対して、どの選択肢を選ぶ可能性が高いのか、はっきり対応しません。

スキル開発意欲の高さと選択肢を選ぶ確率が対応していないならば、この質問項目で選ばれた選択肢は、回答者のスキル開発意欲の程度をうまく反映していないことになります。各選択肢が、回答者のスキル開発意欲の高さを弁別できていないのです。

このように、段階反応モデルでも、識別力は各質問項目が回答者の潜在特性の高さをうまく識別できる程度を表します。

続けて、段階反応モデルの困難度です。２択の質問項目と異なり、段階反応モデルによって推定される困難度は、選択肢の個数だけ存在することが特徴です[5]。質問項目１の項目特性曲線で、困難度がグラフ上でどう表れるか確認してみましょう。

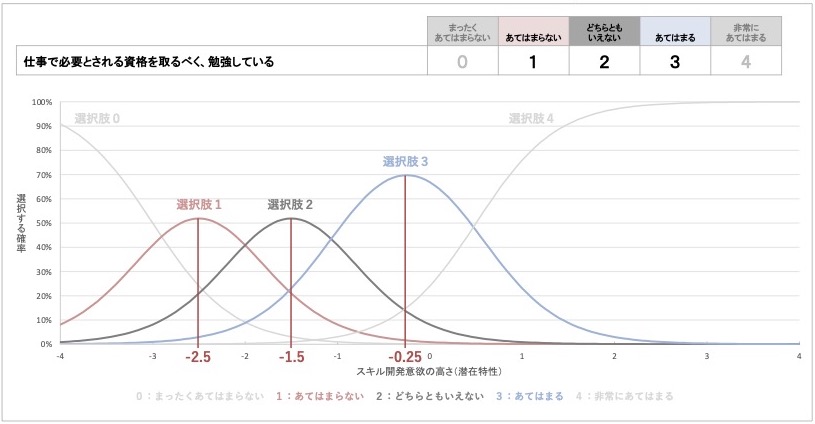
図 21　質問項目１の項目特性曲線における困難度（選択肢１，２，３）

グラフが山状になっている選択肢では、山の頂点にあたる潜在特性の値が各選択肢の困難度となります。この項目特性曲線の場合、選択肢１の困難度は－2.5点、選択肢２の困難度は－1.5点、選択肢３の困難度は－0.25点と読み取れます。

グラフの山の頂点は、各選択肢が選ばれる確率が最も高い点になります。そのことから、山状の曲線となっている選択肢の困難度は、「各選択肢が選ばれる確率が最も高い潜在特性の値」と言い換えることができます。

図 22　質問項目１の項目特性曲線における困難度（選択肢0，4）

それに対して、両端にある二つの選択肢では、困難度はそれらの選択肢が選ばれる確率が50％となる際の潜在特性の値になります。端の選択肢は必ずグラフが坂状になり、山の頂点が存在しません。そのため、最初に解説した２パラメタ・ロジスティックモデルにおける項目特性曲線と同じ方法で、困難度を定めます。

この項目特性曲線では、選択肢０の困難度は－3点、選択肢４の困難度は＋0.5点と読み取れます。

質問項目１は、最も肯定的な『非常にあてはまる』選択肢であっても、その困難度は＋0.5点、つまりスキル開発意欲が平均を少し超えた程度の従業員であれば、この選択肢を選びやすいことがわかります。

このことから、質問項目１は、潜在特性がそこまで高くなくても容易に高い得点の選択肢を選びやすい、つまり困難度が低い質問項目だと判断できます。

続けて、困難度が高い質問項目２の項目特性曲線を見てみます。比較がしやすいよう、質問項目１と同じ識別力で、困難度の値が異なるグラフにしてあります。

図 23　質問項目２の項目特性曲線における困難度

質問項目２のグラフは、質問項目１と比べて、曲線が全体的に右側にあることがわかります。これは、スキル開発意欲がかなり高くないと、肯定的な選択肢を選ぶ確率が高くならないことを表しています。

したがって、質問項目２は、高い得点の選択肢を選ぶためには非常に高いスキル開発意欲が必要である、つまり困難度が高い質問項目だと判断できます。

ここで、スキル開発意欲が＋0.5と平均より少し高い程度の従業員が回答した場合、質問項目１と２にどのように回答するかを、２つの項目特性曲線から予測してみましょう。

図 24　質問項目１と２の項目特性曲線（スキル開発意欲＋0.5付近の曲線に着目）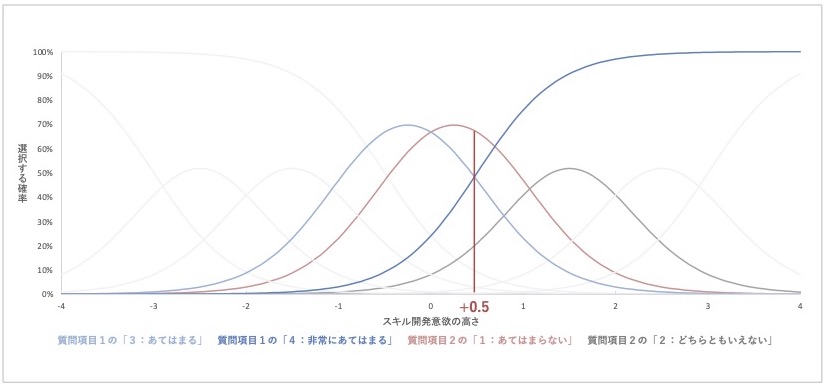

質問項目１では、スキル開発意欲の潜在特性が＋0.5程度で、ちょうど『あてはまる』か『非常にあてはまる』を選ぶ確率50％ずつとなります。要するに、質問項目１は「スキル開発意欲が平均より少し高い程度の回答者では、『あてはまる』以上の肯定的回答が選ばれる」と解釈できます。

一方、質問項目２では、その程度のスキル開発意欲でもっとも選ばれる可能性が高い選択肢は『あてはまらない』です。それに加えて、低い確率ながら『どちらともいえない』が選ばれるかもしれないと読み取れます。困難度の高い質問項目２は、平均より少し高い程度のスキル開発意欲では、肯定的な選択肢が選ばれないのです。

段階反応モデルにおける困難度も、各質問項目が捉えるスキル開発意欲の高さの違いを表現するものになっています。特に、質問の選択肢レベルでその違いを表現していることが大きな特徴です。 

以上のように、段階反応モデルでも、識別力と困難度が推定されることで項目特性曲線が描かれます。その項目特性曲線から、各質問項目の測定性能を詳しく把握することができるようになるのです。

偏った質問項目への対処

項目反応理論を活用した分析により、各質問項目の測定性能がグラフで可視化され、その違いを検証できます。これにより、うまく測定ができていない質問項目を把握し、対処することが可能となります。

まず、識別力が低い質問項目は「得点が測定したい概念の高低をうまく捉えられない」として、積極的に除外する判断をして良いでしょう。このような項目が得点化に含まれると、測定したい概念を正確に捉えにくくなります。

Baker(2001)では、識別力が0.65を超えると中程度の値、1.35を超えると大きな値と判断できるとされています。質問項目１と２の項目特性曲線は識別力が1.35としたグラフです。なお、筆者は、おおよそ1.00を超える程度の識別力があれば良いと考えています[6]。

他方、先ほどの質問項目１と２の例のように「困難度が大きく違っている項目がある」場合は、どのように考えればよいのでしょう。困難度が異なる質問項目は、各選択肢が捉える測定したい概念の高さが異なっています。そのため、それらを単純に平均して合算した値を用いて良いか、不安になるかもしれません。

これについては、２つの考え方ができます。ひとつは「あまり気にせず得点化してしまう」という考え方、もうひとつは「項目反応理論に基づいた得点化手法を用いて得点を算出する」という考え方です。

ひとつめの「あまり気にせず得点化してしまう」ことですが、項目反応理論による分析結果は測定性能の現状把握のためのものと割り切り、得点化には活かさない方針です。これは諦めにも見えますが、合理的な判断と言える部分も多少はあります。

というのも、十分に識別力が高く困難度が選択肢ごとに離れている質問項目であれば、各質問項目で選ばれる選択肢は、潜在特性の大きさに応じてある程度決まってくるからです。

先ほどの質問項目１と２に対して様々な潜在特性の高さの回答者を想定し、項目特性曲線から回答値を大まかに予測すると、以下のようになります。ここでは、各潜在特性の値において、選ばれる可能性が高い選択肢を１つずつピックアップしています。

図 25　潜在特性の高さに応じた、質問項目１と２で選ばれる可能性が最も高い選択肢と予想得点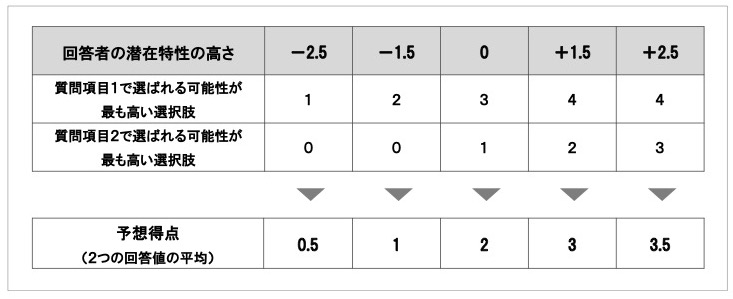

各質問項目への回答は、潜在特性の高さによって、選ばれる可能性が高い選択肢が異なります。また、２つの質問項目の項目特性曲線を見ると、「困難度が低い質問項目１で低得点の選択肢が選ばれ、同時に、困難度が高い質問項目２で高得点の選択肢が選ばれる」ことは、確率上ほぼありえないと考えられます。

そして、回答者の潜在特性が高いほど、予想得点（各質問で選ばれる可能性が高い選択肢の得点を平均した得点）も、高いことがわかります。困難度が異なり各質問項目の選択肢が違う潜在特性の程度を捉える構成でも、算出される指標の得点（回答値の平均や合計）は、おおよそ潜在特性の程度と対応するのです。

とはいえ、これはあくまで確率上、そうなる可能性が高いというだけの話です。各質問項目の項目特性曲線を見ると、選ばれる可能性が高い選択肢でも、その確率は他と比べて相対的に高い程度でしかないとも言えます。つまり、予想得点からずれた得点になる可能性も十分にあり、確実性がやや低い問題はどうしても残ります。 

例えば、潜在特性の高さが－2.5のとき、質問項目１で最も選ばれる可能性が高いのは『１：あてはまらない』ですが、その確率は50％強です。加えて、『０：まったくあてはまらない』『２：どちらともいえない』が選ばれる可能性もそれぞれ20％強あり、回答値が１点でなく、０点や２点となる可能性も多少はあります。

そこに不満や心配を感じ、「測定したい概念について、より正確な各回答者の得点を算出したい」と考えるなら、ぜひもう一つのアプローチに挑戦しましょう。そのアプローチとは、項目反応理論による分析結果を活かした得点化の方法を用いることです。

項目特性曲線の基である項目特性関数を用いて、各質問項目で選んだ選択肢から予測される、回答者の潜在特性の高さを推定する方法が存在します。計算がかなり複雑になるためここでの解説は割愛しますが[7]、この方法を用いれば、各質問項目で各選択肢が選ばれる確率と潜在特性の値の対応まで加味して、得点計算ができます。

後者の方法は、得点計算において各質問項目の困難度や識別力が考慮されているため、単純に平均を取るより厳密な得点計算が可能です。

例えば、通常の得点化方法だと、質問項目１に『３：あてはまる』、質問項目２に『１：まったくあてはまらない』と選ぶ回答者と、質問項目１と２の両方とも『２：どちらともいえない』と選ぶ回答者では、回答値の平均は２と同じであり、同じ得点が付与されます。

他方、項目反応理論を用いた得点化では、各質問項目で識別力や困難度を細やかに推定し、それに基づいた得点を計算します。その結果、上記のような平均で算出する得点が同じになる状況でも、回答者間の違いを表す得点化が可能となるのです。

また、先ほど除外すべきとした識別力が低い質問項目についても、問題をある程度改善して得点を計算することができるメリットがあります。その意味でも、項目反応理論を用いて得点を計算する方が、より望ましいと言えるでしょう。

ただし、項目反応理論を用いた各指標の得点算出には、困難度や識別力を正確に推定する必要があります。そのためには、後述する様々な注意点を乗り越える必要があります。この方法を採用した得点計算がしたいならば、それに向けたサーベイ設計が重要です。

項目反応理論の注意点

一次元性と局所独立性の仮定を満たす必要がある

一次元性とは、ある概念を捉える各質問項目への回答が、測定したい概念をあらわす共通因子[8]１つのみで定まることを指します。つまり、複数の項目に対して複数の概念を想定した因子モデルでなく、複数の項目に対して１つの概念のみですべてが説明される因子モデルが前提となっています。 

また、局所独立性の仮定とは、各質問項目への回答間の相関関係が、測定したい概念の程度のみで説明され、それを除けば各質問項目の回答値は互いに無関連になることを指します[9]。

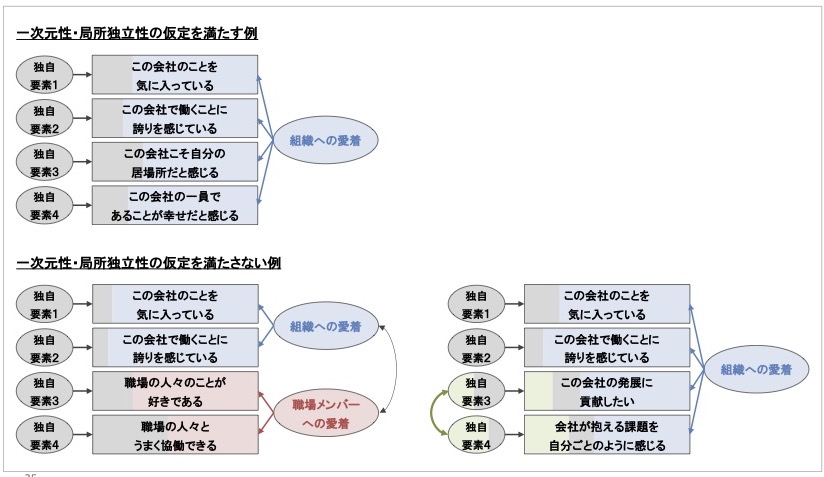
これは、確認的因子分析における１つの共通因子で全ての項目を説明する因子モデルと同様のモデルです。以下に良い例と悪い例を架空例で示します。ここでは、「組織への愛着（＝組織（会社）に対する温かな結びつきの感覚）」を測定するものとして、質問項目４つを構成しています。 

図 26　一次元性と局所独立性を満たす場合と満たさない場合

図26の上にある因子モデルが統計学的に認められるならば、複数の質問項目間の相関関係が１つの共通因子のみで説明されていると見なせます[10]。ここから外れる悪い例が、左下と右下にある因子モデルです。

左下のモデルでは、組織への愛着という一つの概念を測定する予定だった４つの質問項目に対して、２つの共通因子の存在が認められたモデルになっています。この状況では、４項目の得点が１つの概念のみに左右されているとはいえず、一次元性の仮定を満たしません。

また、右下のモデルでは、４つの質問項目の得点が１つの共通因子により左右されることは示されていますが、一部の質問項目の間に、得点が対応する要素が残っている状態です。これら２つの項目は、組織への愛着を捉えると同時に組織への貢献意思も問う質問内容であり、その要素が相関していると考察できます。

その要素が何にせよ、これら２つの質問項目は「組織への愛着とは異なる概念によって、得点同士が関連を持っている」状態であり、これは局所独立性の仮定を満たさない状態です。

このように、項目反応理論を用いた分析を行う場合は、「各質問項目が、定義とずれた内容を含まずに、狙い通りひとつの概念を測定できている」ことが必須になります。そのためには、サーベイ設計時に質問項目をしっかり作りこみ、質問内容やニュアンスを洗練させることが不可欠です。 

多くのサンプルサイズが必要

項目反応理論による分析を行うためには、多くのサンプルサイズ（回答者の人数）が要求されます。特に、項目反応理論は、質問項目の選択肢レベルで詳細に特徴を捉える分析であるため、正確な推定計算のために要求されるサンプルサイズも大きくなります。

Embretson & Reise (2000)は、リッカート法のような複数の選択肢を持つ尺度に対して段階反応モデルの正確な推定を行うには、最低でも250名必要であり、推奨されるサンプルサイズは500名以上だと述べています。

厳密な検証方法である項目反応理論を使うならば、これらの注意点を踏まえ、サーベイの作成段階から質問内容の構成やサンプルサイズの計画をしっかり組むことが必要です。 

本コラムでは、項目反応理論を紹介しました。回答者の特徴をより正確に捉えるために、知っておくと有益な解析手法です。

 

引用文献

Baker, F. B. (2001). The basics of item response theory (2nd ed.). ERIC Clearinghouse on Assessment and Evaluation.

Embretson, S. E. & Reise, S. P. (2000). Item Response Theory for Psychologists. Lawrence Erlbaum Associates.

Hambleton, R. K., & Swaminathan, H. (1985). Item response theory: Principles and applications. Springer Science & Business Media.

加藤 健太郎・山田 剛史・川端 一光 (2014).　Rによる項目反応理論　オーム社

Samejima, F. (1969). Estimation of Latent Ability Using a Response Pattern of Graded Scores (Psychometric Monograph No. 17). Richmond, VA: Psychometric Society. Retrieved from http://www.psychometrika.org/journal/online/MN17.pdf

鈴木 綾子・豊田 秀樹・小杉 正太郎 (2004). 項目反応モデルによるストレス反応尺度の構成とテスト特性曲線によるその深化の過程 心理学研究, 75(5), 389-396.

豊田 秀樹 (2012). 統計ライブラリー 項目反応理論［入門編］（第２版）朝倉書店

脚注 

[1] 本コラムの内容をより深く理解するには、確認的因子分析の知識が必要です。確認的因子分析は、当社コラム「確認的因子分析とは何か」で解説しています。

[2] 項目反応理論が捉える潜在特性は、平均０, 標準偏差１を母数とする標準正規分布を仮定しており、以降に示す割合の解説は、標準正規分布表を参照した値です。

[3] 段階反応モデルでは、項目特性曲線に該当する図 12のようなグラフは、「カテゴリ反応曲線（category response curve）」「カテゴリ確率曲線（category probability curve）」などカテゴリに対する反応を強調する名称で呼ぶ方が一般的です。本コラムでは、実務家向けに説明を簡略化するため、全て「項目特性曲線」と統一しています。

[4] 複数選択肢を持つ質問項目では、一度の計算で項目特性曲線を選択肢ごとに描くことが難しいという問題があります。そこで、段階反応モデルでは、「ある選択肢以上を選ぶ確率」を２パラメタ・ロジスティックモデルと同様の方法で計算します（境界特性関数）。そして、「（ある選択肢以上を選ぶ確率）－（次の選択肢以上を選ぶ確率）」を計算することで、各選択肢の項目特性関数を作成しています。例えば、選択肢２番を選ぶ確率の項目特性関数は「（選択肢２番以上を選ぶ確率）－（選択肢３番以上を選ぶ確率）」で算出されています。

[5] 本コラムでは、項目特性曲線において解釈がしやすいことから、豊田（2012）で示された段階反応モデルにおける位置母数を、困難度として取り上げています。他方、研究論文では、注釈４で述べた境界特性関数において「ある選択肢以上を選ぶ確率が50％となる潜在特性の値（境界特性値）」を、困難度の指標として報告することも多いです。これらの違いについて、詳しくは豊田（2012）を、境界特性値から段階反応モデルにおける位置母数を算出する方法のみならば鈴木他（2004）を参照してください。

[6] 項目反応理論における識別力は、回答データを順序尺度と見なした、確認的因子分析で算出される因子負荷量αから「α/√(1-α²)」で計算できるという特徴があります。この式に基づくと、識別力1.00となる因子負荷量の値は.704になります。筆者はこの値を、「複数項目の内容的妥当性を確保するバリエーションを保ちつつ、程よい大きさの因子負荷量であり、項目特性曲線もある程度きれいに描ける値」と経験的に捉えており、識別力1.00を基準として好んで用いています。

[7] この計算方法としてのEAP推定法を、専門用語を用いつつ簡単にまとめると、次のようになります。（１）（局所独立性の仮定が満たされている前提で）回答者が各質問項目で選んだ選択肢の項目特性関数をかけ算した数式（尤度関数）を作成する。（２）尤度関数に、事前分布として標準正規分布を仮定したベイズの定理を適用し、その回答者の潜在特性の事後分布を構成する。（３）事後分布に基づいて、潜在特性の期待値を算出し、それをその回答者の潜在特性の値とする。詳細な計算過程に興味のある方は、加藤他（2014）をご覧ください。

[8] 共通因子や次に示す因子モデルについては、当社コラム「確認的因子分析とは何か」で解説しています。

[9] より厳密には、局所独立性は、潜在特性をひとつの値に固定したとき、各質問項目への回答が互いに独立であることを指します（加藤他, 2014）。

[10] 厳密には、一次元性の確認として、１つの共通因子のみで複数の項目が説明される因子モデルを検証することは不十分です。複数の質問項目から算出されたカテゴリカルデータとしての相関行列に対して、固有値を算出して因子数を検討し、１因子解が妥当だと確認する方法が確実です（加藤他, 2014）。

---

 執筆者

能渡真澄

株式会社ビジネスリサーチラボ フェロー。信州大学人文学部卒業，信州大学大学院人文科学研究科修士課程修了。修士（文学）。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を、他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており、通常では捉えることが困難な、様々なデータの背後にある特徴や関係性を分析・可視化し、その実態を把握する支援を行っている。