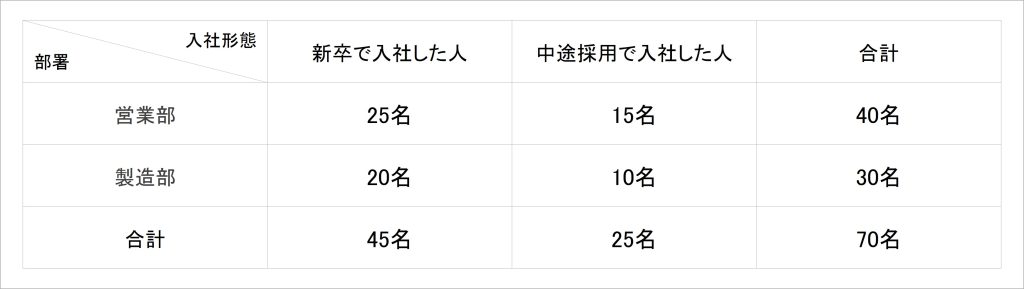
社内の人事データや組織サーベイの集計結果を表す方法として、「クロス集計表」がよく使われます。クロス集計表とは、2つの指標をそれぞれ行・列に設定し、集計した表のことです。たとえば、「部署ごとの、新卒で入社した人・中途採用で入社した人の数」を表したクロス集計表は表1のようになります。

 表1：部署ごとの新卒入社者・中途採用者のクロス集計表

クロス集計表を用いることで、結果をシンプルに表すことができます。しかし、例えば「営業部と製造部で、中途者の数に違いはあるのだろうか」と考えたとき、クロス集計表の数字を見ただけでは、本当に注目すべき差かどうかは判断できないのです。

 クロス集計表における数値の差は、本当に注目すべき差かどうか。それを検証する方法の一つとして「カイ二乗検定」があります。本コラムでは、このカイ二乗検定の実施方法、その魅力と限界について説明します。 

ステップ1：独立性の検定

 カイ二乗検定は、「独立性の検定（※1）」と「残差分析」という２つのステップに分かれています。まず、独立性の検定について説明します。

 独立性の検定を一言で表すと、「カテゴリカルな2つの指標が、お互いに独立している（関連性がない）のか、それとも独立していない（関連性がある）のか」を明らかにする検定です。

 ここで言う「カテゴリカルな指標」とは、性別（男・女）や、色（青・赤・黄）など、主に分類に用いられ、数値のように計算できない（男―女＝？ 青×赤＝？のように）指標のことを指します。部署（営業部・製造部など）も、カテゴリカルな指標です。

 例えば、「営業部と製造部で、新卒で入社した人・中途採用で入社した人の数がかなり異なっている気がする。実際に注目すべき差なのかどうかを調べたい」と考えたとします。

 これを独立性の検定に沿って考えると、「部署（営業部か製造部か）と、入社形態（新卒者か中途者か）という2つの指標が、互いに独立しているのか、独立していないのか」について検討することになります。

 独立していれば（関連性がなければ）「部署間で人数に目立った差があるとはいえない」、独立していなければ（関連性があれば）「部署によって人数が異なる」ということになります。

 独立性の検定を含め、統計分析を行う際には、まず2つの仮説を立てる必要があります（※2）。一つは「帰無仮説」と呼ばれるものです。独立性の検定における帰無仮説は、「2つの指標は互いに独立している（関連性がない）」ということになります。先ほどの例を当てはめると、帰無仮説は「部署と入社形態は独立している」、つまり「部署によって、新卒者・中途者の人数に目立った差はない」ということです。

 もう一つの仮説は「対立仮説」と呼ばれ、帰無仮説を否定するように立てる仮説です。独立性の検定における帰無仮説は、「2つの指標は独立していない（関連性がある）」ということになります。例を当てはめると、対立仮説は「部署と入社形態は互いに独立していない」、つまり「部署によって、新卒者・中途者の数に違いがある」となります。

 もともと関心のあった「営業部と製造部で、新卒者・中途者の数が異なっている気がする」という考えは、まさに、この対立仮説にあたります。

 独立性の検定では、帰無仮説が正しい前提の下で、手元のデータの検証を行います。そして、もし帰無仮説を否定する（“関連性がない”ということはない）ような結果が出れば、帰無仮説を棄却し、対立仮説を採択するというプロセスをたどります。まとめると図1のとおりです。

図1：カイ二乗検定における帰無仮説と対立仮説

 では、実際の検定に入っていきたいと思います。検定の流れは、

• カイ二乗値（χ²）の算出
• カイ二乗分布を用いた、帰無仮説を棄却するかどうかの判断

となります。

 まず（1）カイ二乗値（χ²）の算出ですが、カイ二乗値は図2のような式で求められます。

 

図2：カイ二乗値の計算式

 この数式を言葉で表すと、「クロス集計表の、あるセルの観測度数を期待度数で引いたものを二乗し、それを期待度数で割ったものを、すべてのセル分合計する」ということになります。

 ここで新たに登場した、観測度数・期待度数について説明します。観測度数とは、「実際のデータとして得られた値」を指します。冒頭のクロス集計表に基づけば、営業部の新卒者の観測度数は25、製造部の中途者の観測度数は10となります。

 一方、期待度数とは、「二つの指標が互いに独立していた場合、そのセルに入ることが期待される値」です。つまり、「部署と入社形態が互いに独立している（関連性がない）場合、このセルにはこの人数が入るだろうと考えらえる値」を指します。

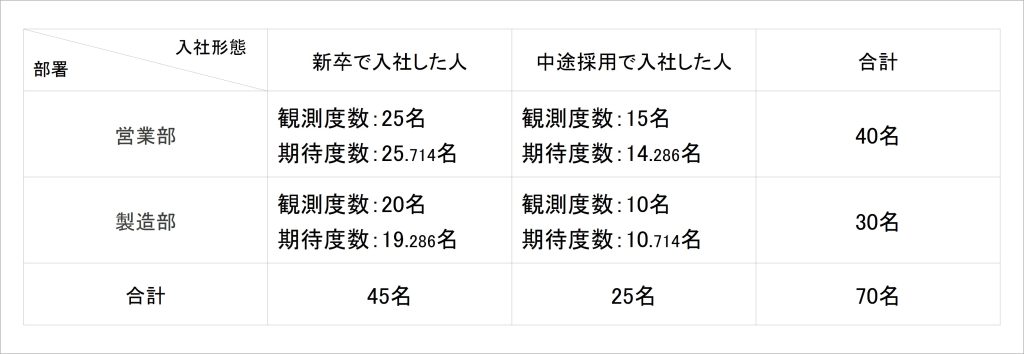
 各セルの期待度数を算出するためには、クロス集計表で合計が算出されている必要があります。冒頭の表に合計行・合計列を足したものが表2です。

表2：部署ごとの新卒入社者・中途採用者のクロス集計表(合計行・合計列追加）

 例えば、「営業部に新卒で入社した人」の期待度数について考えてみます。もし、部署と入社形態に関係がないとしたら、全入社者における新卒者・中途者の割合に合わせて、各事業部にも新卒者・中途者が割り振られていることになります。つまり、「全入社者における新卒者の割合と、営業部の入社者における新卒者の割合は同じ」ということです。実際に計算してみると、40×（45／70）=25.714（小数点第4位四捨五入）となります。

 このように、クロス集計表の各セルの期待度数を算出し、先ほどの観測度数と併記したものが表3です。

 表3：部署ごとの新卒入社者・中途採用者のクロス集計表（期待度数追加）

期待度数がわかれば、先ほどのカイ二乗値の数式に当てはめ、図3のようにカイ二乗値を算出することができます。カイ二乗値を大まかに表すと、「各セルの観測度数と期待度数のズレを算出し、それを足し合わせたもの」と言えるかもしれません。なお、このズレは「残差」とも呼ばれます（後述の「残差分析」で詳述）。

 この数式から、カイ二乗値は、観測度数と期待度数のズレが大きければ大きいほど値として大きくなることもわかります。つまり、カイ二乗値が高いほど、２つの指標は互いに独立しておらず、関連している可能性が高いということになります。

図3：部署×入社形態のクロス集計表におけるカイ二乗値の算出

 続いて、(2)カイ二乗分布を用いた、帰無仮説を棄却するかどうかの判断です。カイ二乗分布は端的に言うと、「帰無仮説を前提とした上で、あるカイ二乗値がどれくらいの発生確率で生じうるか」を規定したものです。

 これを用いることで、先ほど算出したカイ二乗値が、果たして「二つの指標が互いに独立していない（関連性がある）」と言えるほどの大きなズレであるかどうかを判断することができます。

 なお、このとき用いるカイ二乗分布は、自由度によって異なります。カイ二乗分布における自由度は、関係性を見たい二つの指標の、それぞれのカテゴリ数（事業部なら、営業部と製造部の「2」）から、それぞれ1を引いたものをかけ合わせて算出されます。つまり「（（合計列以外の）クロス集計表の列数-1）×（（合計列以外の）クロス集計表の行数-1）」となり、今回の例で言えば「（2-1）×（2-1）=1」となります。

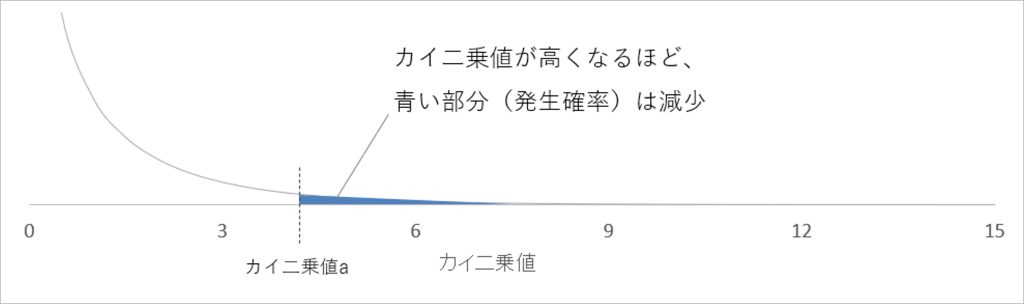
 自由度が1のカイ二乗分布をグラフで表すと、図4のようになります。グラフ内の青い部分は、カイ二乗値がaのときのカイ二乗値の発生確率です。カイ二乗値が高ければ高いほど、青い部分は減少します。つまり、そのカイ二乗値の発生確率が低くなるということです。

 ということは、青い部分が小さくなるようなカイ二乗値の高さであれば、あまり発生しない特徴的なカイ二乗値であるということがいえます。

図4：自由度1のカイ二乗分布図

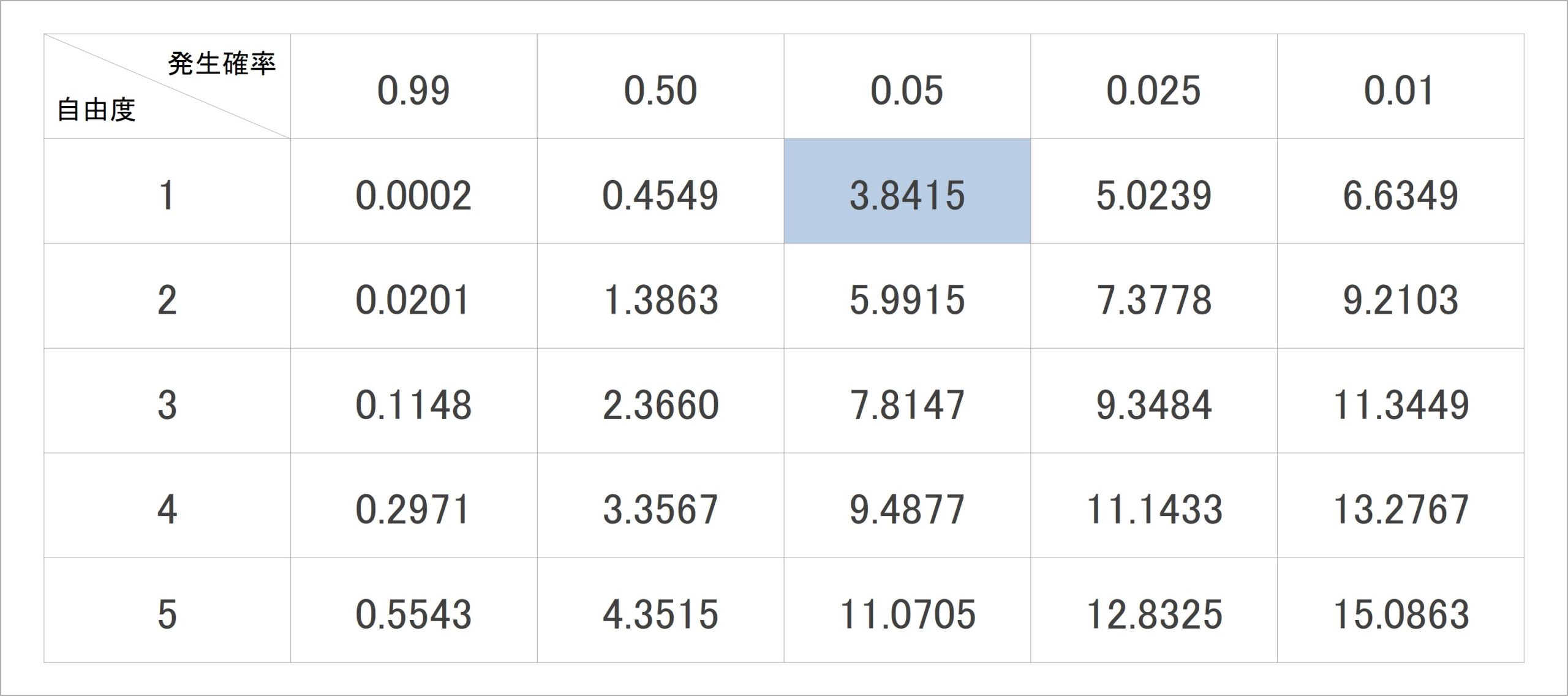
 では、どれくらいの高さのカイ二乗値であれば、あまり発生しない特徴的なものと言えるのでしょうか。これを調べるのに便利なのが、「カイ二乗分布表」と呼ばれるものです（表4）。

 この表では、列に自由度、行に発生確率が置かれ、ある自由度のとき、ある発生確率となるカイ二乗値を調べることが出来ます。表4に記載されているのはその一部で、web上や統計学の書籍では、発生確率や自由度がより多く記載されているものもあり、簡単に入手できます。

 カイ二乗検定における一般的な確率の基準として、0.05 (5%)未満、あるいは0.025(2.5%)未満が目安であるとされています。今回は0.05とし、0.05の列で自由度1の行を見てみると、3.8415（青い部分）とあります。つまりカイ二乗値が3.8415よりも高い時、そのカイ二乗値は5%未満の確率でしか発生しない、特徴的な値ということになります。

 表4：カイ二乗分布表

今回の例で算出されたカイ二乗値は0.130であり、これは3.8415よりも低い値です。ということは、特徴的でない、よく見られる値ということです。よって今回の例では「２つの指標は互いに独立している」という帰無仮説は棄却されず、「部署によって、新卒者・中途者の人数に目立った差はない」という結論が導き出せます。 

ステップ2：残差分析

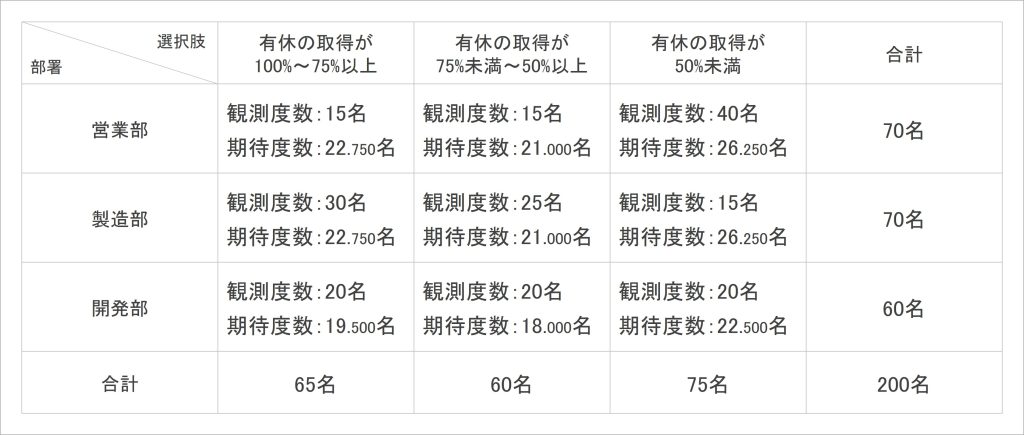
 続いて、有給休暇の取得状況を集計した表5の例を考えてみたいと思います。部署によって、有休取得状況に違いはあるのでしょうか。

 表5：有給休暇の取得状況

復習になりますが、この分析における帰無仮説は「有休の取得状況と部署は互いに独立している（関連性がない）」、つまり「有休の取得状況は部署によって違いがない」となります。また対立仮説は「有休の取得状況と部署は互いに独立していない（関連性がある）」、つまり「有休の取得状況は部署によって異なっている」ということになります。

 クロス集計表に基づいてカイ二乗値を算出した結果、19.963となりました。カイ二乗分布表（表4）から、自由度4（（部署数3-1）×（選択肢数3-1））のとき、発生確率が0.05であるカイ二乗値は9.4877です。ということは、今回の分析で得られたカイ二乗値はこの数値よりも高く、あまり見られない特徴的な高さであるということがわかります。

 よって帰無仮説は棄却され、対立仮説の「有休の取得状況は部署によって異なっている」という主張が支持できるということになります。

 有休の取得状況は部署によって異なっていることは分かりました。では、どの部署とどの部署の間に違いがあるのでしょうか。独立性の検定では「2つの指標が独立しているか否か」までは分かり、2×2のクロス集計表であれば事足ります。

 しかし、今回のようにいずれかの指標の水準数が3つ以上になった場合、「クロス集計表のどのセルの値が高い・低いと言えるのか」まではわかりません。そこで、「残差分析」が必要になります。

 残差分析とは、各セルの残差を確認し、残差が一定以上の値であれば、そのセルの観測度数は大きい（または小さい）と言うことができる分析です。残差分析は

• 残差の算出
• 調整済み標準化残差の算出
• 調整済み標準化残差の確認

という流れで行います。 

(1)残差の算出

残差とは、観測度数–期待度数で算出される値のことです。この計算は、既にカイ二乗検定の中でも行われています。再度カイ二乗検定の数式を確認すると（図5）、分子に観測度数－期待度数、つまり残差を算出する式が含まれていることが分かります。

図5：カイ二乗値の計算式に含まれる残差

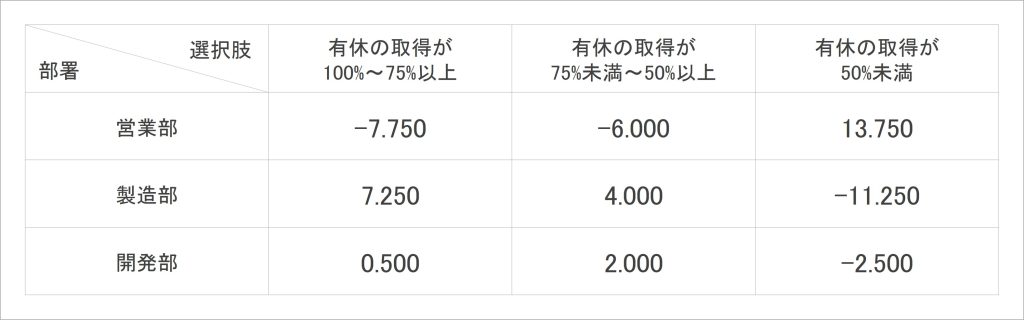
 実際に残差を算出してみると、表6のようになります。残差ですが、部署の人数差が大きい場合、その影響をけて値が大きくなってしまう可能性があるなど、このまま使用するには問題があります。

 表6：部署×有給休暇の取得状況のクロス集計表における残差

そこで(2)「調整済み標準化残差」を算出する必要があります。 

(2)調整済み標準化残差の算出

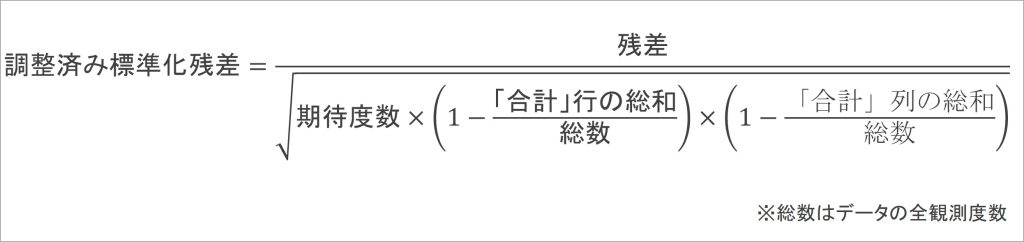
調整済み標準化残差とは、合計行と合計列の総和を用いて値を調整した上で、残差を標準化したものです。この残差は、各セルの元々の度数に影響を受けにくくなっています。

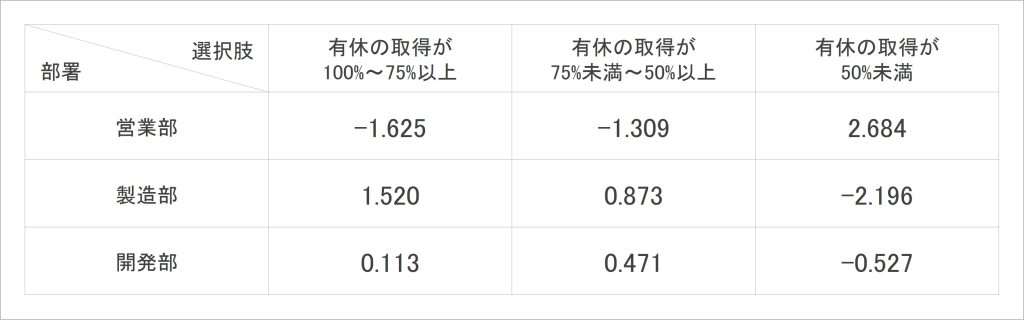
 具体的には、図6の数式で算出することが出来ます。この数式に従って、調整済み標準化残差を算出したものが表7です。表６よりも、セル間の幅が小さくなっていることがわかります。

図6：調整済み標準化残差の計算式

 表7：部署×有給休暇の取得状況のクロス集計表における調整済み標準化残差

(3)調整済み標準化残差の確認

調整済み標準化残差は、絶対値1.96以上のときに、あまり見られない特徴的な値であるとみなすことができます。表7の各セルを見ると、「営業部・有休の取得が50%未満」が1.96より高く、「製造部・有休の取得が50%未満」が-1.96より低いことがわかります。

 つまり、今回の有休の取得状況の集計結果でカイ二乗検定を行うと、

• 営業部は、有休取得50%未満の人が他部署よりも多い
• 製造部は、有休取得50%未満の人が他部署よりも少ない

ということが、統計的にいえるということになります。 

カイ二乗検定を使用する際のルール

 カイ二乗検定の使用には、いくつかのルールがあります。このルールに従わずにカイ二乗検定を用いることは、結果の信頼性を損ねる可能性がありますので注意しましょう（※3）。 

(1)クロス集計表内の各セルのデータは、人数または頻度である必要がある

 今回の例では、クロス集計表の各セルは、そこに当てはまる人数を表していました。このように、カイ二乗検定で用いるクロス集計表内のデータは、人数やなにかの頻度である必要があり、パーセンテージなどに変換されたデータは使用できません。 

(2)ある人は1つのセルにしか存在しないようなクロス集計表である必要がある

 たとえば、時期による有休取得率の変化を見ることなどを目的として、行に時期（4月・10月）、列に有休取得率（100％・75％・50％未満）を置いたクロス集計表を作成したとします。この場合、4月と10月の行に、同一人物が1回ずつ含まれることになります。つまり、同じ人がクロス集計表内の2つのセルに含まれるということです。

 このような場合、カイ二乗検定を用いることができません。カイ二乗検定を用いたい場合は、ある人は表内のある1つのセルにしか出現しない（合計列・行は除く）ようなクロス集計表を作成しましょう。 

(3)各セルの期待度数はクロス集計表内の80%で5以上であり、期待度数が1未満のセルは存在しないほうがよい

 期待度数が5を下回るセルが20％以上あるクロス集計表は、カイ二乗検定を用いるのに不適切とされています。基本的にカイ二乗検定を使用するには、観測度数（実際に測定される人数など）が多いほど良いのです。

 適切なクロス集計表かどうかを簡単に確認する方法として、クロス集計表の観測度数の総計が、クロス集計表のセル数（合計列・行は除く）に5をかけた値よりも高ければ、カイ二乗検定を用いても良いと考えることができます。たとえば、表1はセル数4×5=20ですが、観測度数の総計は70であるため、カイ二乗検定を用いても良いということになります。

 なお、期待度数が5を下回るセルが20%以上ある場合は、カイ二乗検定ではなく「フィッシャーの直接法」という検定手法を用いることで、独立性の検定と同じことを行うことができます。ただし、これは2×2のクロス集計表でしか用いることができないため注意しましょう。 

(4)セル数は20が限度

 (3)のルールと関連しますが、クロス集計表内のセル数が20を超えると、期待度数が5を下回る小さいセルが出てくる可能性も高くなるため、カイ二乗検定を用いることが不適切とされています。セル数は20以下になるようにクロス集計表を調整しましょう。

 水準が多すぎる場合は、まとめることも一つの手です。有休取得率で言えば、10%で区切ると10水準になってしまいますが、表5のように区切れば3水準にまとめることが可能です。 

カイ二乗検定の魅力と限界

 今回は、2つの指標の関連性を見出す方法としてカイ二乗検定をご紹介しました。カイ二乗検定の魅力の一つは、「カテゴリカルなデータを分析できる」というカイ二乗検定の性質それ自体です。

 たとえば、選択肢が「はい」「いいえ」の二者択一形式の質問への回答結果を、部署などのグループ間で比較出来ます。また、性別・役職・部署・資格の有無など、新たにアンケートを取らずとも、既に手元にある人事情報の中にカテゴリカルな指標は多く含まれていることでしょう。こういった指標に基づいて分析を行うことも可能です。

 今回は数式や専門用語なども挙げたため、難しい印象を持たれた方もいらっしゃるかもしれません。しかし、表計算ソフトの関数機能や統計ソフトなどを使用すれば、より簡単に、より見やすい結果としてカイ二乗検定を行うこともできます。

 一方、カイ二乗検定の限界の一つは「連続的な数量指標の分析ができない」ということです。例えば、身長と体重の関連性、年齢と学力テストの関連性を分析するということは出来ません。カイ二乗検定が対象とするカテゴリカルな指標（性別や部署など）は、和差積商といった計算ができないのに対し、連続的な数量指標はそれが行えます。

 このような連続的な数量指標間の関連性を明らかにするための分析手法の一つとして「相関分析」があります。相関分析であれば、身長と体重の関連性、年齢と学力テストの点数の関連性なども見ていくことが可能です。相関分析については、「人事のためのデータ分析入門：「相関」とは何か」でも詳しく説明しているのでご覧ください。 

脚注

※1：カイ二乗検定は独立性の検定のほかに、適合度の検定（データが理論的な分布と等しいか等しくないかを検定する手法）がありますが、本コラムでは、組織サーベイの結果や人事データの分析など実務に用いられることも多い独立性の検定について扱います。
※2：「統計的に有意」とはどういう意味かについては、詳しく説明している当社のコラムもご一読ください。
※3：McHugh, M. L. (2013). The chi-square test of independence. Biochemia medica, 23(2), 143-149.

編集履歴

（2023/09/19）読者から「表4に誤植がある」とご指摘をいただき、訂正いたしました。（誤）発生確率 0.25 →（正）発生確率 0.025

---

執筆者

小田切岳士

同志社大学心理学部卒業、京都文教大学大学院臨床心理学研究科博士課程（前期）修了。修士（臨床心理学）。公認心理師、臨床心理士。働く個人を対象にカウンセラーとしてのキャリアをスタートした後、現在は主な対象を企業や組織とし、臨床心理学や産業・組織心理学の知見をベースに経営学の観点を加えた「個人が健康に働き組織が活性化する」ための実践を行っている。特に、改正労働安全衛生法による「ストレスチェック」の集団分析結果に基づく職場環境改善コンサルティングや、職場活性化ワークショップの企画・ファシリテーションなどを多数実施している。