2022年6月6日
交互作用とは何か
本コラムでは「交互作用」について解説します。交互作用は、一度理解すれば様々な場面に対する見方が変わる重要な概念です。以下では、まず、交互作用の例を用いながら交互作用の定義や意義を確認します。その後、交互作用に対する理解を深めるために、交互作用と主効果の違いなどを確認します。最後に、実際に分散分析や重回帰分析で交互作用を検討した場合の様子を紹介します。
交互作用とは
交互作用の定義は、「ある要因が従属変数に及ぼす影響の方向(正の影響か負の影響か)または大きさ(どの程度の影響か)が、別の要因の水準によって異なること」です。いきなりこのような定義を提示されても分かりにくいと思うので、ここではとりあえず、交互作用は「状況次第」という意味だと考えてください。
状況次第とはどういうことでしょうか。そのことを理解するために、まずは交互作用の具体例を見てみます。
交互作用の例
ある会社の人事部で働いているAさんは、今後どのようなパーソナリティの人を採用すべきかを知りたいと考えています。そこで、社員が採用時にどのようなパーソナリティを持っていれば、現在のパフォーマンスが高いのかを調べることにしました。
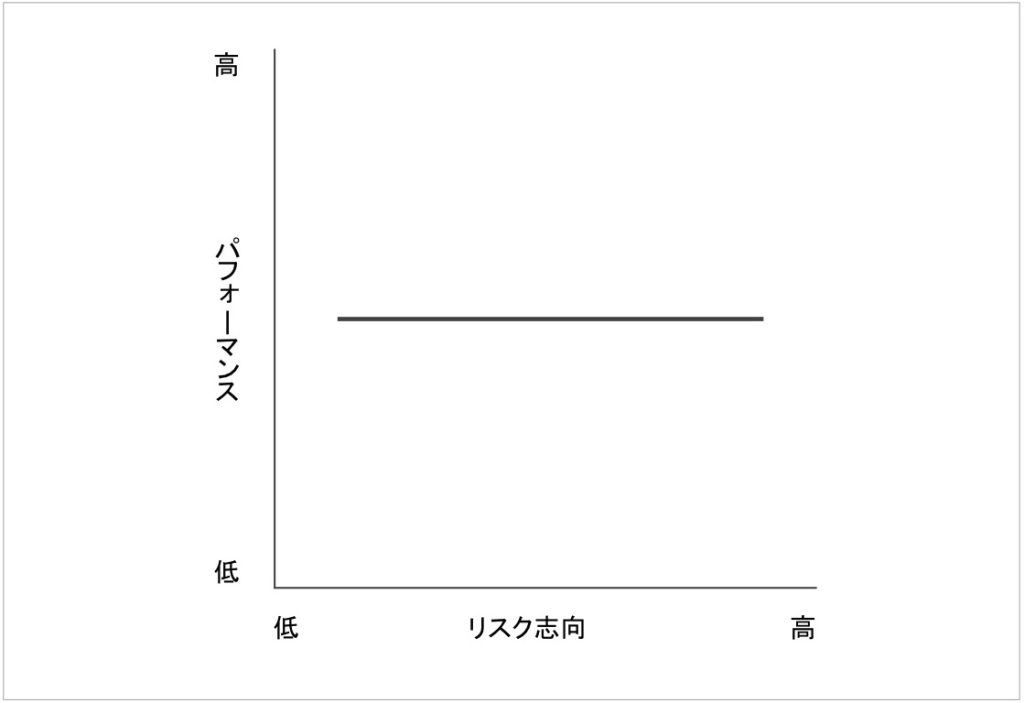
パーソナリティといっても色々ありますが、Aさんの手元には、社員の採用時のリスク志向に関するデータがあったので、それと現在のパフォーマンスとの関係を見てみました。その結果、リスク志向が高くても低くてもパフォーマンスは変わらないということが分かりました(図1)。
図1. パフォーマンスに対するリスク志向の影響
Aさんはこの結果を同じ部署のBさんに伝えました。Bさんはこの結果に疑問を抱き、リスク志向が高い方が良いか低い方が良いかは、仕事内容次第ではないのかと考えました。
そこでBさんは、社員の主な仕事内容に関するデータも使って、リスク志向とパフォーマンスの関係を見てみました。
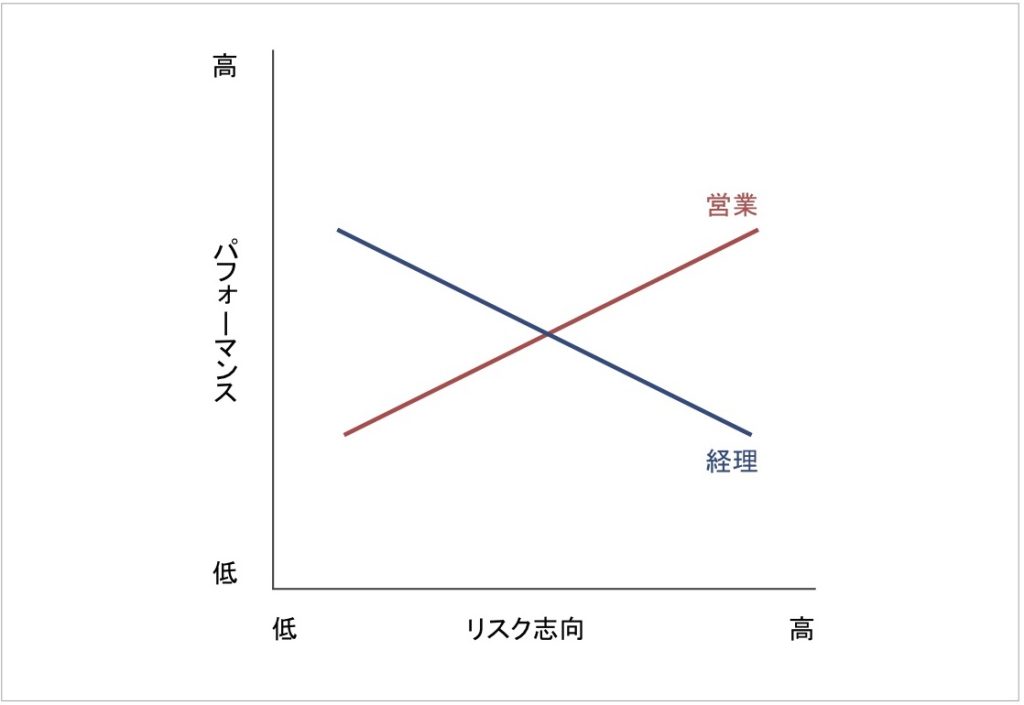
その結果、経理を担当している社員に関してはリスク志向がパフォーマンスに負の影響を与えている(リスク志向が低い方がパフォーマンスが高い)のに対して、営業を担当している社員に関してはリスク志向がパフォーマンスに正の影響を与えている(リスク志向が高い方がパフォーマンスが高い)ことが分かりました(図2)。つまり、Bさんが考えた通り、パフォーマンスに対するリスク志向の影響は、仕事内容次第でした[1]。
図2. パフォーマンスに対するリスク志向と仕事内容の影響
パフォーマンスに対するリスク志向の影響は「状況次第」、具体的には仕事内容次第でした。これを丁寧に言い換えると、「リスク志向という要因がパフォーマンスという従属変数に及ぼす影響の方向(正の影響か負の影響か)が、仕事内容という別の要因の水準(経理か営業か)によって異なった」ということになります。
冒頭で紹介した交互作用の定義を踏まえると、上の例では交互作用があったと言えます。具体的には「パフォーマンスに対するリスク志向と仕事内容の交互作用が見られた」わけです。
交互作用を検討する意義
上の例では、Aさんは交互作用を検討せず、リスク志向とパフォーマンスは関係ないという結論を導出しようとしていました。しかしBさんが交互作用を検討した結果、実はリスク志向とパフォーマンスは大いに関係しており、その関係は仕事内容次第であることが分かりました。Aさんのように交互作用を検討しないと、場合によっては重大な事実を見落としかねません。
交互作用と主効果
交互作用について何となくつかめたところで、交互作用と主効果の違いを確認します。急に主効果という新しい言葉を出してしまい恐縮ですが、交互作用を理解する上で主効果を理解することは避けられません。
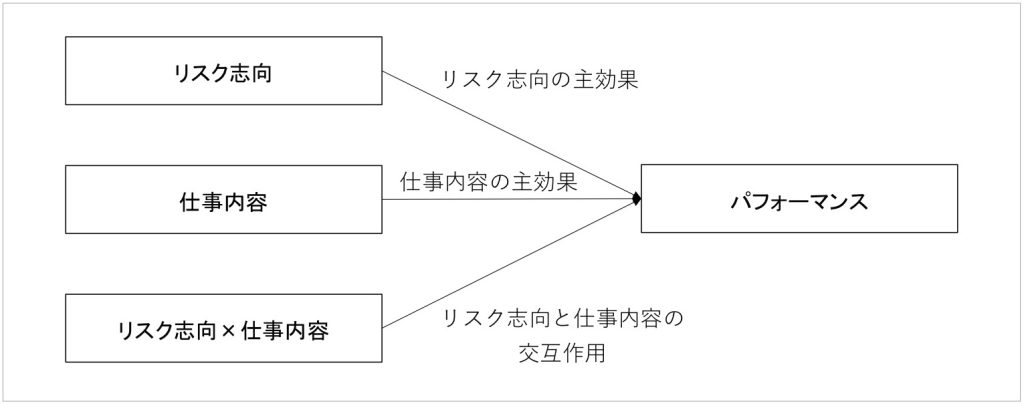
ここでもう一度、上のBさんの例に戻ります。この例では、Bさんはリスク志向と仕事内容がパフォーマンスに及ぼす影響を調べていました。実はこのときBさんが見ていた影響には3種類あります(図3)。
図3. Bさんが見ていた3種類の影響
1つ目は「リスク志向の主効果」です。これは、仕事内容と関係なくリスク志向がパフォーマンスに与える影響のことです。2つ目は「仕事内容の主効果」です。これは、リスク志向と関係なく仕事内容がパフォーマンスに与える影響のことです。
つまり主効果とは、それぞれの独立変数(今回はリスク志向と仕事内容)が独自に従属変数(今回はパフォーマンス)に与える影響を指します。
Bさんが見ていた影響の3つ目が「リスク志向と仕事内容の交互作用」(しばしば「リスク志向×仕事内容」と表記されます)です。この交互作用があるということは、「リスク志向がパフォーマンスに及ぼす影響の方向または大きさが、仕事内容の水準によって異なる」こと(つまりリスク志向がパフォーマンスに及ぼす影響は仕事内容次第であること)[2]です。
2つの主効果と1つの交互作用を検討した際に得られる結果には、様々なものがあり得ます。具体的にはどのようなものがあるのでしょうか。図4で見てみましょう。
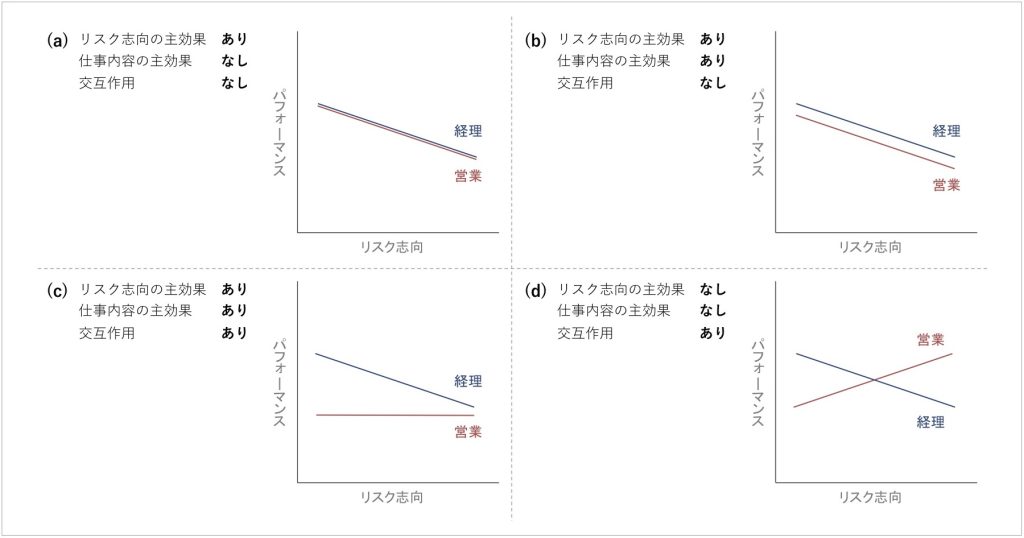
図4. 主効果と交互作用の例
図4 (a) のグラフでは、リスク志向の主効果があります。具体的には、リスク志向が低い方がパフォーマンスが高くなっています。しかし、仕事内容の主効果はありません。つまり、仕事内容が経理であっても営業であってもパフォーマンスは変わらないということです。リスク志向と仕事内容の交互作用もありません。リスク志向がパフォーマンスに及ぼす影響が仕事内容によって変わらないということです。
図4 (b) のグラフでは、リスク志向の主効果と仕事内容の主効果があります。具体的には、リスク志向が低い方がパフォーマンスが高くなっています。また、仕事内容が経理の方がパフォーマンスが高くなっています。リスク志向と仕事内容の交互作用はありません。つまり、リスク志向がパフォーマンスに及ぼす影響が仕事内容によって変わらないということです。
図4 (c) のグラフでは、リスク志向の主効果と仕事内容の主効果があります。図4 (b) と同様、全体的に、リスク志向が低い方がパフォーマンスが高くなっています。また、仕事内容が経理の方がパフォーマンスが高くなっています。図4 (b) との大きな違いは、リスク志向と仕事内容の交互作用がある点です。これは「リスク志向がパフォーマンスに及ぼす影響の方向または大きさが、仕事内容の水準によって異なる」こと(リスク志向がパフォーマンスに及ぼす影響は仕事内容次第であること)を意味しています。
「仕事内容次第」とは具体的にどういうことでしょうか。図4 (c) のグラフを見ると、仕事内容が経理のとき、リスク志向はパフォーマンスに負の影響を与えているけれど、仕事内容が営業のとき、リスク志向はパフォーマンスに影響を与えていないことが分かります。
図4 (d) のグラフは上のBさんの例のグラフ(図2)と同じものです。ここではリスク志向の主効果と仕事内容の主効果がありません。要するに、リスク志向や仕事内容は独自にはパフォーマンスに影響を与えていません。その一方で、リスク志向と仕事内容の交互作用はあります。
図4 (d) のグラフを見ると、仕事内容が経理のとき、リスク志向はパフォーマンスに負の影響を与えているのに対して、仕事内容が営業のとき、リスク志向はパフォーマンスに正の影響を与えていることが分かります。
交互作用の有無を判断する際、もちろん統計的検定を行わなければいけないのですが(詳細は下の分散分析や重回帰分析に関するセクションを参照してください)、グラフの形を見るだけでもおおよその見当をつけることができます。
図4 (a) と図4 (b) のように、グラフ内の2本の線が平行である場合、交互作用はないと考えられます。その一方で図4 (c) と図4 (d) のように、グラフ内の2本の線が平行でない場合、交互作用がある可能性があります。
様々な交互作用
交互作用があると一言でいっても、バリエーションがあります。
図5. 様々な交互作用の例
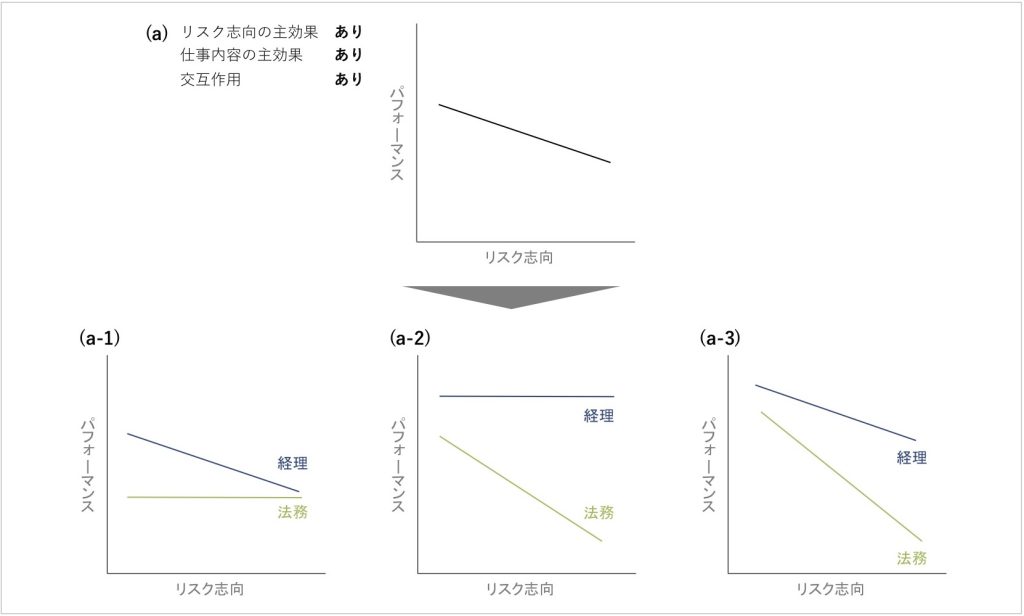
ここでは先ほどと別の例として、経理と法務におけるリスク志向とパフォーマンスの関連を考えてみます。図5の(a)は、仕事内容の影響を考慮する前のグラフです。このグラフにおいて考えられるリスク志向と仕事内容の交互作用のバリエーションを、図5の (a-1) から (a-3) で表しています。
図5の (a-1) から (a-3) はいずれも、リスク志向の主効果も、仕事内容の主効果も、リスク志向と仕事内容の交互作用もある場合を表しています。
どのグラフにおいても、リスク志向が低い方がパフォーマンスが高くなっています。また、仕事内容が経理の方がパフォーマンスが高くなっています。しかし3つのグラフの形は大きく異なっています。これは、交互作用の中身がグラフによって異なるからです。
図5 (a-1) は図4 (c) と同じパターンです。仕事内容が経理のとき、リスク志向はパフォーマンスに負の影響を与えている一方で、仕事内容が法務のとき、リスク志向はパフォーマンスに影響を与えていません。
それに対して、図5 (a-2) のグラフでは、仕事内容が経理のとき、リスク志向はパフォーマンスに影響を与えておらず、仕事内容が法務のとき、リスク志向はパフォーマンスに負の影響を与えています。
図5 (a-3) のグラフでは、仕事内容が経理か法務かにかかわらず、リスク志向はパフォーマンスに負の影響を与えていますが、特に法務の方でその影響が強く、リスク志向の上昇に応じてパフォーマンスがより大きく低下しています。このように、独立変数が従属変数に及ぼす影響が同じ方向であってもその影響の大きさがグループごとに異なる場合も、交互作用があるとみなされます。
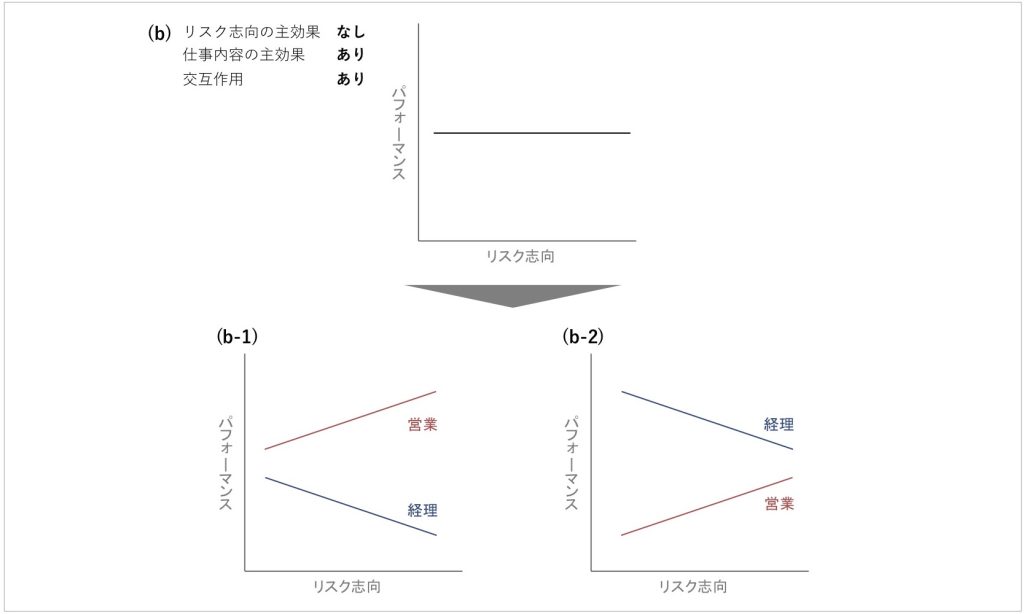
他の例も見てみましょう。図6の (b) はリスク志向とパフォーマンスの関連を示したグラフです。これは仕事内容の影響を考慮する前のものです。このグラフにおいて考えられるリスク志向と仕事内容の交互作用のバリエーションを、図6の (b-1) と (b-2) で表しています。
図6 の (b-1) も (b-2) も、リスク志向の主効果はなく、仕事内容の主効果およびリスク志向と仕事内容の交互作用はあります。
図6. 様々な交互作用の例
図6の (b-1) と (b-2) では、営業と経理で全体的にどちらのパフォーマンスが高いかという仕事内容の主効果に違いはありますが、交互作用の中身は同じです。具体的には、仕事内容が経理のとき、リスク志向はパフォーマンスに負の影響を与えており、仕事内容が営業のとき、リスク志向はパフォーマンスに正の影響を与えています。
図5を用いて確認した通り、リスク志向と仕事内容の交互作用があるといっても、それは「リスク志向がパフォーマンスに及ぼす影響の方向または大きさが、仕事内容の水準によって異なる」ことしか意味していません。仕事内容によってリスク志向の影響の方向がどう異なるのか、リスク志向の影響の大きさがどう異なるのかまで分からないと、交互作用の中身まで把握したことにはなりません。
また、図6を用いて確認した通り、たとえ交互作用の中身を把握しても、主効果を把握していないと、独立変数と従属変数の関連はつかみきれません。
分析をする際には、それぞれの独立変数の主効果、独立変数間の交互作用、さらには、交互作用の中身を確認しましょう。
分散分析における交互作用
自分で交互作用があるかどうかを検討したい場合は、どうすれば良いのでしょうか。主には、分散分析や重回帰分析などの分析方法を用います。ここではそれぞれの分析方法について紹介します。
分散分析を行う場合は、二要因分散分析を行うことになります(一要因分散分析では交互作用は検討できません)。
ここでは30人分のデータを用いて、リスク志向と仕事内容がパフォーマンスに与える影響を検討するとします。このとき、独立変数にはカテゴリカル変数2つ(リスク志向 [高・低] と仕事内容 [経理・営業])を投入し、従属変数には連続変数(パフォーマンス)を投入します。
その結果、例えば図2と表1が統計ソフトから出力されたとします。図2を見る限りだと、リスク志向と仕事内容の主効果はなさそうですが、リスク志向と仕事内容の交互作用はありそうです。
ここで「なさそう」や「ありそう」といった曖昧な言葉を使っているのは、グラフを見るだけでは本当のところどうかは判断できないためです。そこで表1を見ます。
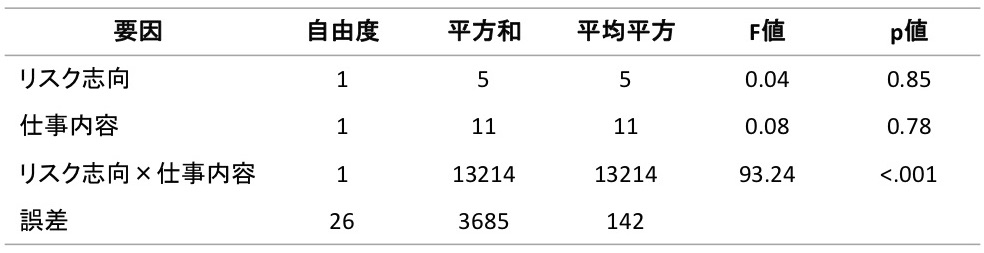
表1. 分散分析の結果
表1は分散分析表というものです。色々難しい言葉が登場しているので、それぞれを簡単に紹介します。
「自由度」は水準数やデータ数を反映しています。リスク志向の自由度は、リスク志向の水準数(高・低の2つ)から1を引いたもの(2 – 1 = 1)です。仕事内容の自由度は、仕事内容の水準数(経理・営業の2つ)から1を引いたもの(2 – 1 = 1)です。リスク志向×仕事内容の自由度は、リスク志向の自由度と仕事内容の自由度を掛け合わせたもの(1×1 = 1)です。誤差の自由度は、全データ数(今回は30人分)から、リスク志向の自由度と、仕事内容の自由度と、リスク志向×仕事内容の自由度と、1を引いたもの(30 – 1 – 1 – 1 – 1 = 26)です。
「平方和」はある要因で説明できるデータのばらつきの程度を指します。例えばリスク志向の平方和は、リスク志向で説明できるパフォーマンスのばらつきの程度(今回は5)です。これが誤差の平方和、つまり誤差で説明できてしまうばらつきの程度(今回は3685)を十分に上回れば、リスク志向が原因でパフォーマンスにばらつきが生じたとみなせます。
今回はリスク志向の平方和は誤差の平方和をまったく上回っていないので、リスク志向が原因でパフォーマンスにばらつきが生じたとは考えにくい、つまりパフォーマンスに対するリスク志向の主効果はなさそうです。
「平均平方」は平方和を自由度で割った値で、「F値」は平均平方をもとに算出される値です。F値が大きいほどある要因の影響が大きいことになります。
例えばリスク志向のF値(0.04)はあまり大きくないので、リスク志向の主効果はあまり大きくなさそうです。実際にp値(0.85)を見てみると、リスク志向の主効果は有意でないと判断できます(有意水準が5%の場合)[3]。リスク志向と同様に、仕事内容の主効果も有意ではないことが分かります。その一方で、リスク志向と仕事内容の交互作用は有意です[4]。
交互作用が有意だった場合、分析をそのまま終わらせるわけにはいきません。図5で見た通り、交互作用があることだけが分かっても、具体的にどのような交互作用があるのかまでは分からないためです。
そこで、単純主効果検定という検定を行い、具体的にはどのような交互作用があるのかを明らかにします。単純主効果検定では、リスク志向がパフォーマンスに与える影響(具体的には上で紹介した平方和やF値やp値)を、仕事内容が経理の場合と営業の場合で分けて見ることができます。
今回の単純主効果検定の結果、仕事内容が経理の場合は、リスク志向はパフォーマンスに有意な負の影響を与えている一方で、仕事内容が営業の場合は、リスク志向はパフォーマンスに有意な正の影響を与えていることが分かりました。
重回帰分析における交互作用
交互作用を検討するため、同じ30人分のデータを用いて今度は重回帰分析を行ってみます。分散分析では独立変数はカテゴリカル変数でなければいけませんでしたが、重回帰分析では独立変数はカテゴリカル変数であっても連続変数であっても構いません。
そこで今回は、独立変数に連続変数(リスク志向)とカテゴリカル変数(仕事内容 [経理・営業])、従属変数に連続変数(パフォーマンス)を投入します。その結果、例えば表2が統計ソフトから出力されたとします。
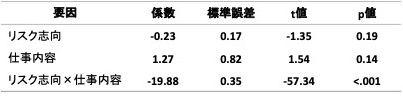
表2. 重回帰分析の結果
「係数」は、ある要因の単位が1増えたときに、従属変数がどのくらい増えるかを示した値です。ある要因の係数が正の値であれば、その要因は従属変数に正の影響を与えている可能性があります。また、ある要因の係数の絶対値が大きければ、その要因は従属変数に大きい影響を与えている可能性があります。
例えば、リスク志向の係数(-0.23)は負の値を取っていますので、リスク志向はパフォーマンスに負の影響を与えていそうです。ただし係数の絶対値は比較的小さいので、リスク志向がパフォーマンスに与えている影響はあったとしてもごくわずかでしょう。
「標準誤差」は、今回得られた係数(今回用いた30人分のデータから得られた値)が母集団から得られるはずの係数(仮に全社員からデータを取った場合に得られる値)をどれほど正確に推測しているかを表しています。この値が小さいほど正確に推測していることになります。
「t値」は係数や標準誤差をもとに計算されます。上で紹介したF値のように、t値が大きいほど、ある要因の効果が大きいということになります[5]。
例えば、リスク志向のt値(–1.35)はあまり大きくないので、リスク志向の主効果はあまり大きくなさそうです。p値(0.19)を見てみると、リスク志向の主効果は有意ではありません(有意水準が5%の場合)。同様に、仕事内容の主効果も有意ではありません。その一方で、リスク志向と仕事内容の交互作用は有意です[6]。
分散分析を行ったときと同様に、交互作用が有意だった場合は、さらに詳細な分析が必要です。ここでも単純主効果検定という検定を行い、具体的にはどのような交互作用があるのかを明らかにします。
繰り返しになりますが、単純主効果検定を行うと、リスク志向がパフォーマンスに与える影響(具体的には上で紹介した係数やt値やp値)を、仕事内容が経理の場合と営業の場合で分けて見ることができます。
今回も単純主効果検定の結果、仕事内容が経理の場合は、リスク志向はパフォーマンスに有意な負の影響を与えている一方で、仕事内容が営業の場合は、リスク志向はパフォーマンスに有意な正の影響を与えていることが分かりました。
おわりに
交互作用は身近にあふれており、交互作用を意識するだけで様々な場面に対する見方は変わります。今回はリスク志向がパフォーマンスに与える影響に関する例を用いて交互作用を説明しましたが、他にも交互作用の例はいくらでも考えられます。
例えば、対面とオンラインのどちらで1 on 1ミーティングを行った方が部下のモチベーションが上がるかが気になったとします。このとき、もしかするとチームの大きさが関わっているかもしれません。大きいチームでは対面で行った方が部下のモチベーションが上がるのに対して、小さいチームでは対面でもオンラインでも部下のモチベーションの上がる程度は変わらないかもしれません。
例えば、天気が各店舗の売り上げにどのくらい影響するのかを明らかにしたいとします。ここでは、もしかすると駅から店舗までの距離が関わっているかもしれません。駅から遠い店舗では雨の日に売り上げが大きく下がるのに対して、駅から近い店舗は逆に雨の日に売り上げがやや上がるかもしれません。
こういったことは、交互作用を検討しなければ分からないことです。本コラムをきっかけに、今までは気づかなかった交互作用を見つけて、実践に活かしていただければ幸いです。
参考文献
山田 剛史・村井 潤一郎 (2015). やわらかアカデミズム・<わかる>シリーズ よくわかる心理統計 ミネルヴァ書房
脚注
[1] ここで挙げている例は、あくまで架空の話です。分析結果の内容そのものを実務的に役立てることはできません。ご注意ください。
[2] 「リスク志向と仕事内容の交互作用」を具体的に言い換えると、二通りの言い方ができます。1つは「リスク志向がパフォーマンスに及ぼす影響の方向または大きさが、仕事内容の水準によって異なる」こと(つまりリスク志向がパフォーマンスに及ぼす影響は仕事内容次第であること)です。もう1つは「仕事内容がパフォーマンスに及ぼす影響の方向または大きさが、リスク志向の水準によって異なる」こと(つまり仕事内容がパフォーマンスに及ぼす影響はリスク志向次第であること)です。リスク志向がパフォーマンスに与える影響の方に関心があるのであれば、前者の言い方をすることになり、仕事内容がパフォーマンスに与える影響の方に関心があるのであれば、後者の言い方をすることになります。本コラムでは前者の言い方をしています。なぜなら、本コラムで用いている例において、もともとAさんはパーソナリティ(リスク志向)がパフォーマンスに与える影響に関心を持っていたためです。ちなみに、前者の言い方では、リスク志向を独立変数、仕事内容を調整変数と捉えており、後者の言い方では逆に、仕事内容を独立変数、リスク志向を調整変数と捉えています。
[3] 有意という語句に関しては過去のコラムを参照してください。
[4] この検定結果を学術的に報告する際には、「リスク志向の主効果(F (1, 26) = 0.04, p = .85)および仕事内容の主効果(F (1, 26) = 0.08, p = .78)は有意ではなかったが、リスク志向と仕事内容の交互作用(F (1, 26) = 93.24, p < .001)は有意であった」というように、F値とp値を報告します。Fに続く括弧の中に「1, 26」という数字がありますが、これは各要因の自由度と誤差の自由度を表しています。
[5] t値は効果の大きさに応じて大きくなりますが、サンプルサイズが増加してもそれに応じて大きくなるため、厳密には、要因の効果の大きさを表すものではありません。ここでは、話をシンプルにするため、このように記述しています。
[6] 重回帰分析の結果を学術的に報告する際には、「リスク志向の主効果(b = –0.23, p = .19)および仕事内容の主効果(b = 1.27, p = .14)は有意ではなかったが、リスク志向と仕事内容の交互作用(b = –19.88, p < .001)は有意であった」といった形で報告するのが一般的です。
執筆者
 ターン 有加里ジェシカ
ターン 有加里ジェシカ
一橋大学商学部経営学科を卒業後、東京大学大学院人文社会系研究科の修士課程を修了。修士課程在学中、日本社会心理学会の若手研究者奨励賞などを受賞。現在は日本学術振興会の特別研究員(DC1)として、東京大学大学院人文社会系研究科の博士後期課程に在籍。主な研究テーマは、人々が所属集団のために行動する心的メカニズムであり、実験や調査など様々な手法を組み合わせて検討を行っている。その成果として執筆した論文は、『心理学研究』や『Personality and Individual Differences』などの学術雑誌に掲載されている。