ある会社が「社内で実施した２種類の研修は、従業員のコンプライアンス意識に効果があるのか調べたい」と考え、研修効果の検討を行いました。効果の比較に際しては、専門家のコメントを参考にして、A研修・B研修に加えて、敢えて研修をしないグループも構成し、A研修を受けたグループ、B研修を受けたグループ、研修を受けていないグループの３条件を設定しました。

研修実施後に従業員のコンプライアンス意識に関するアンケートを行い、その集計結果を以下の図に示しました。なお、コンプライアンス意識のアンケートは、１（まったく意識していない）～３（どちらともいえない）～５（強く意識している）で測定された数値を表しています。

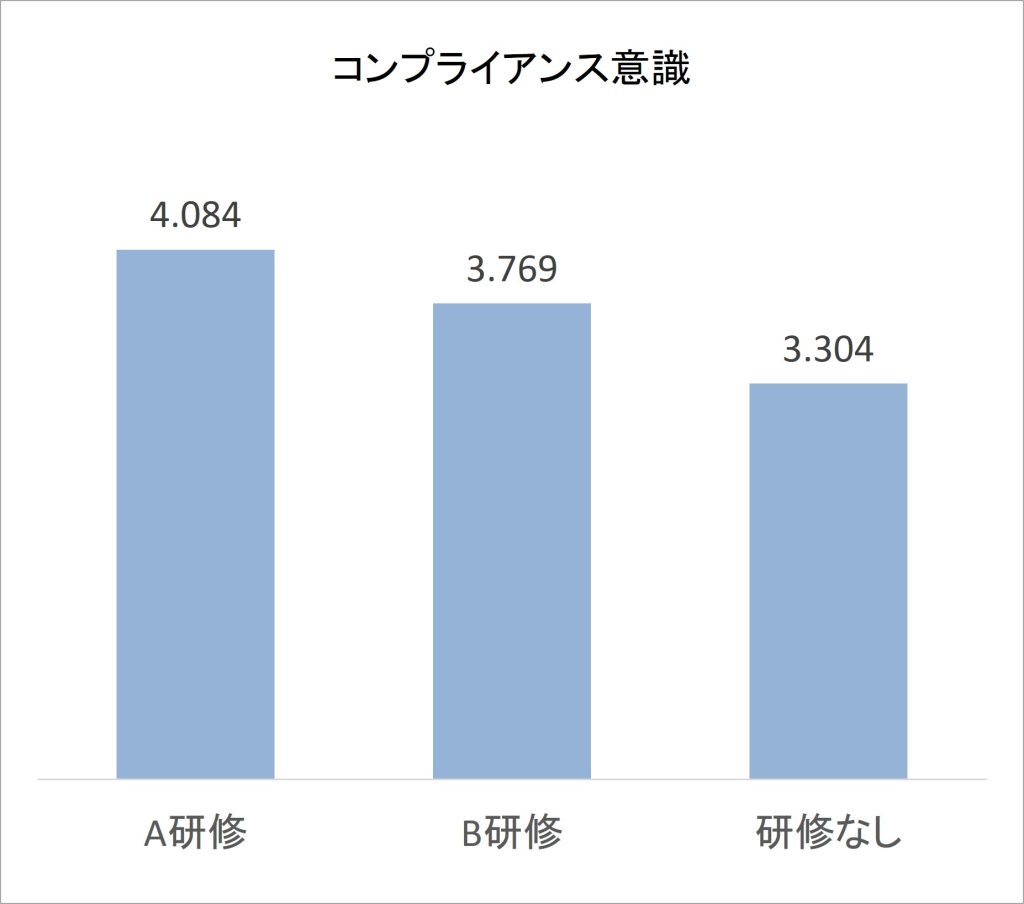
図１　研修参加によるコンプライアンス意識の高さの比較（架空データ）

集計結果を見ると、コンプライアンス意識の得点はA研修で4.1と最も高く、次いでB研修3.8、研修を受けなかったグループは3.3と低くなっています。この結果から、「A研修とB研修はいずれも効果があった。A研修の得点がもっとも高いから、A研修を中心にしつつ、B研修も実施する企画を進めよう」と考えられるかもしれません。

さて、このデータの読み取り方で、本当に問題ないのでしょうか。このような、「複数のグループ間の平均得点の比較」について、本コラムでは「分散分析」と呼ばれる手法を解説します[1]。

３つ以上のグループの得点を比較する問題点

研修によってコンプライアンス意識に高まりが生じたかを検証するためには、「各グループの間でコンプライアンス意識の高さには違いがある」ことを検討すれば良いことになります。

その検討方法の一つとして、「２つのグループ間の平均値の差を統計学的に検証するデータ分析（t検定）を、A研修/B研修、A研修/研修なし、B研修/研修なしのグループ間で３回実施する」ことが考えられるかもしれません。

しかし、この方法は問題があります。統計学的検定の手続きでは、「取得したデータから得られた結果は、帰無仮説を前提としたときにどのくらいの確率で生じると推定されるか[2]」をｐ値として算出して、判断を行います。

この方法に対して、同じような分析を何度も実施するやり方は、偶然に有意な結果が得られる可能性を高めることになります。「下手な鉄砲も数打てば当たる」というように、試行回数を増やせば偶然のヒットが出てしまうということです。

つまり、統計学的検証を複数回実施することは、偶然にも有意な結果が出てしまう可能性を高める問題を持っており、これを「多重検定の問題」と呼びます。比較するグループが３つ以上になると、この問題に対処した分析方法が求められることになるのです。

分散分析とは何か

「３つ以上のグループ間で平均値の差を比較検討する」場面で最もよく用いられる分析方法が、分散分析（ANOVA: ANalysis Of VAriance）です。分散分析は、検証したい成果指標におけるデータのばらつき（分散）に着目した分析であり、その分析プロセスの中に、多重検定の問題に対処した処理を含んでいることが特徴です。

最初に、分散分析で扱われる「分散」とは何かを説明していきます。そして、グループ間の得点差の存在を検証するにあたって、分散に着目することでグループ間の平均値の差が検証できる仕組みについて解説していきます。

分散とは何か

分散とは、ある指標について取得したデータが、その平均値に対してどの程度ばらついているかを表す指標です。取得したデータにおける分散の計算式は以下のようになっています。

図２　分散の計算式

計算式に示されている通り、分散とは、偏差平方和をデータに含まれる回答者の人数で割り算したものです。

分散の式に含まれる偏差平方和について、偏差とは「ある指標における、各データと全体平均の差」を表します。例えば、あるテストの平均点を60点としたとき、80点を取った人の偏差は80-60＝+20点、30点を取った人の偏差は30-60＝-30点になります。

分散は「平均に対して、データがどの程度ばらついているか」ですから、各データが平均から大きく離れているほど分散が大きくなるよう計算される必要があります。そのため、分散の計算式では、まず偏差を算出し、「各データが平均からどれだけ離れているか数値化する」ことから始まります。

次に、全体平均から各データがどれだけ離れているかを表す、偏差の値を集約していきます。それにより、各データで見た平均とのズレを統合して「全体的に、データが平均からどの程度離れているか（＝ばらついているか）」を表現することを考えていきたいのですが、ここで問題が生じます。

それは、テストの得点例でもそうなっているように、偏差は正の値と負の値の両方を取ることです。そのせいで、偏差をそのまま合計していき「各データが平均から離れている程度の統合」をしようとすると、プラスとマイナスで偏差同士が打ち消しあってしまい、計算がおかしくなってしまうのです。

そこで分散の計算では、この正負の打ち消しあい問題を解消するため、算出した偏差を二乗（平方）することで対処しています。二乗することで偏差の値がすべてプラスとなるため、それを合計した数値が「各データが平均から離れている程度を集約したもの」を表せるようになるのです。

以上の計算の展開を整理すると、各データが平均からどの程度離れているかを算出し（偏差）、その値を二乗（平方）した上で、合計する（和）計算処理をしています。分散の式における「偏差平方和」は、これらの計算処理をまとめた名称です。

そして、分散の計算式では、「偏差平方和を、回答者の人数で割り算して調整する」方法をとっています。

偏差平方和は各データで算出される偏差を二乗して合計したものであるため、回答者の人数が増えると、それに比例して偏差平方和も大きくなってしまいます。そこで、回答者の人数に比例して値が大きくなるならば、回答者の人数で割り算すればよいという発想で、この問題に対処したものが、分散の計算式となっています。

以上のプロセスを経て、分散の計算式は「偏差平方和を回答者の人数で割り算したもの」となるのです。この計算過程を知ることで、分散が「取得したデータが、その平均に対してどの程度ばらついているか」を表す指標であることが、よりはっきりと理解できるでしょう。

分散の計算式がわかったところで、分散が大きい場合（左）と小さい場合（右）の得点分布を次の図で示してみます。

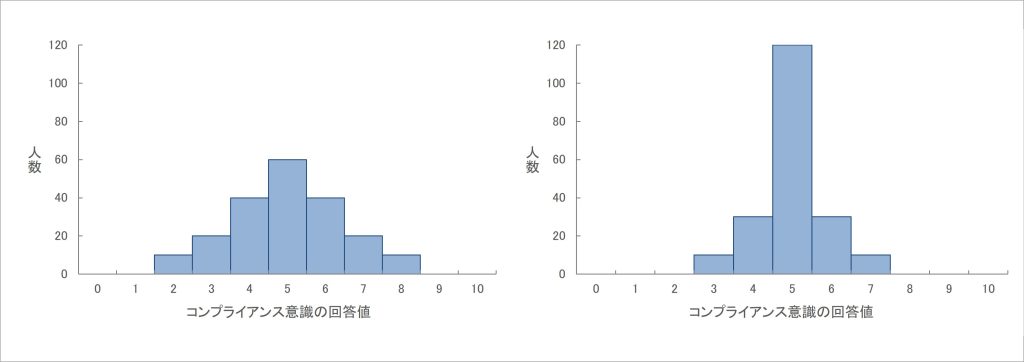
図３　分散が大きい/小さいデータのそれぞれの得点分布例

図３を見ると、分散が大きい左側の回答値の得点分布では、平均５点に対して、平均付近に回答が集中しつつも、２～３点や７～８点といった平均から離れた回答がいくらか存在しています。

他方、分散が小さい右側の得点分布では、ほとんどの回答が平均５点付近に存在し、そこから離れた値もほとんどない状態になっています。

分散の計算式からもわかるように、分散の大きさは得点分布によく反映されるものになっているわけです。

グループ間の得点差の有無が、分散に着目してわかるメカニズム

ここまで、分散そのものの仕組みや、それが得点分布においてどのように表れるかを追いました。しかし、分散が意味することは平均に対するデータのばらつきの程度であり、得点差そのものではありません。

それでは、なぜ分散分析はグループ間の得点差を検証するに際して、分散に着目するのでしょうか。それは、「ある指標のデータのばらつきを説明する要因は、その指標における得点の違いを生み出す要因にもなっているから」です。

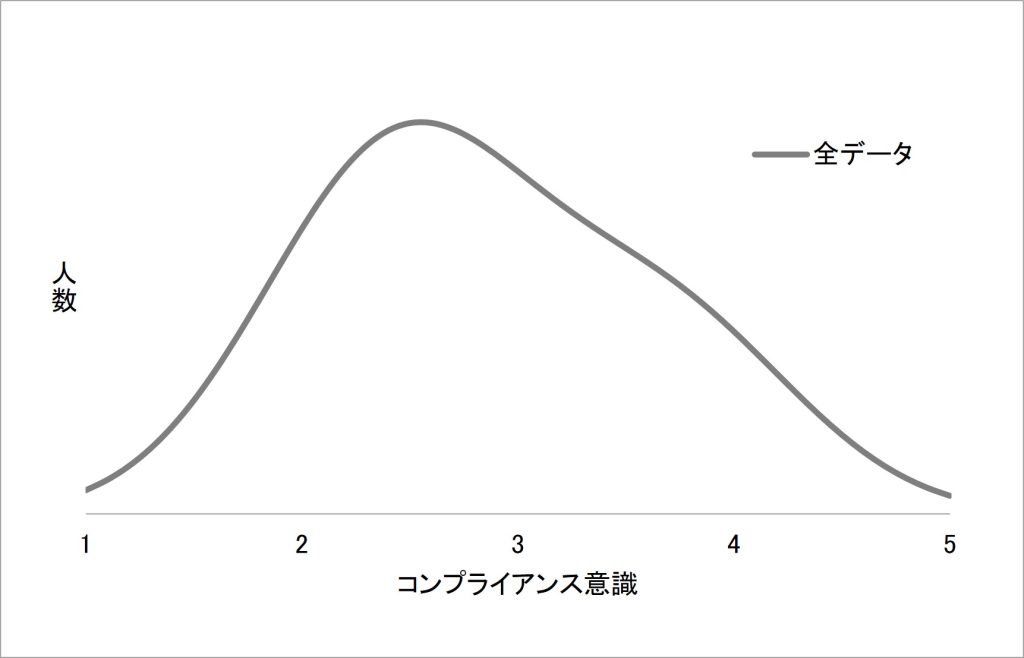
例えば、従業員のコンプライアンス意識についてアンケート調査を行った結果、以下のような回答値の分布が得られたとします。平均は約2.9点であり、データは平均に対してかなりばらつきがある、つまり分散がある状態です。

図４　コンプライアンス意識のアンケート調査の得点分布

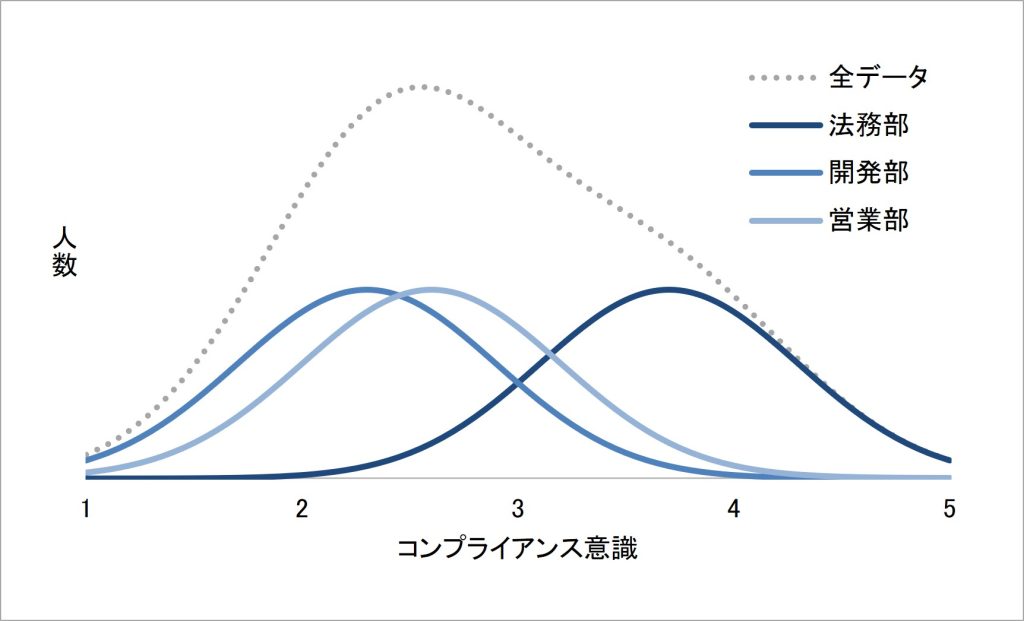
このような、コンプライアンス意識の得点に分散があるデータについて、法務部・開発部・営業部それぞれの回答分布の情報を重ねてみたら、以下の図のようになったとします。

図５　コンプライアンス意識のアンケート調査 3部署それぞれの得点分布

３部署それぞれの得点分布をみると、法務部はコンプライアンス意識の得点が平均より高い得点範囲に分布しており、逆に営業部・開発部は平均より低い得点範囲に分布しています。

このことから「全データにおいてコンプライアンス得点の分散があったのは、３部署の違いによって現れた得点の高低により、データにばらつきができたからだ」と考えることができます。このように、ある指標のデータのばらつきを説明する要因は、その指標の得点の高低を説明する要因にもなっています。

まとめると、データに分散があることは、平均から離れた高い/低い得点が存在することと対応するため、データの分散を説明する要因は、その得点の高低を説明する要因にもなるわけです。

この発想に基づいて、関心のある成果指標について、そのデータのばらつき（分散）を説明する要因を分析によって検証するのが、分散分析となります。

分散分析の計算内容

分散分析では、成果指標に関するデータのばらつきについて計算を進めていき、着目したグループの違いが、そのばらつきを説明する要因といえるか否か検討します。

ここからは、その具体的な計算内容について紹介をしていきます[3]。ここでは、コンプライアンス意識の得点に関してA研修・B研修・研修なしの３グループを比較することを考えます[4]。

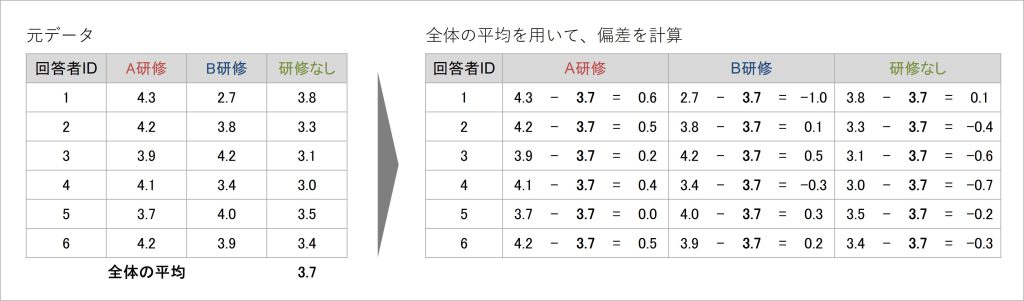
図６　分散分析の計算プロセス（１）

分散分析では、先に紹介した分散の計算式を少し応用した手法で、データのばらつきを計算していきます。しかし、その根本にある発想は、基本となる分散の計算式と同じです。すなわち、様々な偏差を計算していき、それを二乗して合計した「偏差平方和」を、応用的なデータ数の指標（自由度）で割り算する手続きを進めていきます。

最初に、各回答者のデータが全体の平均からどの程度ずれているか、各データの得点から全体平均を引き算して算出します。これは、分散の計算における偏差の計算と同じです。この計算により、「各データが持つばらつき（分散）要素を偏差として抽出した」イメージになります。

ここからが、分散分析における応用的な計算部分です。分散分析では、ある要因が成果指標の分散を説明できるか検証するために、「着目した要因が、成果指標のデータのばらつき（分散）をどの程度生み出したのか」を直接計算していきます。

それに向けて、成果指標における分散を、「着目した要因によって生み出された分散」と「それ以外の要因によって生み出された分散」に切り分ける計算を進めていきます。

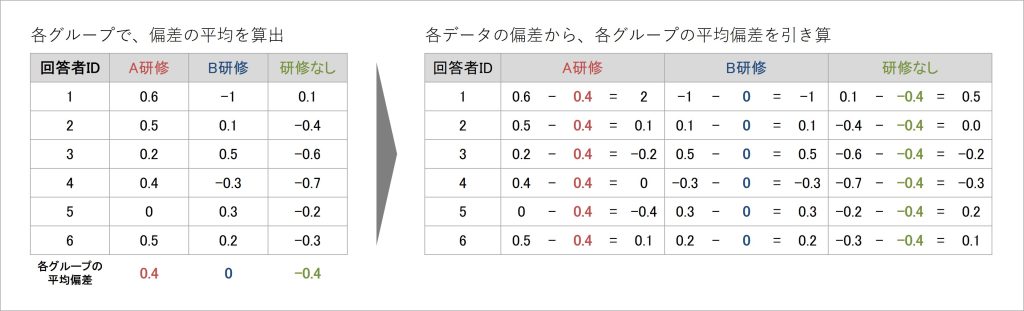
具体的には、次の計算で、着目した要因（グループの違い）ごとに、偏差の平均を算出していきます。例のデータでは、コンプライアンス意識得点について、研修参加の様相（A研修・B研修・研修なし）それぞれで平均偏差を算出しています。

図７　分散分析の計算プロセス（２）

偏差は「各得点が平均からどの程度離れているか」ですが、各データが持つばらつき（分散）の要素としてイメージしていました。そして、各グループにおける平均的な偏差は「あるグループに所属することによって、得点が平均からどの程度離れるのか」を表します。

したがって、各グループの平均的な偏差は「あるグループに所属することで生み出される分散の要素」だと考えられます。このようにして、成果指標の分散に対して、各グループに所属することが生み出す分散の程度を計算していくわけです。

さらに、各データの偏差から、グループごとに計算した平均偏差を引き算した値を算出します。各データの偏差は「成果指標全体の得点のばらつき（分散）の要素」のイメージでした。そこからグループごとの平均偏差、つまり「グループによって生み出される分散の要素」を引き算しているため、その値は「グループの違いによって説明されない、成果指標の分散の要素」と考えられます。

例のデータの内容で言い換えれば、「研修参加の様相（A研修・B研修・研修なし）によって生まれたコンプライアンス意識得点の分散要素」と、「研修参加の様相では説明されない、コンプライアンス意識得点の分散要素[5]」が、それぞれ偏差として算出されたことになります。

このように、「全体データにおける分散」を、「グループの違いによって生み出される分散の要素」と「グループの違いによって説明されない分散の要素」に分解することが、分散分析の計算のポイントです。

以降は、分析の計算式の発想に従い計算を進めていきます。

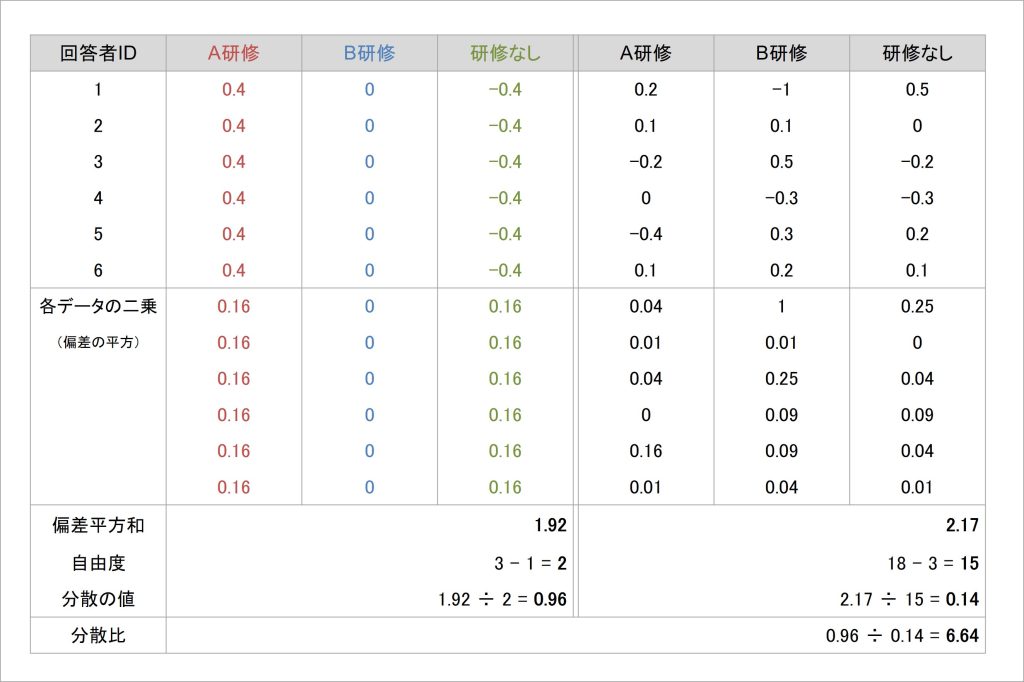
図８　分散分析の計算プロセス（３）

分散の計算式では、偏差を二乗して合計する偏差平方和を算出していました。分散分析でも同様の発想で、偏差平方和を計算していきます。

ここまでの計算で、「グループの違いによって生み出される分散の要素」と「グループの違いによって説明されない分散の要素」に分解してそれぞれ偏差を求めました。それに応じて、偏差平方和も２つ算出することになります。

なお、グループの違いによって生み出される分散の要素では、「そのグループに所属しているメンバー全員に、同様のデータのばらつきが生じる」と考えられるため、偏差平方和を算出する際の各データの偏差は、グループごとに算出された平均偏差が入ります。

もちろん、グループの違いで説明されない各データの偏差には、前に算出した「全体の偏差から、各グループの平均偏差を引き算した値」が入ります。

このようにして、「グループの違いによって生み出される分散の要素」と「グループの違いによって説明されない分散の要素」それぞれの偏差を算出し、すべての偏差を二乗してそれぞれ合計し、２つの偏差平方和を算出していきます。

そして、分散計算と同様に、偏差平方和を回答者の人数に該当するデータで割り算していきますが、ここにも分散分析ならではの特徴があります。分散分析では、分散を算出するために偏差平方和を割り算する際、「自由度」と呼ばれる指標で割り算を行います。

分散分析における自由度とは、母集団における分散の値を推定するために調整された割り算の数値のことです[6]。

分散分析は統計学的検定の手法であり、取得したデータから推測される母集団にて存在するグループ間の得点差に関心があります。そのため、取得したデータから算出された分散の値をそのまま使うことはできず、母集団の推定に用いる値として、多少の制約を含め調整された値を用いることになるのです。

グループの違いによる分散要素の自由度は「グループの個数－１」、グループの違いによって説明されない分散要素の自由度は「全回答者の人数－グループの個数」でそれぞれ求められます[7]。

例のデータでいえば、研修参加の様相による分散の要素では、グループがA研修・B研修・研修なしの３つです。単純な分散の計算方法ならば偏差平方和を３で割り算すればよいはずですが、実際に割り算に用いる値（自由度）は、３－１＝２となります。

同様に、研修参加の様相で説明されない分散の要素では、全回答者の人数が18人います。通常の分散計算であれば偏差平方和を18で割り算すればよいはずですが、割り算に用いる自由度は18－3＝15となります[8]。

以上の計算により、偏差平方和とそれを割り算する自由度が定まったため、ふたつの分散要素において具体的に分散の値が計算できるようになります。

統計学的検定　分散比に対するF検定

ここまでの計算プロセスを経て、ようやく分散分析に用いる分散の値が計算されました。分散分析では、算出した２つの分散の値の比率である「分散比」を計算します。

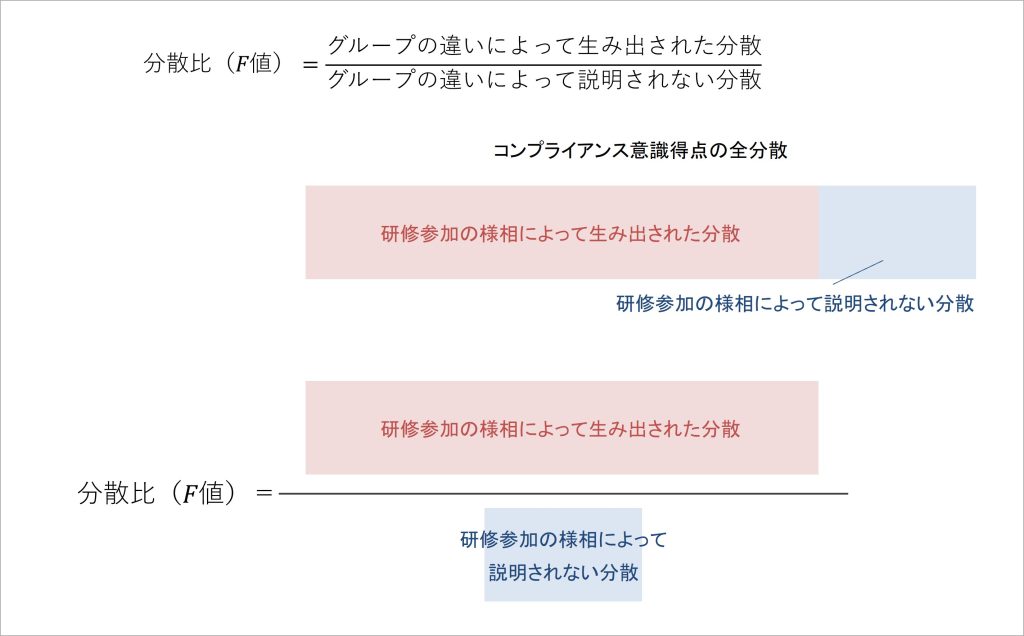
分散比は、「グループの違いによって生み出された分散」÷「グループの違いによって説明されない分散」で計算されます。この分散比の意味を図で表すと、以下のようになります。

図９　分散比のイメージ

分散比が計算しているのは、「着目した要因によって生み出された成果指標の分散は、その要因によって説明されない分散に対して、何倍の大きさなのか」です。この分散比の値が大きいほど、着目した要因によって生み出された分散が大きいことを意味します。

そして、ある指標のデータのばらつきを説明する要因は、その指標の得点の高低を説明する要因にもなっていました。これを踏まえると、ある指標の分散に対して分散比が大きいと判断された要因は、その指標の得点の高低を説明する要因だと見なすことができるわけです。

分散分析において分散の比率を算出する理由は、分散比がF分布と呼ばれる理論分布に従うことがわかっているからです。統計学的検定では、帰無仮説を前提として、取得したデータがどの程度の確率で得られるかを計算し、検証結果を判断します。分散分析も統計学的検定にあたり、それを行える指標が分散比というわけです。

そして、F分布を用いて行う統計学的検定をF検定と呼びます。F検定では、帰無仮説として「グループの違いによって生み出された（成果指標の）分散は０である」と設定[9]した上で、その前提のもとにデータから得られた分散比以上のデータが得られる確率を算出します。

F検定の結果、算出されたp値が基準よりも小さい値であれば、帰無仮説が棄却され、「グループの違いによって生み出された（成果指標の）分散は０でない」となります。この結果から「グループの違いによって、成果指標の得点の高低が説明される」と見なし、グループの違いが成果指標の得点に影響していたと判断されるのです。

例のデータでいえば、その中で算出された分散比6.64は、自由度（2, 15）のF分布に従うため、この分散比以上のデータが取得される確率をF検定で計算すると、p = .009となります。

このp値は、慣例的な基準である５％（p = .050）を下回っています。そのため、例のデータにおけるF検定では帰無仮説が棄却され、最終的に「研修参加の様相によって、コンプライアンス意識得点の高低が有意に説明されている」と判断されるわけです。

グループ間の違いを詳細に検証する　多重比較

ここまで説明をしてきたように、分散比を算出してF検定を実施することで、所属グループの違いによって成果指標の得点の程度に違いがあるか否かの判断ができました。

しかし、この分析で検証されたのは「所属グループが違うことによって、成果指標の得点の程度には違いがある」というおおまかなことだけです。言い換えれば、「具体的に、どこのグループ間で得点に違いがあるのか」は、まだ検証されていません。

分散分析において、この点を詳細に検証する分析を「多重比較」と呼びます。多重比較では、簡単に言えば「すべてのグループの組み合わせに対して、2グループの得点差を検証するｔ検定を行う」ことになります。

本コラムの最初に多重検定の問題を取り上げましたが、分散分析では、最初に分散比のF検定を行い「そもそも所属グループが違うことによって、得点に違いが生まれるといえるのか」を検証しておくことで、まずこの問題に対処しています。

分散分析の多重比較では、さらなる対処として「ｔ検定におけるｐ値を判断する際、その基準値を厳しくする」方法が用いられます。「下手な鉄砲も数打てば当たる」という例えに置き換えれば、試行回数を増やした分だけ、狙う的のサイズを小さくしていき、偶然にあたる可能性を小さくしていくイメージです。

多重比較における基準値を厳しく設定する補正計算法には、様々なものがあります。ここでは最もシンプルでわかりやすい補正法のひとつとして、Bonferroni法を紹介します[10]。Bonferroni法は、ｐ値の基準となる値に対して、検定を実施する回数を単純に割り算することで補正を行います。

例えば、Ａ研修・Ｂ研修・研修なしの３グループで得点を比較する場合、Ａ研修とＢ研修、Ａ研修と研修なし、Ｂ研修と研修なしで３回分のｔ検定が実施されることになります。

統計学的検定におけるｐ値の基準は慣習的に5%が用いられていますが、検定の回数は３回であるため、Bonferroni法による基準の補正を行うとｐ値の基準となる値は5%÷3≒1.67%に差し替えられます。

仮に、営業部・製造部・経理部・総務部・開発部といった５グループ間で何かの得点を多重比較しようとした場合、５グループすべてを比較する組み合わせのパターンは10通りあるため、ｔ検定も10回分実施されることになります。すると、Bonferroni法の補正によって、ｐ値の基準となる値は5%÷10＝0.5％に差し替えられます。

このように、帰無仮説の棄却判断において、下回らなければならないｐ値を補正計算によって厳しく設定することで、検定の試行回数増加に対処する手続きが取られるのです。

例のデータを用いて、Bonferroni法を用いた多重比較をやってみます。まず、A研修とB研修、A研修と研修なし、B研修と研修なしでそれぞれ、コンプライアンス意識の得点差からｔ値を算出し、ｔ検定を行います[11]。

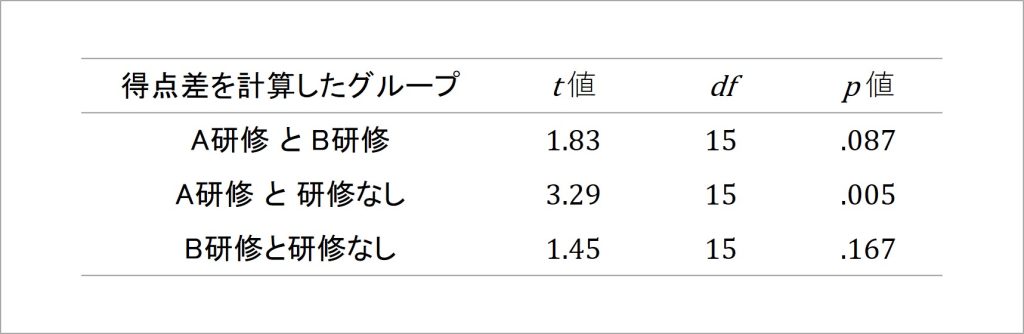
図１０　多重比較の結果

各グループ間にある得点差についてｔ検定を行うと、それぞれの得点差におけるｔ値が帰無仮説のもとで生じる可能性を表す、ｐ値が得られます。今回の多重比較では、ｔ検定を3回繰り返しているため、通常ならば5%を下回るか否かで有意な差か否か判断するところを、Bonferroniの補正で5÷3≒1.67％を基準に再設定し、判断するわけです。

すると、ｐ値が1.67%（p = .0167）を下回っているのは、A研修と研修なしの間にある得点差のみでした。この結果から、A研修のコンプライアンス意識の得点4.1点は、研修なしの得点3.3点より高く、統計学的に見てその差は０ではない、有意な得点差であると判断されます。

一方、B研修は、研修なしの得点3.3点に対して、3.8点と高得点でしたが、分散分析と多重比較の結果からこれらの得点差は０ではないと言い切れず、偶然生じたレベルの得点差だと解釈されるわけです。

図1再掲　研修参加によるコンプライアンス意識の高さの比較

ここで図１を再度見ると、得点だけ見ればA研修・B研修は研修なしよりもコンプライアンス意識が高くなっていました。そこから、「どちらの研修でも、参加すればコンプライアンス意識は高まりそうだ」と考えていました。

しかし、分散分析を行うことで、「研修なしと比較したB研修における得点の高さは偶然に生じた程度のものだが、研修なしと比較したA研修における得点の高さは有意な得点差」と判断できました。分散分析によって、研修の成果をより正確に判断できたわけです。

今回は、３つ以上のグループ間で得点差を比較する分散分析について解説しました[12]。グループ間の差異をより手広く正確に検証するための基本的な手法として、知っておくと便利な分析です。

 

参考文献

Hair, J. F., (2014). Multiple Regression Analysis. In J. F. Hair, C. B. William, J. B. Barry, & E. A. Rolph (Eds.), Multivariate Data Analysis (7^th edition), Englewood Cliffs, NJ: Prentice Hall.

森 敏昭・吉田 寿夫（編）（1990）. 心理学のためのデータ解析テクニカルブック　北大路書房

脚注

[1] 本コラムは、2021年1月20日の当社コラム「人事のためのデータ分析入門：「統計的に有意」とは何か（セミナーレポート）」（https://www.business-research-lab.com/210120-2/）に関連する内容となっています。合わせてご覧ください。

[2] 厳密には、「取得したデータで得られた結果”以上の大きな得点差となる”データは、帰無仮説を前提としたときにどのくらいの確率で生じると推定されるか」です。ここでは、専門家ではない初学者向けに理解を促す目的で、このように記述しています。

[3] 紹介する計算方法は分散を計算する基本的な考え方を直接取り上げたものであり、この方法以外に、偏差平方和や合計の二乗値を用いて一括計算する数式が存在します。本コラムでは、分散分析の考え方を初学者向けに紹介するものであり、一括計算の数式は初学者にはやや難解であることから、手間はかかるがより理解が容易な計算方法を扱いました。興味がある方は、参考文献の書籍（森・吉田, 1990）をご覧ください。

[4] イメージしやすくするため、各数値を小数点第２位で四捨五入して数字の見た目を簡単にした関係で、厳密な値とは異なっています。そのため、計算途中の数値にわずかなずれがあったり、また、例の元データで実際に分散分析をしても、後に提示するF値と同じ値にはならなかったりします。

[5]敢えて具体例を挙げるとすれば、各回答者の道徳意識や組織への愛着の程度、リーダーによる監督の厳しさなどが考えられます。いずれにせよ、「分析に含めていないあらゆる要因」によって生じる、研修参加で説明されないコンプライアンス意識の分散要素が、これに該当します。

[6] 厳密に記述すると、自由度は「観測値の総数から母集団を推定する母数の個数を引いた値」となります（Hair et al, 2014）。母集団を推定する際は、不偏推定量と呼ばれる統計量で必要な値（母数）を埋め合わせる計算が含まれます。それに対応する形で、各種統計量を計算する際に制約がかかり、それを自由度として扱います。そのため、分散分析に限らず、母集団について推測する各種分析では、自由度を計算に含めることで、制約が課された状態での推定計算を行うことになっています。

[7] 自由度の計算において、制約により引き算される数値は違ってきます。この違いを理解するための解説は難解であるため、別のコラムに譲ります。なお実践上は、データ解析ツール内で自動計算されるため、特に気にならない方はこの議論を深追いしなくても問題はありません。

[8] 本コラムでは等分散の検定を省略しています。そのため、自由度の計算では、厳密にはWelchの方法による補正計算も含める必要があります。

[9] この帰無仮説は、図８などで示した数式から「F値が０である」ことを指すように見えますが、分散分析における分散比の期待値の数式に則ると、帰無仮説は「F値が１である」になります。詳しくは、森・吉田（1990）を参照してください。

[10] Bonferroni法は、単純な補正方法であると同時に、非常に厳しい補正方法です。補正が厳しすぎることによる問題は、基準値を不要に厳しくしすぎることで、「あるグループの間には実質的な得点差が存在するのに、基準が厳しすぎるせいで”差がない”と判断される」ことです。このような問題に対応した補正方法として、Holm法やShaffer法もあります。

[11] ２つのグループ間の得点差比較（ｔ検定）に関する詳しい解説は、当社コラム「人事のためのデータ分析入門：『統計的に有意』とは何か（セミナーレポート）」をご覧ください。なお、多重比較で行うｔ検定では、通常のｔ検定と異なり、自由度は「グループの要因によって説明されない分散の自由度」を参照します。

[12] なお、本コラムで解説した分散分析はもっとも基本的なものであり（対応なしの一要因分散分析）、他にも様々なバリエーションがあります。

---

執筆者

能渡 真澄

信州大学人文学部卒業，信州大学大学院人文科学研究科修士課程修了。修士（文学）。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を，他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており，通常では捉えることが困難な，様々なデータの背後にある特徴や関係性を分析・可視化し，その実態を把握する支援を行っている。