2022年4月4日
多次元尺度法の基本的な考え方
自社が提供するサービスについて、顧客から様々な評価データを取得したとします。ここでは、自社サービスを利用している顧客に対して、以下の内容について評価を求めました。
- サービスの使いやすさ
- 問い合わせの気軽さ
- 契約料の安さ
- マニュアルの見やすさ
- サービス維持費の満足度
- 営業担当者の満足度
- 自社のイメージの良さ
- サービスの迅速性
- 費用対効果の良さ
上記の内容をそれぞれ10段階(0=評価は低い~10=評価は高い)で回答する構成で、複数の顧客にアンケート調査を実施しました。多くの場合、このようなデータでは、まず回答値を集計して評価が高いものを確認するでしょう。
その結果から、自社サービスにおいて顧客評価が最も高い内容がどれかを検証したり、逆に評価が低い自社サービスの弱点となる内容も見いだせたりするかもしれません。
あるいは、相関係数を算出して、ある内容に対する評価の高低は、他の内容の評価の高低とどの程度関連しているのか検証することもできます[i]。しかし、ただ相関係数を算出しても、すぐに想像できる結果が示されるのみに終わることも少なくありません。
例えば、「費用対効果の良さに対する評価が高いと、サービス維持費の満足度評価も高い」など、わざわざデータ分析しなくとも、「そうなるだろう」と直感的に想像できる結果しか示されないこともあります。
確かに、相関係数で示される指標間の対応関係の強さを把握することも重要です。しかし、すぐに思いつくような指標間の対応関係が示されても、分析としてはやや物足りなく感じるのではないでしょうか。
このような問題について、相関係数の情報をよりうまく扱うには、回帰分析や因子分析など、より高度な統計解析の手法を用いる必要があります。
本コラムでは、そのような応用的手法のひとつである「多次元尺度法」を紹介します。多次元尺度法は、相関係数を類似性の強さを表す指標と捉えて、複数の指標間の類似性を視覚化することに特化した分析です(Borg & Groenen, 2005)。
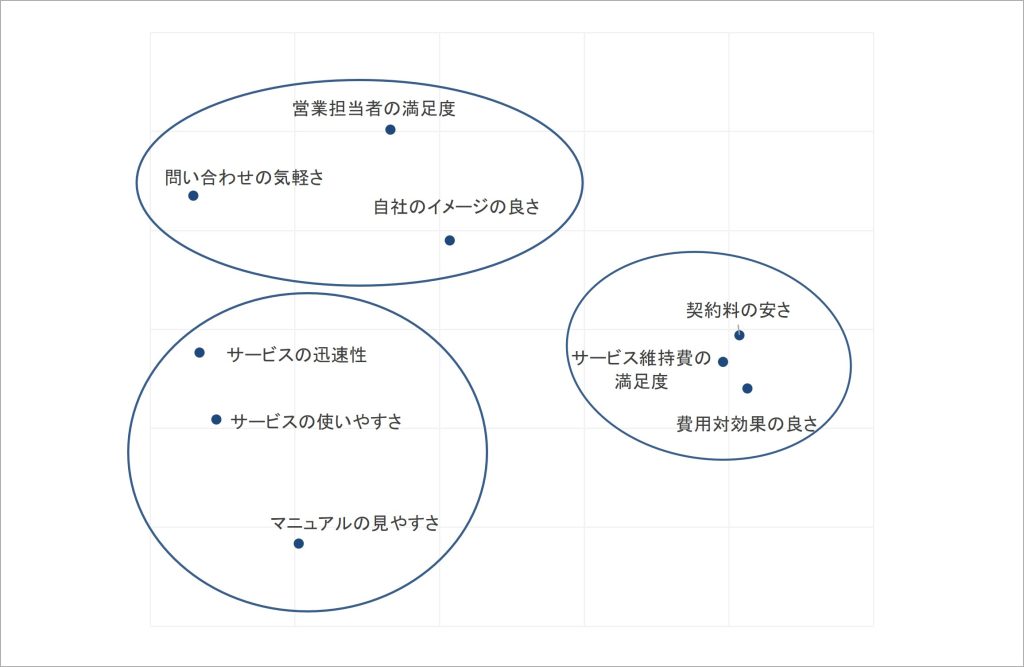
例えば、多次元尺度法を用いることで、以下の図のように指標間の対応関係を視覚化できます。
図1 多次元尺度法による分析結果の出力例
この図では、近い場所に位置する指標同士は類似性が高いことを表しており、遠い場所に位置する指標同士では類似性が低いことを表しています。相関係数の情報により、概念間の類似性の全体像が視覚的に把握できるようになるのです。
本コラムでは、相関係数で表された対応関係の情報を包括的に捉えて視覚化する、多次元尺度法について紹介します。
「距離」の情報を生かした相対的な位置関係の決定
最初に、多次元尺度法の根本にあるアイデアを追いつつ、相関係数がどのようにして集約されて上の図のような結果に至るのか、解説していきます。
ここで突然ですが、以下の問題を考えていただきたいと思います。問題への回答は、数学的に厳密な計算などを考えず、頭の中でパズルのように考えてください。
なお、作成した各図形の向きは問わず、全体の形状がおおよそ合っていれば正解とします。
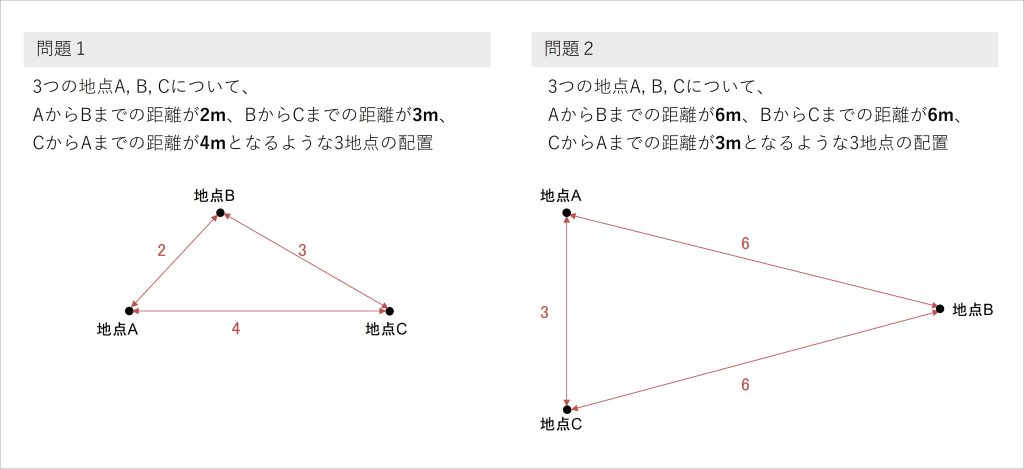
| 問題1:3つの地点A, B, Cについて、AからBまでの距離が2 m、BからCまでの距離が3 m、CからAまでの距離が4 mとなるような3地点の配置を平面上で示してください。
問題2:3つの地点A, B, Cについて、AからBまでの距離が6 m、BからCまでの距離が6 m、CからAまでの距離が3 mとなるような3地点の配置を平面上で示してください。 |
これらの問題の回答は、以下のようになります。皆さんは正解できたでしょうか。念のため、この問題に正解できないと、本コラムの内容を理解できないわけではありませんので、ご安心ください。
図2 問題1と問題2の答え
これらの問題について、各地点の配置を想像することができたでしょうか。この問題でお伝えしたかったポイントは、「各地点がそれぞれどのあたりにあるかという情報がない状態でも、各地点の相対的な位置関係は推測できる」ということです。
これらの問題で与えられた情報は、各地点の位置情報でなく、各地点間の距離情報でした。つまり、「各点の間の”距離”がわかれば、それぞれの点が互いにどのあたりに位置するか、相対的な位置関係を決めることができる」のです。
複数のものに対して、それらの間にある「距離」の情報がわかれば、それぞれの相対的な位置関係を決定することができます。このアイデアを踏まえると、「取得したデータから算出された相関係数から距離の情報が取り出せれば、各指標の相対的な位置関係が決定できる」とわかります。
より一般的な表現でいえば、「アンケート調査で取得したデータから、指標間の距離情報を取り出す」ことができれば、指標間の相対的な位置関係を把握できるわけです[ii]。
指標間の相関係数を距離情報と見なす手法
それでは、相関係数からどのようにして距離情報を取り出せばよいのでしょうか。実は、相関係数は値をわずかに加工することで、距離情報として扱える性質をもっているのです。
まず、あるデータを距離情報として扱うためには、以下の条件を満たす必要があります(Borg & Groenen, 2005)。
図3 あるデータを距離情報として扱うための条件(距離の公理)
これらの条件のうち、非負性は「任意の2点i, jについて、2点間の距離は必ず0以上の値をとる」ことを表します。これは、我々が普段の生活で、物の長さや移動距離などを表現する際に、必ずプラスの値で表現することからもわかるでしょう。
対称性は、「任意の2点i, jについて、2点間の距離はiからjへの値とjからiへの値が一致する」ことを表しています。これは、2つの地点A, B間の距離について、移動ルートが同じならばAからBへ向かう場合の距離とBからAへ向かう場合の距離は等しくなるということです。
三角不等式は「任意の異なる3点i, j, kについて、ある2点i, j間の距離は、必ず2点i, k間の距離と2点k, j間の距離の合計以下になる」ことを表しています。これは、3つの地点A, B, Cにおいて、地点Aから地点Cに直接向かう移動距離は、地点Aから地点Bを経由して地点Cに向かう移動距離よりも、必ず短くなるということです。
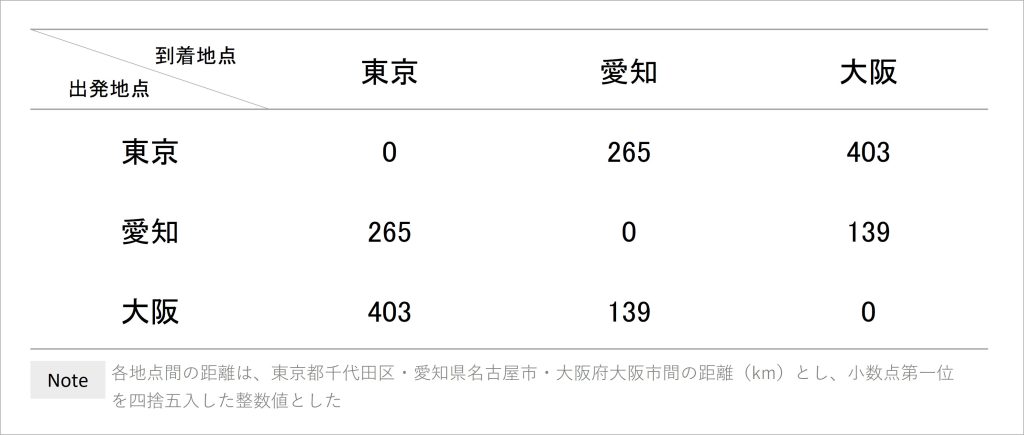
以上の条件を満たすデータは、距離情報として扱えると定められています。例えば、日本の三大都市とされる東名阪(東京・愛知・大阪)間の実際の距離(km)をまとめたものが以下の表です。
表1 三大都市間の距離をまとめた表(距離行列)
実際の距離を入力した表であるため、当然ながら、表内のデータは距離の条件を満たしています。まず、同じ地点を出発地点・到着地点とした場合の値は全て0となっており、異なる地点間で出発・到着した場合の値は全てプラスの値となっています。これが非負性です。
次に、例えば東京を出発して愛知に到着する場合の値と、愛知を出発して東京に到着する場合の値は等しくなっています。このような関係は、他の地域を出発・到着地点に選んでも常に成り立っています。これが対称性です。
さらに、東京を出発して大阪に到着する場合の値(403)は、東京を出発して愛知に到着し、愛知を出発して大阪に到着する場合の値の合計(265+139=404)よりも小さくなっています。このような関係は、地域をどのように選んでも成り立っています。これが三角不等式です。
このように、実際の距離データを整理してみても、距離の条件を満たしていることがわかります。距離情報として扱えるデータは、距離の条件を満たしているのです。表1のような状態で距離の条件を満たしているデータは、距離情報として扱えます。
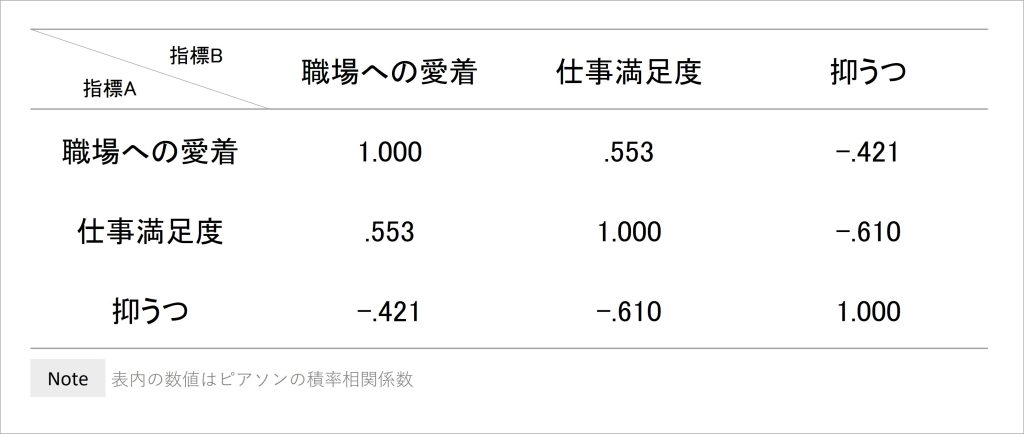
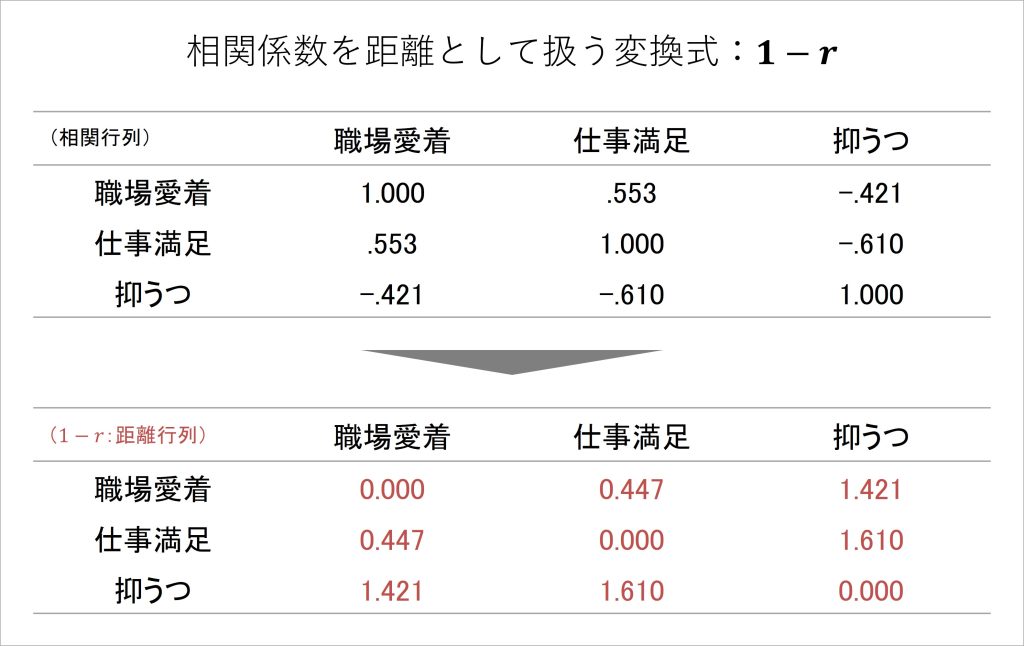
これに対して、相関係数の情報をまとめると以下の表のようになります。ここでは、別の架空データとして、職場への愛着、仕事満足度、抑うつのアンケート調査から算出された相関係数を表にまとめています。
表2 相関係数をまとめた表(相関行列)
表2のように、測定したデータ間で相関係数を算出し、表内に書き並べたものを相関行列と呼びます。相関係数は、2つの指標A,Bの共分散をそれぞれの標準偏差で割り算して求められますが、その計算において2指標A,Bのどちらを先に入れても、同じ相関係数が算出されます。
例えば、表2において、指標Aを「職場への愛着」、指標Bを「仕事満足度」とした場合の相関係数はr = .553です。また、指標Aを「仕事満足度」、指標Bを「職場への愛着」とした場合の相関係数もr = .553となっています。このことから、相関行列では対称性が成立しています。
しかし、相関行列を距離情報として扱おうとする際の問題として、指標A, Bに同じ指標を用いた場合の相関係数は、必ずr = 1.000となります。これにより、同一地点間の距離が0である必要がある中で、相関行列では同じ指標を取り上げた箇所では相関係数の値が0にならないため、非負性の条件を満たしません。
また、相関係数はr = -1.000~+1.000の値をとる、つまり負の値にもなる特徴があります。表2でも、例えば職場への愛着と抑うつの相関係数はr = -.421であり、負の値が現れています。これも、非負性の条件を満たさない性質です。加えて、いくつか計算してみると、三角不等式も成立していないことがわかります。
このように相関行列は、対称性は満たしつつも非負性や三角不等式を満たさないため、そのままでは距離情報として扱うことができません。
そこで、この問題に対応して、相関行列を距離情報として扱えるようにする「1から相関係数を引き算した値を用いる」手法が提案されています(cf., Cox & Cox, 2008)[iii]。
図4 相関係数を距離情報に変換する手続き
具体的な方法としては、図4のように、相関行列におけるすべての相関係数について、1からその値を引き算する計算を行うだけです。
この手続きによって、まず、表内の値が取りうる値の範囲は、-1.000~+1.000から、0.000~2.000になります。取りうるすべての値が0以上の値となるため、非負性を満たすことになるわけです。
また、図4の数値を見ると、1 – rをした後の表では、すべての値で三角不等式が成り立っているおり、対称性も保たれていることがわかります。これによって、距離として扱うための全条件を満たせたため、1 – rをした後のデータは距離情報として扱えるようになります。
このように、相関係数をまとめた相関行列に対して簡単な計算処理を施すだけで、距離を表すデータとして活用することができます。それにより、先に示したアイデアを活用し、概念間の位置関係が視覚化できるようになるのです。
相関係数から得られた距離データの意味
上記の手続きにより、相関係数が距離情報として扱えるようになりました。しかし、相関係数そのものは距離を表すものではなく、指標間の対応関係を表すものです。
相関係数を距離情報と見なせるようになったとしても、その数値が何を意味しているかわからなければ、視覚化できてもその解釈ができません。相関係数を1 – rと変換させた数値は、どういった意味を持つのでしょうか。
相関係数は、2指標の得点の対応関係を表すものですが、その解釈のひとつとして、2指標の類似性の高さを表すものとしても扱われています(Borg & Groenen, 2005)。
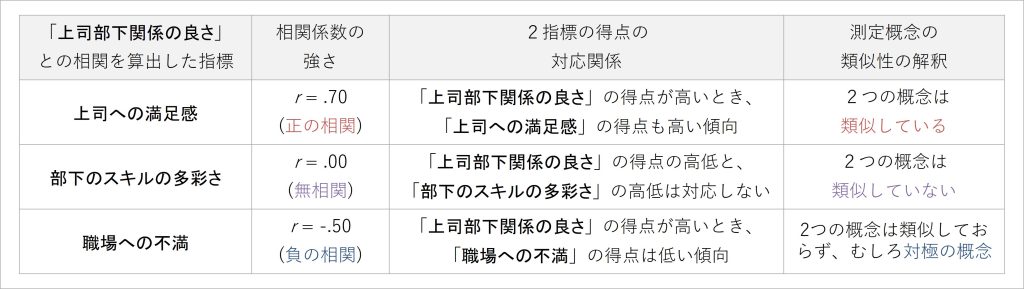
例として、上司部下関係の良さと様々な相関を取る各指標について、得られた相関係数と類似性の解釈の関係性を下の表にまとめました。例のデータは、部下に「上司部下関係の良さ」「上司への満足感」「部下のスキルの多彩さ」「職場への不満」を評価させ、それらの指標間で相関係数を算出したイメージのものです。
表3 相関係数の強さに応じた測定概念の類似性の解釈
表3を見ると、部下が評価した上司部下関係の良さと上司への満足感は、強い正の相関があります。それが統計学的に意味することは、上司部下関係の良さの得点が高いとき、上司への満足感の得点も高い傾向があるということです。
これらの得点間の関連から、2つの概念には互いに似通った部分があると捉えて、「2つの概念は類似している」、すなわち類似性が高いと解釈されます。
上司部下関係の良さと部下自身のスキルの多彩さは、無相関です。それが統計学的に意味することは、上司部下関係の良さの得点の高低と部下のスキルの多彩さの得点の高低は、特に対応していない無関連なものであるということです。
これらの得点間の関連から、2つの概念は互いに似通った部分がないと捉えて、「2つの概念は類似していない」、すなわち類似性が低いと解釈できます。
そして、上司部下関係の良さと職場への不満は、中程度の負の相関があります。それが統計学的に意味することは、上司部下関係の良さの得点が高いとき、職場への不満の得点は低い傾向があるということです。
これらの得点間の関連から、2つの概念には何らかの真逆な特徴があると捉えて、「2つの概念は類似していない、むしろ対極に存在する概念である」、つまり類似性が低いどころか真逆の特徴を持っていると解釈できます。
このように、相関係数の正負やその値の強さに応じて、取り上げた2指標間の類似性を評価することができるのです。そして、これらの解釈を1 – rの値と対応させると、以下の表のように整理できます。
表4 2指標の対応関係と類似性および1 – rの値
1 – rの値は、相関係数がr = 1.000のときに0になります。1 – rを距離の情報として捉えると、その値が0であることは距離が0であることと同義です。2指標が測定した概念が非常に類似しているとき、距離の情報は0になるということです。
また、1 – rの値は相関係数がr = .000のとき1になります。相関係数がr = .000と無相関なとき、2指標が測定した概念が類似していないことを踏まえると、1 – rという距離のデータが0から1へと大きくなると、2つの概念の類似性が低くなっていると解釈できます。
そして、1 – rの値はr = -1.000のときに2になります。相関係数がr = -1.000と負の相関があるときは、2つの概念が類似していないことを超えて、対極に存在するものであると解釈されます。要するに、距離を表す1 – rの値が1から2へと大きくなると、概念間の類似性はさらになくなり、対極に位置する概念だと解釈されるようになるのです。
以上を踏まえると、相関係数を距離に変換した1 – rの情報について、2指標間の距離が0に近いほどそれらの類似性は高く、そこから距離が大きくなるほど類似性が低くなっていくと解釈できます[iv]。
これにより、相関係数を多次元尺度法によって視覚化した図において、指標間の距離の大きさは、そのまま「それぞれの指標がどの程度類似しているか」を表していると見なせます。したがって、多次元尺度法で視覚化された各指標の位置づけにおいて、位置が近い概念同士は類似したものであると解釈できるわけです。
相対的な位置関係の視覚化とその解釈
上記の手続きによって、相関係数が距離情報として扱えるようになり、多次元尺度法が活用できるようになりました。
ここからは、相関係数を距離の情報に変換した後で、具体的に多次元尺度法を用いて分析を進めると、どのようなプロセスを経て最終的な出力に至るか解説していきます。
なお、多次元尺度法の内部で行われる具体的な計算プロセスは、行列の計算を含む非常に複雑なものであり、初学者でなくとも非常に難しい内容になるため、本コラムでは解説を割愛します。詳細な計算内容に興味がある方は、非計量多次元尺度法(nonmetric multidimensional scaling)にて検索することをお勧めします。
それでは、最初に示した架空例のデータを用いて、実際に多次元尺度法の分析を行っていきます。
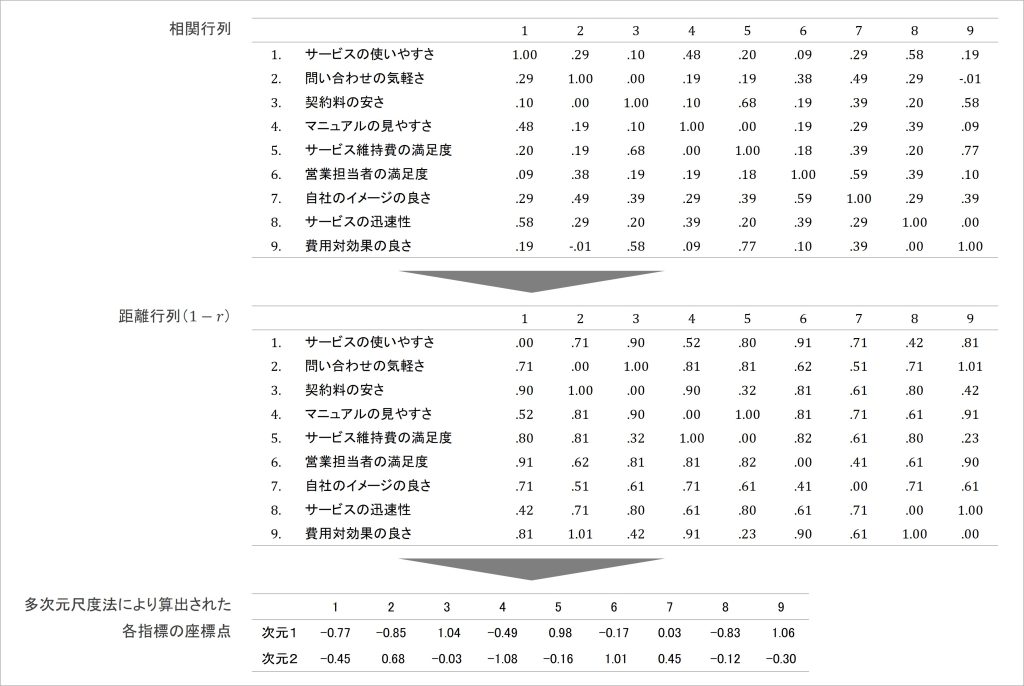
まず、例のデータにおいて相関係数を並べた相関行列を作成し、その後1 – rの計算を施した距離行列に変換します。そして、作成した距離行列に対して多次元尺度法による解析をかけると、縦横に伸びる2軸を想定した2次元上に対する、各指標の位置情報(座標点)が算出されます[v]。
図5 相関行列が2次元上の座標点に変換される展開
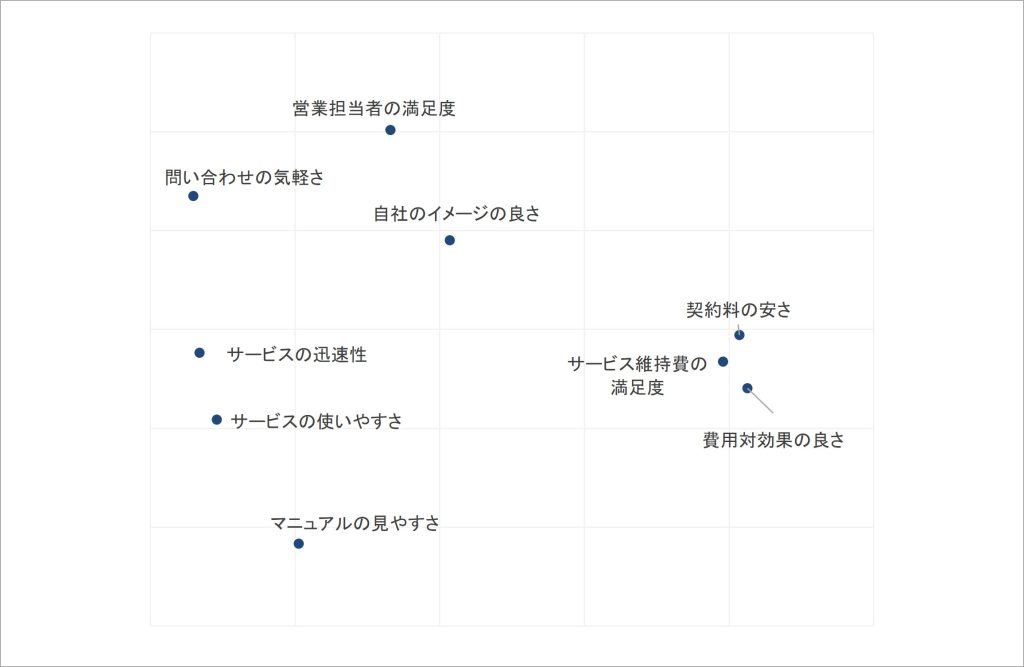
ここで、最終的に算出された座標点が、最初に示していた図における、各指標がプロットされる点になります。したがって、これらの点をプロットした図を作成すると以下のようになります。
図6 座標点をプロットした図
このようにして、多次元尺度法の分析を用いることで、相関係数の情報から各概念の位置関係が視覚化することができます。
ところで、最初の図では、この出力結果に円を描き、どのようなまとまりがあるかさらに明確化していました。それは、各点の距離が近い順にまとまりを形成していき、最終的にどのようなまとまりが構成されるかを検証する、「クラスタ分析」と呼ばれる分析の産物です。
クラスタ分析も距離行列を用いた手法になり、多次元尺度法と親和性の高い分析法です。この分析は、また別の機会に紹介していきますが、多次元尺度法と併用することで、データドリブンに各点のまとまりを表現できるようになります。
図1再掲 多次元尺度法とクラスタ分析を組み合わせた指標間の類似関係の視覚化
多次元尺度法の結果として示された、この図では、近い位置にあり、まとまりを形成する指標は類似性が高いと見なすことができます。それにより、複数の指標から見いだされる特徴を大まかに解釈することができるようになります。
例えば、図1左上のまとまりは、その内容から「サービスの対応窓口の従業員への好評」、右のまとまりは「費用面での好評」、左下のまとまりは「サービスのユーザビリティの好評」と解釈できます[vi]。複数の指標で測定された顧客による評価情報は、上記の意味合いを持って評価の程度が共起していると理解できるわけです。
多次元尺度法の注意点
多次元尺度法の活用において注意すべき点は、相関係数の推定精度により視覚化された結果の精度も変わることです。
本コラムで紹介した多次元尺度法は、調査で得られた相関係数をもとに距離のデータを作成し、2次元上の座標点を算出する手続きを取っていました。仮に、調査人数が少ないなど問題があれば、最初に算出された相関係数の値は、その後の調査で大きく違った値をとる可能性が高くなります。
距離情報の計算のもとになる相関係数の値が変われば、当然、最終的に出力される図も違ってきます。組織サーベイなどで数百名を超えるデータを収集することが困難な場合も多いため、サンプルサイズが小さいデータにおいて分析する際は、現時点での暫定的な結果と解釈するのが安全でしょう。
ただ算出するだけで終わっていた相関係数の情報も、多次元尺度法を用いることで、違った見せ方で表現することができます。データの視覚化テクニックとして、ぜひ知っておきたい技術といえるでしょう。
脚注
[i] 相関係数については、当社コラム「人事のためのデータ分析入門:「相関」とは何か(セミナーレポート)」にて解説しています。ご参照ください。
[ii] この一般化した言い換えは、「相関係数でなくても、距離情報と見なせる調査データならば、多次元尺度法による対応関係の視覚化は可能である」ことを表すものです。例えば、様々な清涼飲料水が互いにどの程度似たものかの類似度評価などが該当します。
[iii] ほかに、各指標の得点を標準化したり、すべての相関係数が正の値になるよう各指標の得点を適宜逆転してから、1 – rを計算する手法もあります(Wilkinson, 2002)。なお、すべての相関係数が正の値になるよう変換する手法を用いた場合、単純な相関係数の大きさが強い概念同士が近い場所に位置づけられる図が出来上がります。その手法を用いるか否かは、データ分析の目的によります。
[iv] このような特徴から、相関係数を1 – rで変換した後の行列は非類似度行列と呼ぶ方が適切です。本コラムでは、最初に説明した距離による位置関係の把握のアイデアとの接続性を高めるために、「距離」を前面に出した表現を一貫して使用しています。
[v] 厳密には、「相関係数に基づく複数の距離情報を、いくつの次元で集約するのが良いか」の判断を、ストレス値に基づいて行い、その評価をするフェーズが必要です。
[vi] このような、「データの背後に存在する何らかの傾向や特徴を検証したい」という分析目的をそもそも持っていたならば、それに特化した「因子分析」と呼ばれる分析法を用いた方が適切かもしれません。
引用文献
Borg, I. & Groenen, P. (2005). Modern Multidimensional Scaling: Theory and Applications (2nd ed.). New York: SpringerVerlag.
Cox, M. A., & Cox, T. F. (2008). Multidimensional scaling. In C. Chen, W. Härdle, & A. Unwin (Eds.), Handbook of data visualization (pp. 315-347). Springer, Berlin, Heidelberg.
Wilkinson, L. (2002). Multidimensional scaling. Systat, 10(2), 119-145.
執筆者
信州大学人文学部卒業,信州大学大学院人文科学研究科修士課程修了。修士(文学)。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を,他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており,通常では捉えることが困難な,様々なデータの背後にある特徴や関係性を分析・可視化し,その実態を把握する支援を行っている。