このコラムは、同じ対象者から同じ指標を複数回取得した際に使うことができる、「潜在差得点モデル」（McArdle & Hamaguchi, 2001; McArdle, 2009）について紹介していきます （※1）。この分析手法では、複数回取得した各種指標のデータを用いて、その得点の変化同士の関連を検証していきます。研修実施や半期ごとの従業員の変化について、より詳細にアプローチできる枠組みです。潜在差得点モデルを用いれば、「従業員への施策が個々の従業員に何らかの変化を生み出しているのか」や、「従業員の中で生じた変化が、どういった物事と関連を示しているのか」が検証でき、意思決定の助けになります。

まずは具体例から見ていきましょう。

複数回取得した指標の変化に着目する

ある会社（ここでは「A社」と呼びます）が、「従業員のモチベーションや幸福感を向上させることを目指して、協調的な組織風土を社内に浸透させよう」と計画しました。この考えは、より具体的には「協調的な組織風土が社内に浸透すれば、従業員の協調性や会社への愛着が高まり、それによって仕事へのモチベーションが高まり、良い環境で働けることで幸福感の向上も果たせる」という仮説に基づいていました。これらのプロセスをモデル化したものが、以下の図です。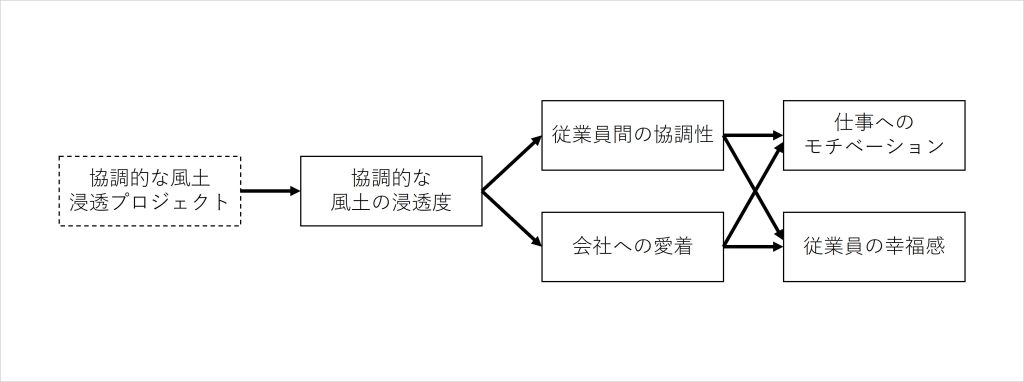

図１　風土浸透プロジェクトの効果に関する仮説モデル（架空の事例）

図1のモデルを想定して、A社は従業員から参加者を募って組織風土の浸透プロジェクトを実施し、プロジェクトの有効性を評価しようと考えました。そのために、まずは仮説で取り上げた５つの指標についてプロジェクト実施前にアンケート調査を行い、その後しばらくしてからプロジェクトを実施して、プロジェクトに参加した従業員と不参加の従業員それぞれに、同様のアンケート調査を行いました。

各指標を２回ずつ測定した調査データから、「プロジェクトの参加前後で、各指標の得点は上昇したか」や「プロジェクト参加者と不参加者で、各指標の得点に顕著な違いは見られたのか」を検討するのが狙いです。

以上の手続きを経て、A社では、５指標に関して以下のようなデータが得られたとします。なお、５指標は全て１～５点の間で得点化されており、得点が高いほど、その指標が捉える特徴がより良い状態であることを表しています。

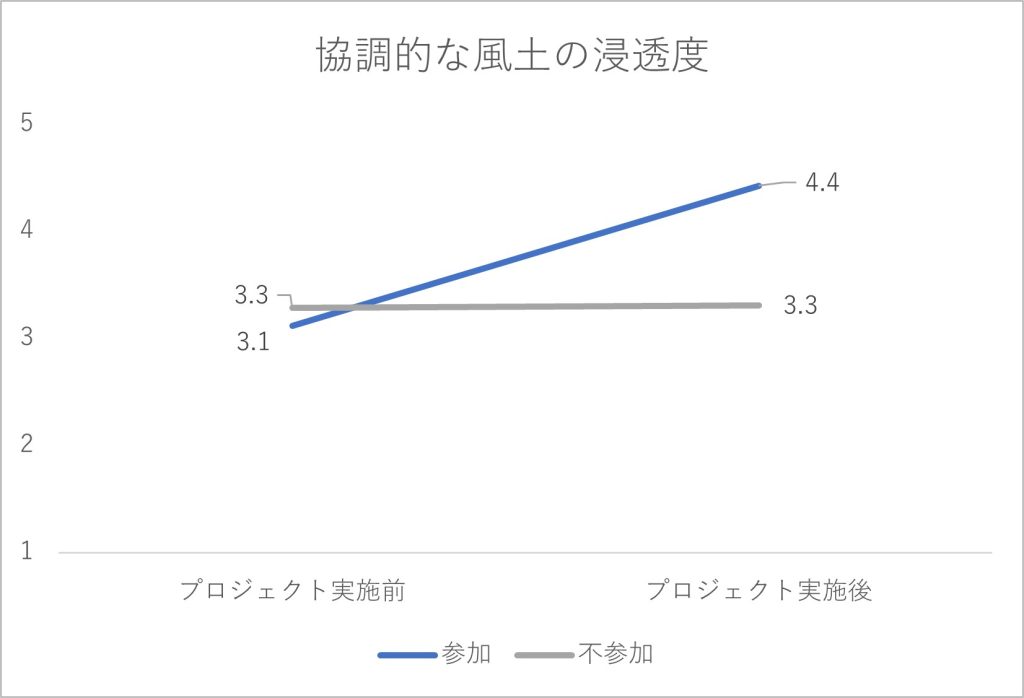
図2－1　協調的な風土の浸透度に関する集計結果

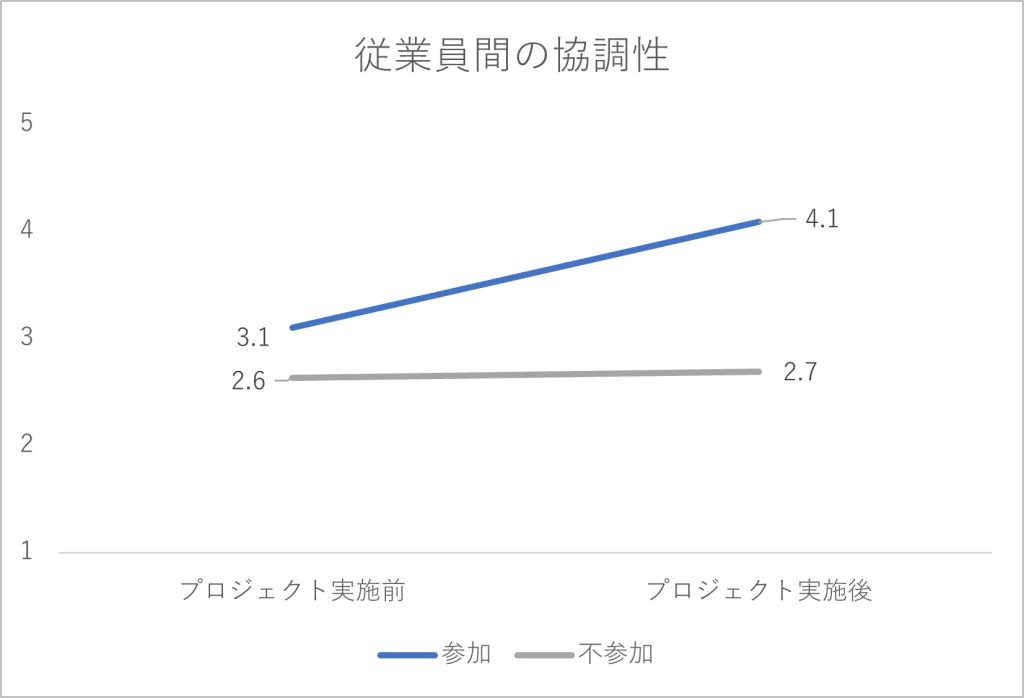
図2－2　従業員間の協調性に関する集計結果

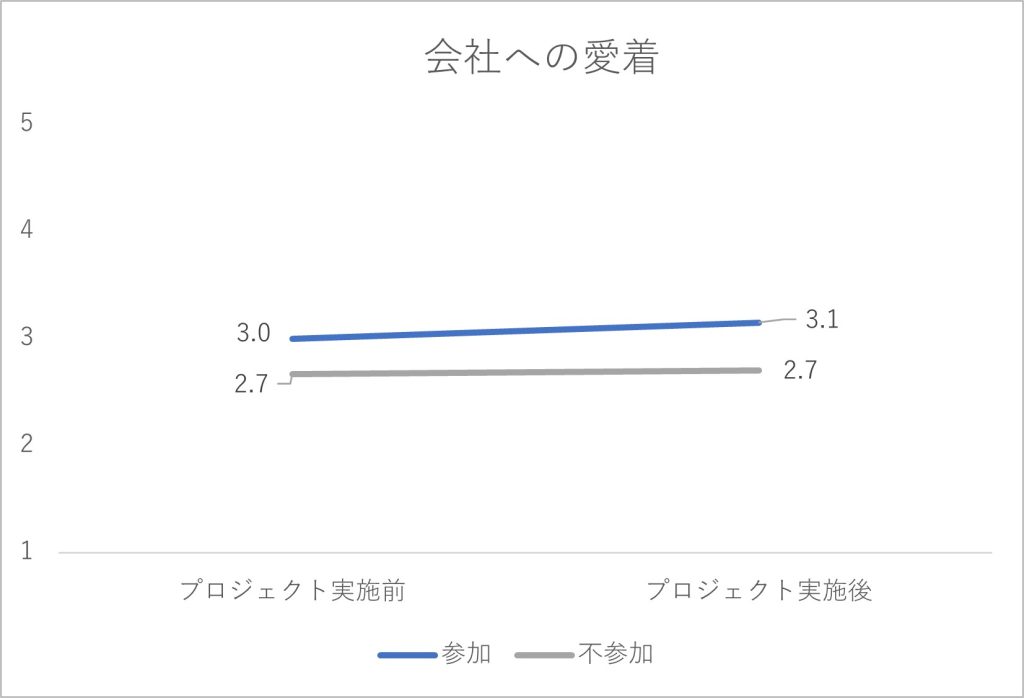
図2－3　会社への愛着に関する集計結果

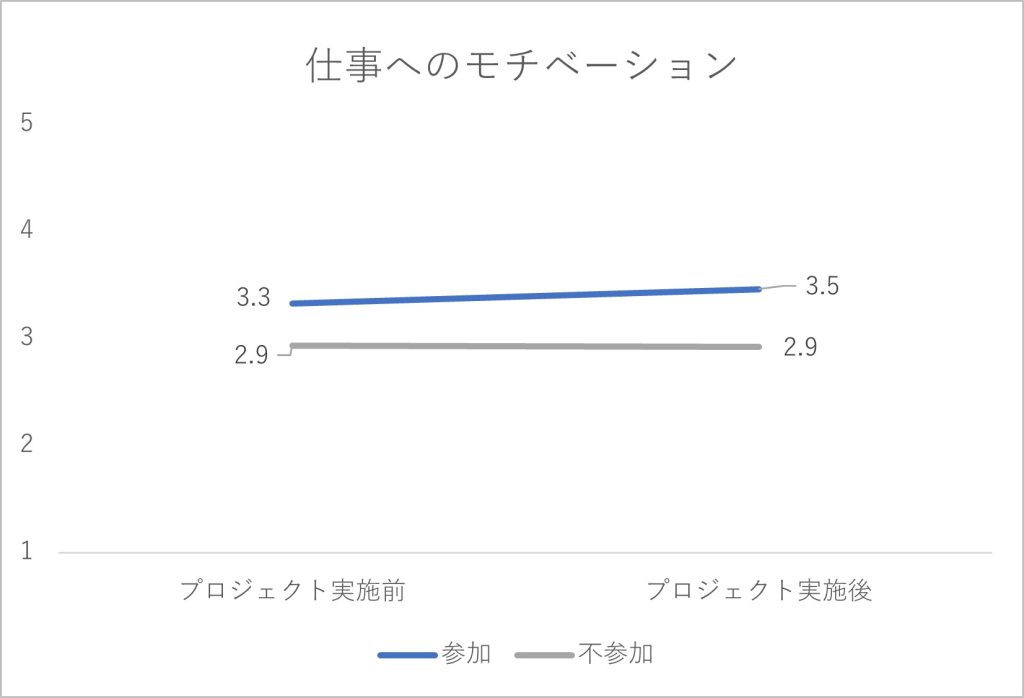
図2－4　仕事へのモチベーションに関する集計結果

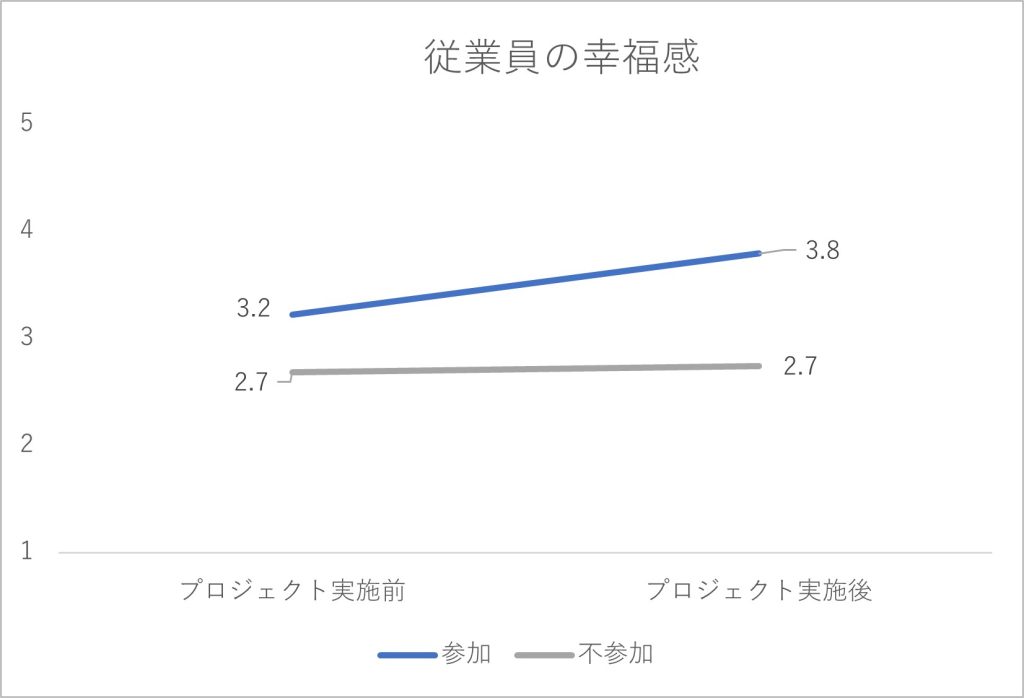
図2－5　従業員の幸福に関する集計結果

プロジェクト実施の結果として、プロジェクトに参加していない従業員では５指標の得点がほぼ横ばいで変化していません。他方、プロジェクトに参加した従業員では、特に「協調的な風土の浸透度」「従業員間の協調性」「従業員の幸福感」の指標で得点が右肩上がりの傾向を見せており、「プロジェクト実施に効果はあっただろう」と判断されるかもしれません。

仮に、参加者・不参加者それぞれにおいて、全体で生じたこれらの変化が存在したことを検証するならば、例えば、分散分析を用いて得点差が有意に０でないか確認した上で、その差がどの程度のものかを判断するのが良いでしょう。

しかしながら、実はこれらの検証で得点差を確認・検討しても、まだ検証ができていないところが存在します。それは、「各指標において個々の従業員に生じた変化が具体的にどの程度なのか」や、「従業員の中で生じた組織風土の浸透度上昇が、以降に続く各種指標の上昇と結びついているのか」といった、変化そのものに関する詳細な検証です。

各指標の得点変化に焦点を当てた方が良い理由は、最初に述べた通り、それがより正確な意思決定の助けになるからです。例えば、モチベーションや会社満足感など、着目したいアウトカム指標に関して、「アウトカム指標が高い従業員の特徴」を検証することと、「従業員それぞれが持つアウトカム指標をプラスに変化させる特徴」を検証することは、似て非なるものです。

「仕事パフォーマンスが高い従業員は、毎日早朝ランニングを繰り返していた」からと言って、早朝ランニングをしていない従業員たちにそれを実施させたとしても、仕事パフォーマンスが高まるとは限りません。あるアウトカム指標が高い人の特徴と、そのアウトカム指標をプラスに変化させる特徴は、異なることも多いのです。

この問題は「相関関係」と「共変関係」の違いとして説明されています（南風原, 2002; 村山, 2012）。「早朝ランニングしている人は、仕事パフォーマンスが高い」など、ある特徴に関する個人間差、ひいては、その特徴の有無で分かれる集団間の差異で捉えた関連性を相関関係と呼びます。他方で、「ある個人が早朝ランニングを習慣づけると、その人の仕事パフォーマンスも増加する」など、ある特徴に関する個人内の変化と、他の特徴の個人内変化における関連を共変関係と呼びます。

先ほど示したような平均値を比較する検証方法は集団間の得点差を検証するものであり、個々の従業員の中で生じた得点の変化を捉えていません。そのため、「プロジェクトの参加によって各従業員にどの程度の得点上昇が生じたのか」や、「各指標における得点の変化は、どのように関連しているのか」については、ここまでの分析結果で把握することはできません。

得点の変化同士の関連を把握することで、例えば「仕事のモチベ―ションの向上には、従業員間の協調性の向上が関連していた」ことがわかれば、「協調的風土の浸透プロジェクトでは、風土浸透と同時に協調性を発揮しやすい取り組みも増やした方が良い」など、従業員に変化を生み出す戦略を、より適切に立案する助けになります。このように、個々の従業員に生じた様々な変化の間にある関連、すなわち共変関係に焦点を当てたアプローチは、より効果のある戦略を考案していく上で有効です。

潜在差得点モデルの分析は、共変関係と相関関係を同時に扱い（Könen & Karbach, 2021）、概念間の関連をより精緻に検証できる枠組みを提供します。この分析はやや高度な手法であるため、すぐに現場に導入することは難しいかもしれませんが、まずはこの分析の魅力に触れていただければと思います。

潜在差得点モデルとは （※2）

潜在差得点モデル（Latent difference score model: McArdle & Hamaguchi, 2001; McArdle, 2009）とは、構造方程式モデルと呼ばれる分析枠組みを生かした応用的な手法の一つです。

構造方程式モデルとは、分析者が構成した分析モデルにおいて、モデルで取り上げた複数の指標の間にある関連性を一挙に分析する手法になります。この分析では、構成した分析モデルに対する取得したデータのあてはまりの良さや、種々の指標間の関連の強さが推定され、分析モデルの適切性や取り上げた指標間の関連を全体的に把握することが可能です （※3）。

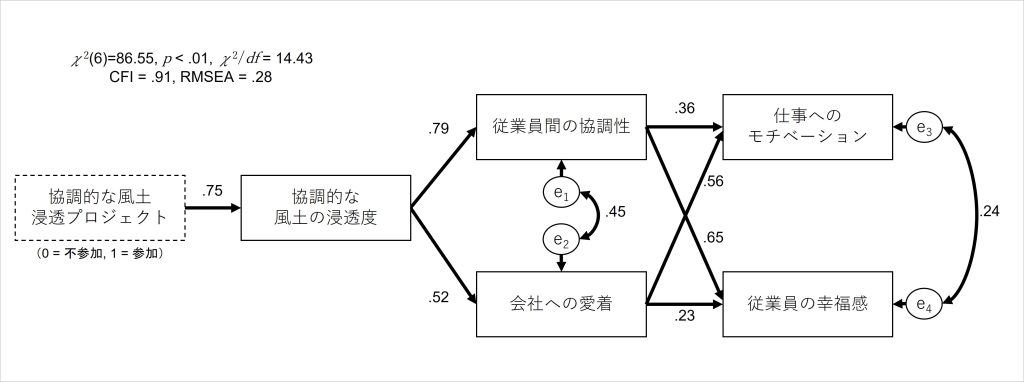
構造方程式モデリングの分析は、例えば図１を構成した分析モデルを設定し、取得したデータをこのモデルに当てはめることで、図３のような分析結果が出力されます。

図３　構造方程式モデリングの分析例

片矢印（パス）は、矢印のスタートに位置する指標が影響指標（独立変数）、矢印が刺さっている指標が成果指標（従属変数）として関連の強さを推定した結果の数値になっており、パス係数と呼ばれています。

この数値は、重回帰分析における標準化偏回帰係数と同じものです。つまり、パス係数は-1.00～+1.00をとり、数値の絶対値が大きいほど２つの指標間の関連性が強く、正の値であれば「影響指標の値が大きいほど、結果指標の値も大きくなる」、負の値であれば「影響指標の値が大きいほど、結果指標の値は小さくなる」ことを表します。

また、円の中にeと書かれたものは「影響指標によって説明されない、成果指標が持つ独自の要素」を表す残差であり、両矢印は２つの成果指標が持つ残差間の相関係数を表しています（※4）。

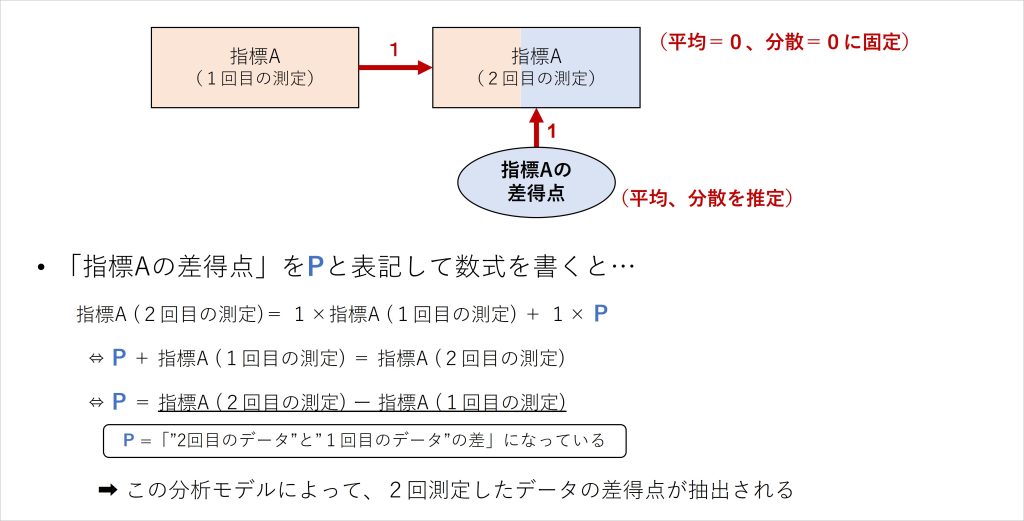
構造方程式モデリングの応用にあたる潜在差得点モデルでは、ある指標を複数回測定したデータについて、最初に測定されたデータの得点と二度目に測定されたデータの得点の差を分析モデル上に抽出して扱います。具体的には、図４のようにして２回測定されたデータの差（差得点）を抽出します。

図４　潜在差得点モデルによる差得点の抽出

モデル構築やその背後にある平均や分散に関する設定は専門的な議論を含むため割愛しますが、ここで把握しておきたいのは、このモデル構築で行っていることが「２回測定された指標Aのデータを用いて、１回目と２回目に測定したデータの差得点を抽出している」ことです。

ここで取り上げられた差得点が、各回答者における指標Aの変化の程度を表すものになります。この差得点を複数の指標を用いて抽出していくことにより、種々の指標における個人内の得点変化同士の関連、すなわち共変関係を検証していくのが、潜在差得点モデルの狙いです。

さらに、潜在差得点モデルでは、最初に測定したデータを「その指標において、回答者が元々その特徴を持っている程度」として扱うこともできます（Könen & Karbach, 2021）。つまり、最初に測定したデータがその指標が捉える特徴がもともと高い人や低い人といった個人差、すなわち相関関係を扱えるものになります （※5）。

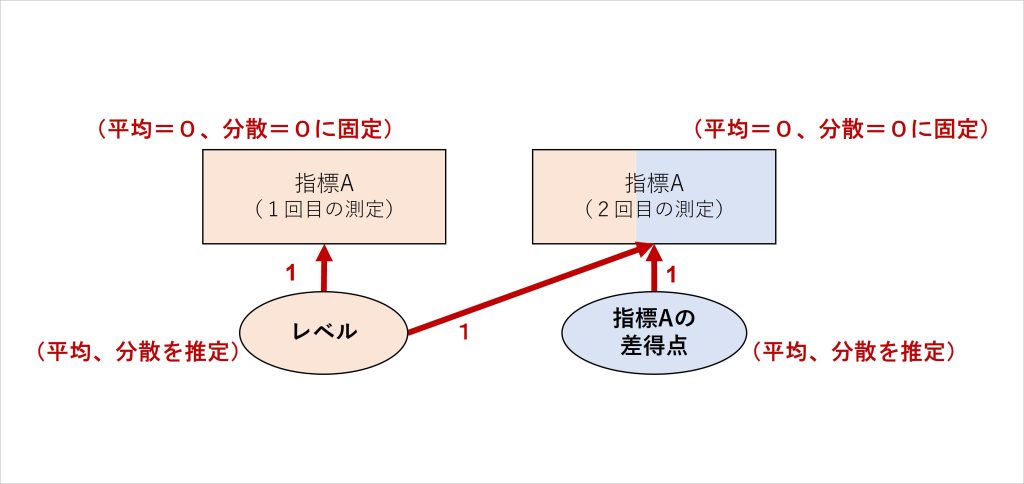
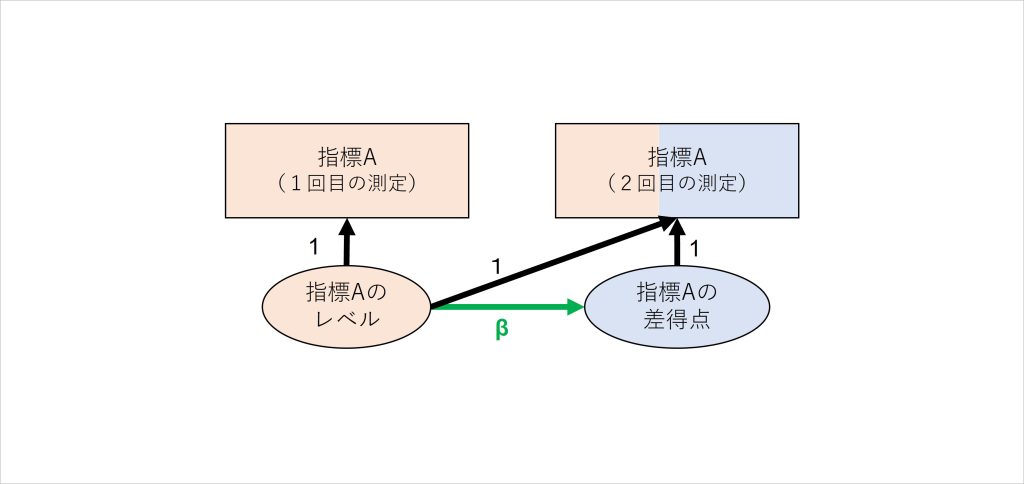
この点を明確化するために、最初に測定したデータに対して図５のようにモデルを再構成し、「レベル」として抽出・表現する方法もあります（Hertzog & Nesselroade, 2003）。

図５　最初に測定した指標からも、得点要素を抽出する分析モデル

モデルの見た目が変わり、新たに抽出されたレベルという指標が生まれていますが、内容は図４と同じであり、相関関係と共変関係を明確にモデル化しただけのものです。

このようにして、潜在差得点モデルでは、分析において相関関係と共変関係を扱える２つの指標をモデル上に抽出し、それぞれ検証を行っていきます。

潜在差得点モデルの特長：得点の変化を詳細に検証できる

潜在差得点モデルが持つ特徴の一つに、「各指標で生じた得点の変化を詳細に評価できる」ことが挙げられます。潜在差得点モデルでは、２回測定した指標からレベルと差得点を抽出しますが、この差得点について、その平均値と分散の大きさが最初に推定されるのです （※6）。

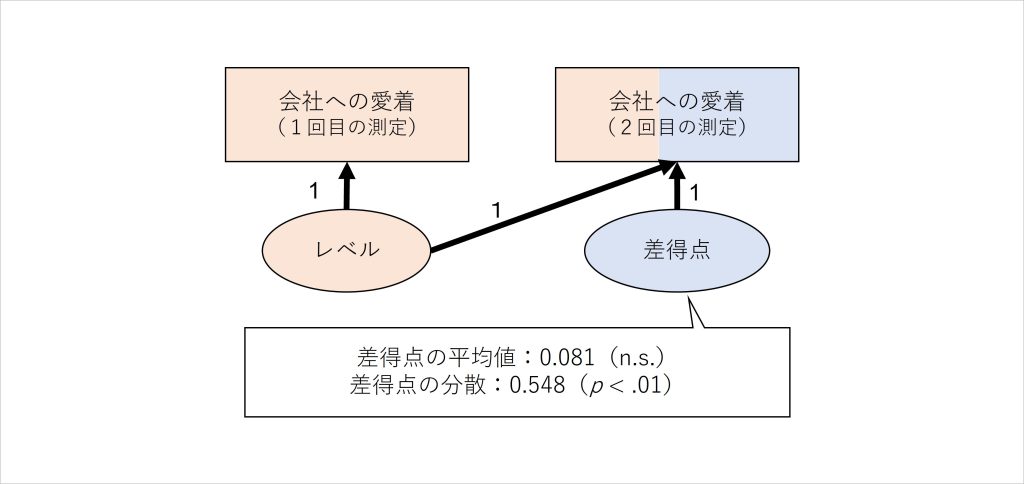
図６　差得点において推定された平均値と分散の例

例えば図６のように、潜在差得点モデルによって会社への愛着のレベルと差得点を抽出したとします。その際、差得点について平均と分散が推定され、それらの値に対して「統計学的に、０よりも大きい/小さいといえるか」に関する統計学的検定結果も付記されます （※7）。

ここで推定された差得点の平均値は、「各回答者において、２回の測定の間に、その指標の得点が平均してどの程度変化したのか」を表すものです。つまり、図６で推定された差得点の平均値は「各回答者において、２回の測定の間に、会社への愛着の得点が平均してどの程度変化したのか」を表しています。

図６のモデルでは浸透プロジェクトへの参加・不参加を含んでいないため、その区分けを無視した全回答者の推定値が算出されていますが、差得点の平均値は0.081でn.s.となっています。平均値0.081は「全回答者において、平均して会社への愛着が、２回の測定の間に0.081点増加している」ことを表しています。

そして、ここで示されたn.s.はnon significance(有意でない)、つまり「この推定値は、統計学的に見て有意に0より大きい・小さいといえない」ことを意味しています （※8）。これらを総合すると、「会社への愛着は、２回の測定の間で平均して0.081点増加していたけど、この得点増加は0より有意に大きいとは言えない」という結果です。

また、ここで推定された差得点の分散は、「２回の測定の間で生じたその指標の得点差は、回答者ごとにどの程度ばらついているのか」を表すものです。分散の値そのものは直感的な理解に使いにくい指標ですが、ポイントはそれが有意か否かです。

図６では、分散の値はp < .01で有意な値であると判断されています。これは、「２回の測定の間で生じたその指標の得点差のばらつきは、統計学的に見て有意に0ではないといえる」ことを表し、それはつまり「会社への愛着の得点差、つまり得点の変化には回答者ごとに違いが存在する」ことを意味しています。平均が0.081なので、人によっては、会社への愛着がプラスに増加したり、逆にマイナスに減った人もいるということになるわけです。

差得点に有意な分散が存在するということは、その指標において得点の変化の程度が多様であることを表すため、「得点の変化の違いを説明する、何らかの要因がある」と判断して、この差得点に対する影響指標を探る出発点となります。図６に合わせて言えば「会社への愛着の増加や減少を説明する要因が存在する」ということです。

このように、潜在差得点モデルで差得点を推定することにより、各指標の得点に平均してどの程度の変化が生じたのか、また、その変化は回答者によって違っているといえるのかが判断でき、その後の分析の足掛かりとなるのです。

潜在差得点モデルの特長２：相関関係と共変関係を同時に扱った分析ができる

また、潜在差得点モデルが持つ特長は「個人差・集団差に関する相関関係の検証と、個人内変化に関する共変関係の検証を、一つの分析モデル内で同時に行える」ことです（Könen & Karbach, 2021）。これを生かすことで、２回測定したデータが持つ様々な特徴を検証することができます。

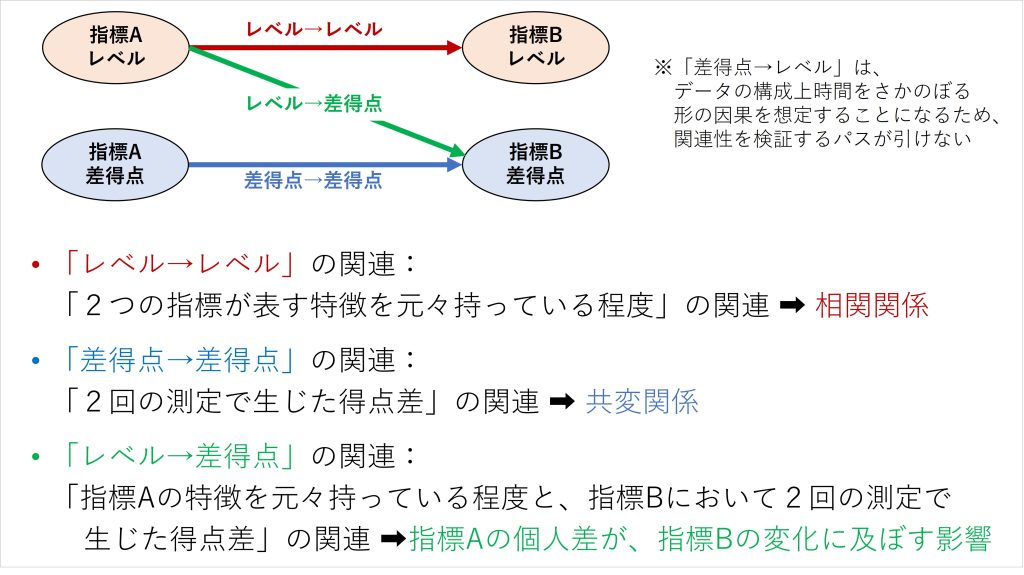
図７　レベル・差得点の関連が意味すること

２つの指標のレベル同士の関連を表すパスは、「指標Aの程度が高い人では、指標Bの程度がどの程度の高さになるか」を意味しており、これは個人差・集団差に関する相関関係を検証するものになります。

また、２つの指標の差得点同士の関連を表すパスは、「２回の測定の間で、指標Aの程度が回答者の中で大きくなったら、それに対応して指標Bの程度はどの程度大きくなるのか」を意味しており、これは個人内変化に関する共変関係を検証するものになります。このように、複数の指標間でレベルや差得点同士の関連を見ることで、相関関係と共変関係をそれぞれ検証することが可能となります。

さらに、複数の指標から抽出したレベルと差得点を用いて、レベルと差得点の関連を表すパスを仮定することもできます。このパスは「指標Aの程度が高い人ほど、その後の指標Bの程度がより大きく増加する」といった、回答者が最初に持っている特徴によって、その後の得点増減がどのように違ってくるかを表しています。つまり、個人差・集団差による個人内変化の違いを検証するものに該当するわけです。

分析モデルの中でレベルと差得点を同時に扱うことで、個人差や個人内の変化について詳細な検証を行うことができることが、潜在差得点モデルの特長になります。

潜在差得点モデルの特長３：「平均への回帰」問題に対応できる

潜在差得点モデルの分析では、複数回測定した一つの指標からレベルと差得点を抽出した後に、同じ指標内のレベルから差得点に対してパスを含めることで、「平均への回帰」といったデータの性質にある程度対処することができます（Könen & Karbach, 2021）。

図８　ある指標内で抽出されたレベルと差得点の間にパスを仮定したモデル

平均への回帰とは、ある指標のデータを複数回取った際、最初の測定次点で極端に高い（あるいは低い）得点を報告したデータは、多くの場合、次の測定次点である程度その極端な状態は保持しつつも、いくらか平均的な値に得点が近づいていく現象を指します。

例えば、ある期間の営業成績が極端に高くなった従業員がいたとしても、次の期間の営業成績は（確かに、ある程度の高さは保ちつつも）いくらか平均的な成績に近づくことがあるでしょう。このような得点の高まりが偶然の要因によって一時的に高まっただけならば、その偶然がその後も続くとは限らず、次の得点はある程度低くなるわけです。

無論、この話題は得点が低い場合でも成立します。いずれにせよ、ある指標において一度極端な値となった場合、次にその指標を測定した際にはいくらか落ち着きを見せて、平均的な値に近づく現象が確認されることが数多くあります。

この問題を踏まえると、２回測定したデータの間の変化には、平均への回帰によって得点が変動している要素が含まれていると考えることができます。そのため、この問題を考慮せずに、この変化を取り上げて分析を進めると、関連の大きさについて推定を誤る可能性が出てきます。

これに関して、潜在差得点モデルでは、同一指標内でレベルから差得点にパスを伸ばすことで、この現象を考慮した分析が可能です。例えば、「従業員間の協調性」のレベルから差得点にパスを伸ばした場合、たいていマイナスのパス係数となります。それが意味することは「もともと協調性が高い人ほど、２回測定した協調性の得点差はよりマイナスの値になっている」、つまり、「もともと協調性が高い人ほど、２回目に測定した協調性の得点は低くなっている」ということです。これは平均への回帰現象そのものになります。

潜在差得点モデルの基にある構造方程式モデルでは、パス係数が持つ特徴は重回帰分析の（標準化）偏回帰係数と同じものになります。「ある影響指標において算出された偏回帰係数は、他の影響指標が成果指標に及ぼす影響を取り除いた、より純粋な影響指標の影響力を表す数値になっている」という特徴を持っているのです （※9）。

すると、潜在差得点モデルの分析において、同じ指標から抽出したレベルと差得点の間にパスを伸ばして分析すれば、平均への回帰によって差得点が変動する影響を取り除くことが可能となり、この問題に対処した上での分析が可能となります。

このように、平均への回帰現象に対してある程度対応して、より正確な検証が可能となることも、潜在差得点モデルの特長です。

潜在差得点モデルの実用例とその解釈

ここで話を戻して、最初の仮想例について、潜在差得点モデルを用いて検証した、指標間の関連に関する結果を見てみましょう （※10）。なお、図が煩雑になるため残差（e）とその間にある相関、そして平均への回帰に対処する同一指標内のレベル→差得点のパスを省略しています。

また、「協調的な風土浸透プロジェクト（不参加・参加）」は、プロジェクトへの参加によって従業員に協調的な風土を浸透させるといった、個人内変化を生むことに焦点を当てたものであるため、従業員たちが最初から持っているレベルにはパスを入れず、従業員たちの個人内変化を表す差得点にのみパスを仮定しています （※11）。

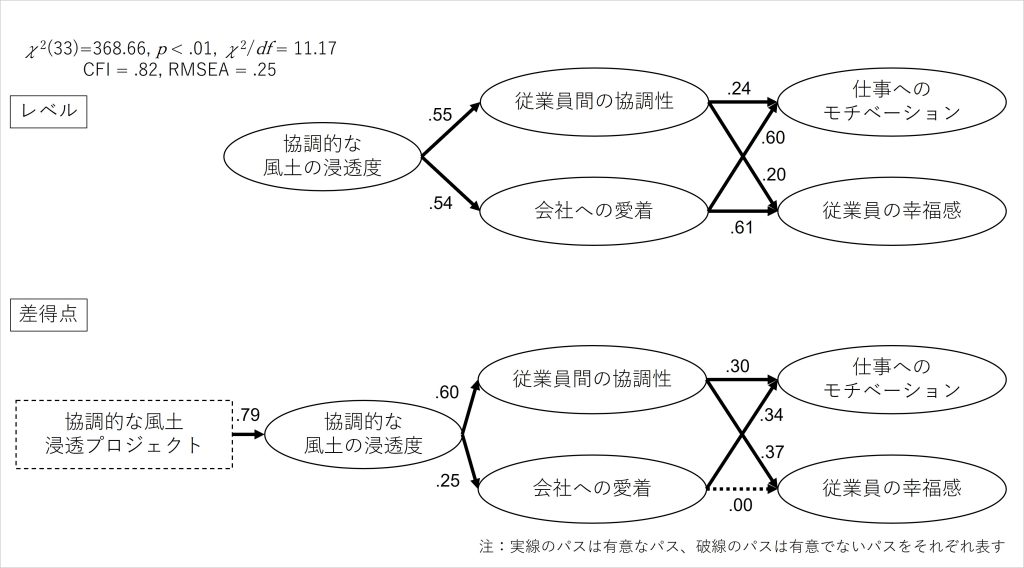
図９　仮説モデルの分析結果

仮説モデルを分析した結果、レベルにおける指標間の関連と差得点における指標間の関連に違いがあることが示されました。レベルでは、パス係数で見て「協調的な風土の浸透度→会社への愛着」の関連が強くなっています。

また、「従業員間の協調性→仕事へのモチベーション」「従業員間の協調性→従業員の幸福感」と「会社への愛着→仕事へのモチベーション」「会社への愛着→従業員の幸福感」の関連の強さをパス係数で比較すると、仕事へのモチベーションや従業員の幸福感とより関連が強いのは、会社への愛着であると判断できます。

この結果はレベル、すなわち相関関係における結果であるため、その意味は「協調的な風土の浸透度をもともと高く評価していた従業員は、従業員感の協調性や会社への愛着も高い状態である」「さらに、会社への愛着が元々高い人は、仕事へのモチベーションや従業員の幸福感も高い状態にあった」ということになります。

他方、差得点における指標間の関連を見ると、パス係数で見て「協調的な風土の浸透度→会社への愛着」の関連が弱いものになっています。また、「従業員間の協調性→仕事へのモチベーション」「会社への愛着→仕事へのモチベーション」の関連をパス係数で比較すると、仕事へのモチベーションの増加に対して従業員間の協調性の増加と会社への愛着の増加が同程度の関連の強さを持っていると判断できます。

加えて、「従業員間の協調性→従業員の幸福感」「会社への愛着→従業員の幸福感」の関連をパス係数で比較すると、「従業員の幸福感の増加と関連していたのは従業員間の協調性であり、会社への愛着の増加は関連していない」ことが示されました。

差得点間の関連は共変関係を表すものであるため、これらの結果が意味することは「協調的な風土の浸透度が従業員の中で高まったとき、従業員間の協調性も増加するが、会社への愛着の増加はそれほど強く対応していない」「仕事へのモチベーションの増加については、従業員間の協調性や会社への愛着の増加がある程度関連しているが、授業員の幸福感の増加には従業員間の協調性しか関連していない」ということです。

ここで、レベルと差得点で得られた結果を比較すると、レベルでは従業員間の協調性よりも会社への愛着がモチベーションや幸福感に強く関連していたことに対して、差得点では会社への愛着は仕事へのモチベーションに対してより強い関連を持っているとは言えず、さらに幸福感については会社への愛着が関連すらしていないという結果になっています。

つまり、「会社への愛着が高い従業員は、幸福感が高い」からと言って、「ある従業員の会社への愛着を増加させることで、幸福感が増加するとは限らない」ということが潜在差得点モデルによって示されたわけです。これこそが相関関係と共変関係を区別して検証する意義であり、興味深い点になります。

さらにここから、「構成したモデルに対して取得したデータがどの程度当てはまっているか」を、適合度指標を用いて検証したり、「取得したデータから見て、構成したモデルに追加すべきパスや相関は存在するか」を修正指標と呼ばれるもので検証したりすることも可能です。これらはさらに掘り下げた分析手法であるため、このコラムの対象外とします。

プロジェクトは変化にどれだけ影響があったかの検証

最後に、差得点のモデルにおいて、「協調的な風土浸透プロジェクト」への参加が、それぞれの指標における得点変化（差得点）にどのような影響を及ぼしたのか、その評価ができることをご紹介します。

方法としては、協調的な風土浸透プロジェクトから各指標の差得点に伸びるパスを仮定し、再分析を行います。そこで得られた分析結果において、追加で仮定したパスそれぞれの「非標準化パス係数」を確認します。このモデル設計において、この非標準化パス係数は「プロジェクトに参加することで、各指標の変化得点は具体的に何点分変わるのか」を意味しています。

ダミーデータを用いてその計算をした結果が、下図になります。

図10　修正後モデルの分析結果

推定された非標準化パス係数を見ると、協調的な風土浸透プロジェクトの参加によって、協調的な風土の浸透度の差得点が+1.19されています。つまり、プロジェクトへの参加は、参加した従業員の協調的な風土の浸透度評価を参加前後で+1.19点分増加させる効果があったということになります。

同様に、プロジェクトへの参加は従業員間の協調性を0.90点増加させ、従業員の幸福感を0.57点増加させる効果があり、会社への愛着や仕事へのモチベーションの得点増加には貢献していなかったことがわかります。協調的な風土を浸透させる目的のプロジェクトでしたが、図らずして、参加した従業員間の協調性も高まり、幸福感の向上まで果たせていたことが実証されたわけです。

他方、会社への愛着や仕事へのモチベーションの向上にはプロジェクトの参加が直接効果を発揮してはいなかったのですが、モデル全体で見ると、協調的な風土浸透度は増加できているため、そこからつながる形で会社への愛着や仕事へのモチベーションが多少高まる効果はあると考えられます。

このように、各指標の変化に対する具体的な得点の違いまで検証を掘り下げられることも、潜在差得点モデルの強みになります。

潜在差得点モデルの問題点

潜在差得点モデルには様々なメリットが存在します。しかし一方で、応用的な分析であるがゆえ、注意すべき問題点がいくつか存在します。これらの問題は、回帰分析において取り上げられるものと同様であり、関連性を検討する分析で常に意識すべきポイントです。なお、これらの問題点は、潜在差得点モデルではなく、それの土台にある構造方程式モデルの問題になっています。

１．十分なサンプルサイズが必要

潜在差得点モデルや構造方程式モデルの分析は、分析による推定を安定させるために必要とされるサンプルサイズが、他の分析と比較して多くなっています。必要なサンプルサイズとしては、少なくとも全体で100名以上は必要であり、200名いれば十分であるといわれています（Kline, 2005） （※12）。取得したデータにおけるサンプルサイズが小さい場合は、この分析は用いないほうが良いでしょう。

２．潜在差得点モデルは、因果関係を保証しない

潜在差得点モデルの分析において、指標間の関連が示されて、モデルの適合度指標が十分に高いものであったとしても、その結果は因果関係を保証しているわけではありません。この分析の内部では、分析モデルが成立すると前提して、指標間の関連の強さやデータとの適合度を算出・推定しています。モデル内の指標の配置を変えれば、それに応じた関連の強さや適合度が算出・推定されるのです。

分析モデルを設計するのは分析者であるため、因果関係を考える上で重要なのは、分析モデルを設計する際に、どのような指標間の展開を想定するかしっかりと検討することです。潜在差得点モデルによって因果関係も検証していくならば、モデルを設計するにあたって、現場の実践知を精査して取り入れ、学術的な知見も踏まえていくことが必要です。因果関係まで含めた探求は、統計学の範疇を超えた模索を徹底していくことが求められます （※13）。

３．酷似した概念を含める際には注意が必要

潜在差得点モデルの分析では、相関が強く酷似した指標同士が影響指標に並んだ際にパス係数の推定に大きな誤差が生じることがわかっています（Grewal et al., 2004）。これは、重回帰分析において生じる多重共線性の問題が、この分析でも生じることを意味しています。これを避けるためには、分析モデルを考える際に、ほぼ同じ意味を表すような酷似した指標を分析に含めないよう意識するのが良いでしょう。

本コラムでは、潜在差得点モデルの内容やその特長について解説していきました。すぐに活用することは難しいかもしれませんが、まずは相関関係と共変関係の違いに意識を向けて、データをより様々な角度から考えられるようなマインドを持つことが大事です。

---

※脚注

1. 観測変数を直接扱う潜在差得点モデルに対して、各時点での測定誤差にも焦点を当てて、各時点で同等な概念を抽出する潜在変数を仮定して検証を行う分析モデル（潜在変化モデルLatent change Model: Hertzog & Nesselroade, 2003; Kievit et al., 2018）の方が、捉えたい概念をより正確に扱えます（c.f., Gollwitzer et al., 2014）。しかし、このコラムは、統計学に詳しくない（主にHR領域の）実務家向けの解説を目的にしています。ここでは「個人内の変化に焦点を当てる」視点や、それに関する分析手法の存在を伝えるために、初学者向けに説明を簡略化し、潜在差得点モデルの解説を行っています。議論を省略している部分があることをご承知おきください。省略した箇所については、別のコラムで機を改めて解説する予定です。
2. 初学者向けの解説として、本コラムで説明する潜在差得点モデルは、２度の反復測定データを扱うものに限定します。３回以上反復測定した場合の潜在差得点モデルについては、Kievit et al. (2018)の概説や、より詳しい解説や分析バリエーションとしてUsami et al. (2019)を参照してください。
3. これに加えて、構造方程式モデリングの大きな特徴は、直接測定していないが測定済みの各指標の共通成分から理論的に抽出できる指標を潜在変数として、分析モデル上で扱える点です。潜在差得点モデル内でも、差得点をモデル上に抽出する際に活用されています。
4. 重回帰分析における標準化偏回帰係数や成果指標の残差の解説は、当社コラム「人事のためのデータ分析入門：『回帰分析～要因を見出すための分析～」（セミナーレポート）を参考にしてください。
5. 厳密にいえば、注釈１で述べた潜在変化モデルのように「各時点で同一の概念を抽出する潜在変数を想定」していなければ、この話は成立しません。その理由は、最初に測定された観測変数にも測定誤差が含まれているためです。なお、潜在変化モデルでは、各時点の指標から得点を抽出する際に測定誤差を除く縦断的因子分析を含むため、この問題は緩和されます。
6. なお、レベルに関しても平均値と分散が推定されるが、レベルは「１回目に測定したその指標の得点」とまったく同じものであるため、推定された平均値や分散は、１回目に測定したその指標の得点の平均値や分散と一致します。したがって、レベルについては推定された平均値や分散を見る意味はほとんどありません。
7. 追加で出力される95%信頼区間を確認したほうが正確です。しかし、ここでは初学者向けに簡単な判断基準を提供するため、検定統計量を参照する方法をまとめています。
8. 有意か否かに関する統計学的な検定の解説は、当社コラム「人事のためのデータ分析入門：『統計的に有意』とは何か」（セミナーレポート）を参考にしてください。
9. 偏回帰係数が持つ特徴については、当社コラム「人事のためのデータ分析入門：回帰分析～要因を見出すための分析～」（セミナーレポート）を参考にしてください。
10. 分析に用いたデータはコラム用に作成したダミーデータであり、実際に取得されたデータで実施した分析ではありません。したがって、ここで示された結果やその解釈内容などは、実践の参考にはなりません。
11. 協調的な風土浸透プロジェクトは四角、他のレベル・差得点を円で表記することは、構造方程式モデルの決まりとして意味があります。しかし、この点は本題とは異なる議論であるため、説明を割愛しています。
12. 「推定される自由パラメータの個数の10倍は必要（Raykov & Marcoulides, 2006）」とする言及もあります。
13. より厳密に因果関係を検証していくならば、反応バイアスなど系統誤差の統制や他の指標による説明可能性の排除など、多くの複雑な手続きを経る必要があります。因果関係の実証方法の探求は、それ自体が現在も研究が進んでいる一大テーマです。

---

引用文献

• Gollwitzer, M., Christ, O., & Lemmer, G. (2014). Individual differences make a difference: On the use and the psychometric properties of difference scores in social psychology. European Journal of Social Psychology, 44(7), 673–682.
• Grewal, R., Cote, J. A., & Baumgartner, H. (2004). Multicollinearity and measurement error in structural equation models: Implications for theory testing. Marketing science, 23(4), 519-529.
• 南風原 朝和（2002）.　心理統計学の基礎　統合的理解のために　有斐閣アルマ
• Hertzog, C., & Nesselroade, J. R. (2003). Assessing psychological change in adulthood: an overview of methodological issues. Psychology and aging, 18(4), 639-657.
• Kline, R. B. (2005). Principles and practice of structural equation modeling (2nd ed.). New York, NY: Guilford.
• Kievit, R. A., Brandmaier, A. M., Ziegler, G., van Harmelen, A. L., de Mooij, S. M., Moutoussis, M., … & Dolan,R. J. (2018). Developmental cognitive neuroscience using latent change score models: A tutorial and applications. Developmental cognitive neuroscience, 33, 99-117.
• Könen, T., & Karbach, J. (2021). Analyzing individual differences in intervention-related 　　changes. Advances in Methods and Practices in Psychological Science, 4(1), 2515245920979172.
• McArdle, J. J. （2009）. Latent variable modeling of diff erences and changes with longitudinal data. Annual Review Psychology, 60, 577-605.
• McArdle, J. J., & Hamagami, F. (2001). Latent difference score structural models for linear dynamic analyses with incomplete longitudinal data. In L. M. Collins & A. G. Sayer (Eds.), New methods for the analysis of change (pp. 139–175). American Psychological Association.
• 村山 航（2012）.　妥当性　概念の歴史的変遷と心理測定学的観点からの考察　教育心理学年報, 51, 118-130.
• Raykov, T., & Marcoulides, G. A. (2006). A first course in structural equation modeling (2nd ed.). Mahwah, NJ: Erlbaum
• Usami, S., Murayama, K., & Hamaker, E. L. (2019). A unified framework of longitudinal models to examine reciprocal relations. Psychological methods, 24(5), 637-657.

---

執筆者

能渡 真澄

信州大学人文学部卒業，信州大学大学院人文科学研究科修士課程修了。修士（文学）。現在は，筑波大学大学院人間総合科学研究科に在籍。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を，他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており，通常では捉えることが困難な，様々なデータの背後にある特徴や関係性を分析・可視化し，その実態を把握する支援を行っている。