数値が低い＝「問題あり」？

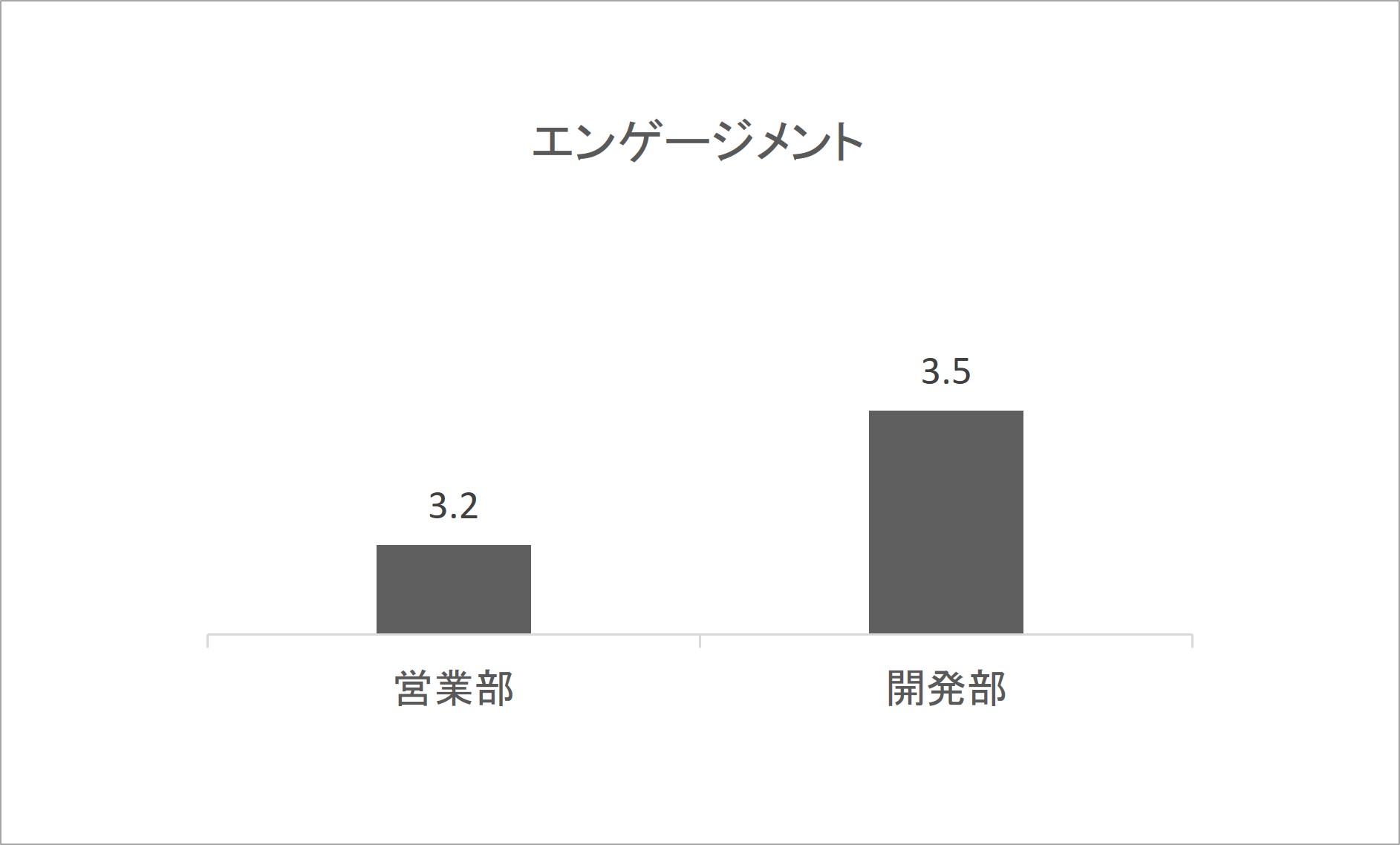
ある会社で、従業員を対象に組織サーベイを行いました。以下は結果のグラフです。営業部と開発部のエンゲージメントの平均値です。

営業部はエンゲージメントの平均値が3.2、開発部は3.5となっています。このグラフを見てどう考え、判断しますか。営業部のほうが平均値は小さいので「営業部にはエンゲージメントに課題があるのでは」と感じるかもしれません。

そこで、営業部のマネジャーを人事が呼び出し、なぜこのような状況になっているのかを一緒に考え、対策を検討してもらおうと考えたとします。「開発部よりも営業部の数値が低かった」ので、営業部に対策を考えてもらおうということです。

ただ、「開発部よりも営業部の数値が低かった」というデータの読み取り方で、本当に問題ないのでしょうか。一見、営業部のほうが低い数値が出ていますが、営業部に問題があると判断して大丈夫なのか、ということを、統計学の「統計的に有意」という考え方で考え直す。これが本コラムのテーマです。

１．統計とはなにか

（1）標本と母集団

まず、統計、より厳密には「推測統計」と呼ばれるものですが、これが一体何を意味しているのかを考えます。

例を挙げましょう。鍋でみそ汁を作っていて、その味が知りたいとします。皆さんなら、どうしますか。全て飲み干しますか。全て飲み干すと味は分かりますが、全部なくなってしまいます。

一般に、鍋のみそ汁の確認には、鍋をよく混ぜてから小皿で味見をする方法を採ります。そのみそ汁の味から、鍋全体のみそ汁の味を推測するはずです。知りたいのは「小皿に取ったみそ汁の味」でなく、「鍋のみそ汁全体の味」ですから、鍋から小皿に取って味見し、全体の味を推測していくわけです。

「小皿に取って、味見をして、みそ汁全体の味を推測する」ことについて、統計学の専門用語で置き換えます。小皿に取ったみそ汁を、統計学の世界では「標本」と呼びます。

一方で、鍋に入ったみそ汁、本来、味を知りたい対象の全体ですが、これは「母集団」と呼びます。母集団の一部が標本になっているという関係性です。

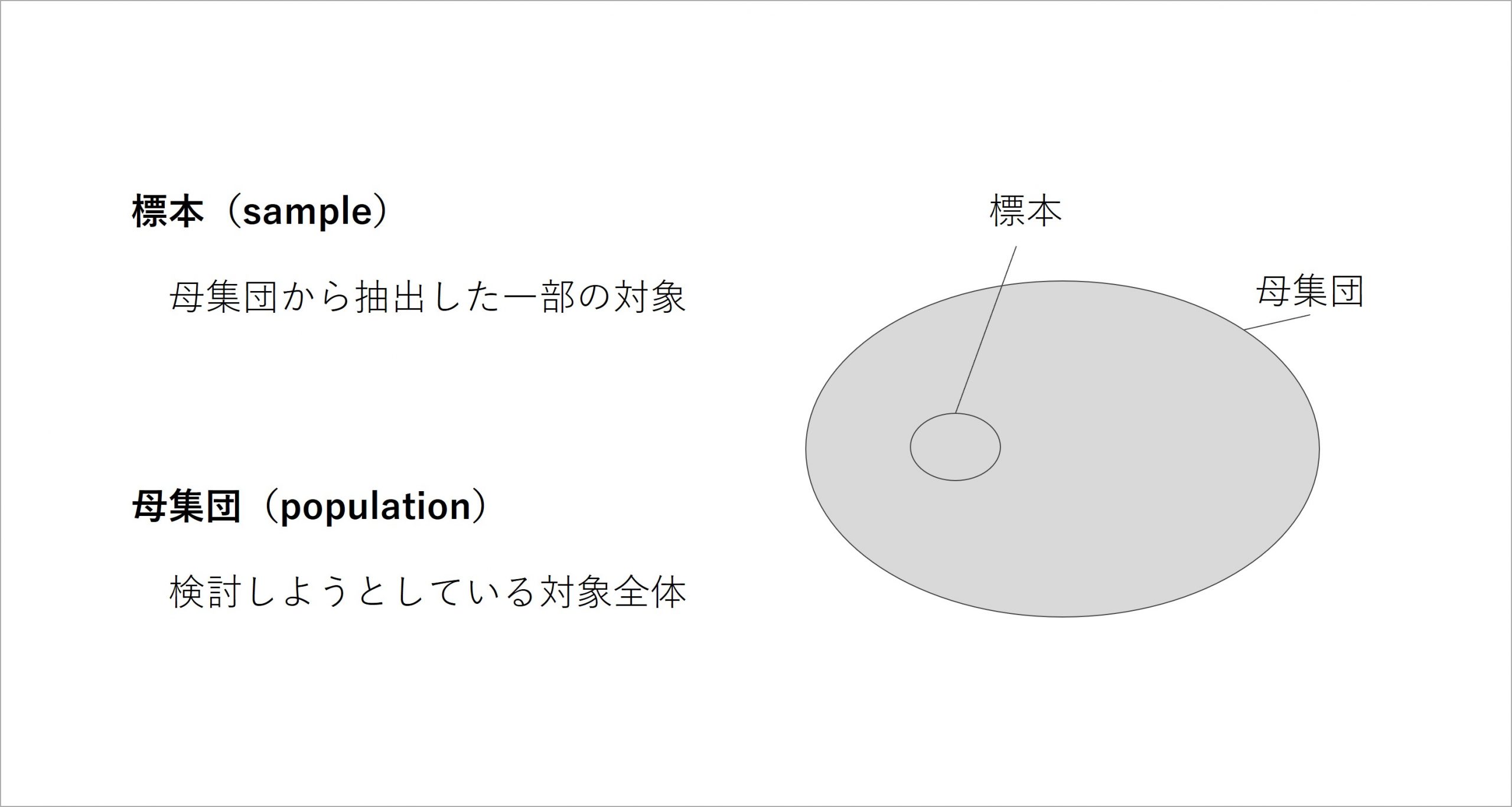
ここまでをまとめると、標本とは、「母集団から抽出した一部の対象」、母集団とは、「検討しようとしている対象全体」を指します。これで、統計を説明するための基本的な概念はおおよそ揃いました。

（2）統計を行う意義

では、推測統計とは何なのでしょう。一言で言えば、「標本で得られた結果が、母集団にも当てはまるかということを検討する」ということです。

組織サーベイでたとえましょう。調査に回答した一部の従業員のデータで見られた特徴が、営業部や開発部全体の特徴として当てはまるのかを検討するということです。

ここで疑問が出てくるかもしれません。なぜ、標本の特徴が母集団に当てはまるかを考えなければならないのか。回答した従業員に見られる特徴で構わないのではないか。

ただし、大きく分けて二つの理由から、この判断には危険が潜んでいます。それらは裏を返せば、推測統計を行う意義でもあります。

一つ目。組織サーベイで回収したデータは、あくまで営業部と開発部の一部の従業員の回答です。しかし、組織サーベイを実施した側としては、全体の状況が知りたいわけです。そのため、一部の結果で判断するのは危険です。

二つ目。標本の中には誤差が含まれる可能性があります。例えば、ある従業員たちが上司に怒られた直後にアンケートに答えたとします。気分が沈んで、いつもと違う回答をしてしまうかもしれません。

そうした誤差がデータには必ず含まれます。その意味で、一度の調査で得られた標本の結果だけで母集団を判断するのは、ミスをおかすおそれがあるのです。

要するに、標本だけでは、母集団を直接検証するものとしては不完全です。標本が不完全なのは認めつつ、それに含まれる誤差を加味してデータを検証する必要があります。

2．有意とは何か

「有意」という語は、正確には「統計学的に有意」と表現されるもので、「標本において観察された傾向が、母集団全体に当てはまると統計学的に判断できる状態」を指します。ここでは、五つのステップに沿って、有意とは何かを説明します。

（1）知りたい仮説を立てる

推測統計の分析では、最初に仮説を立てる必要があります。例えば、「営業部と開発部で、エンゲージメントの高さに違いがある」ということを検証したいとします。これは抽象度を上げると、「A群とB群の平均値には差がある」と表現できます。

ここにおける仮説を「対立仮説」と呼びます。対立仮説は、先ほど説明した母集団という言葉を使って厳密に表現すると、「A群とB群がそれぞれ含まれる二つの母集団の間で、平均値には差がある」となります。

対立仮説は、母集団の間にある差、例に置き換えれば営業部全体と開発部全体のエンゲージメントの平均値の差です。それを得られた一部の標本で検証することになります。

（2）知りたい仮説と反対の仮説を立てる

次に、対立仮説と逆の仮説を立てます。先ほどは、A群の平均値とB群の平均値には差が「ある」という仮説を立てましたが、その逆なので、A群の平均値とB群の平均値には差が「ない」という仮説を立てます。

エンゲージメントの例で言うと、営業部と開発部でエンゲージメントの高さに差が「ない」という仮説です。この仮説を、専門的には「帰無仮説」と呼びます。帰無仮説についても母集団という言葉を用いて表現すると、「A群とB群がそれぞれ含まれる二つの母集団の間で、平均値には差がない」ということになります。

（3）t値を算出する

ここで新しい言葉を出します。「t検定」という分析方法です。t検定とは、2群間の平均値の差を分析し、その差が統計的に有意であるかを検証するものです。今回の例ですと、営業部と開発部のエンゲージメントの高さに差があるかをt検定によって検証します。

t検定では「t値」という値を算出します。ｔ値とは、2群間の平均値の差を、各群に含まれる誤差などのばらつきを考慮して評価した指標です。

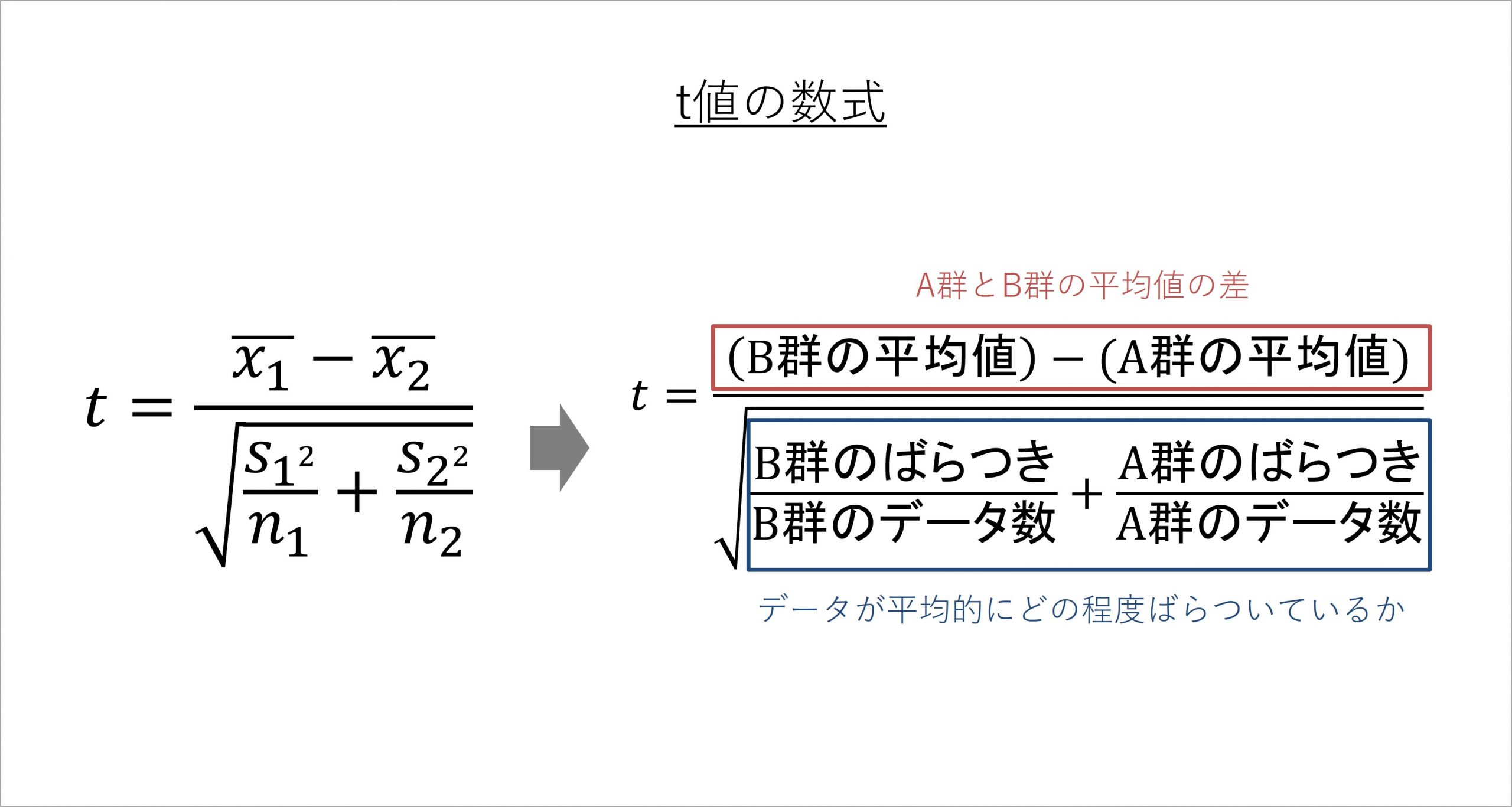
ここからは、このt値の数式を示しつつ、それが何を意味しているのかを説明します。

t値の数式は複雑に見えますが、日本語で表現すると上記のようになります。ｔ値の分子では、A群とB群の平均値の差を見ています。冒頭に挙げた組織サーベイの例では、それぞれのエンゲージメント得点である3.5と3.2を引き算することになります。

問題は分母です。「ばらつき」という言葉が出てきています。これは、「各回答者の得点が、平均からどれぐらい離れているのか」を表すものです。

こういう例を考えてみてください。営業部では、非常に高いエンゲージメントの人から、非常に低いエンゲージメントの人までいる。この状況を、回答にばらつきがあるという意味で、「ばらつきが大きい」と呼びます。

他方で、開発部の中では、およそ平均あたりにみんなの回答が集まっていました。このような場合は、「ばらつきが小さい」と言います。

t値の式の分母に戻りましょう。A群とB群それぞれで、データのばらつきをデータ数で割っています。データ数というのは、シンプルに言うと、何人がその組織サーベイに回答したかということです。例えば、営業部のデータ数は営業部の回答人数を表します。

ばらつきをデータ数で割ったものは、一人一人の回答データが、平均的にどの程度ばらついているかを意味しています。つまりｔ値の数式は、分子は平均値の差、そして分母はデータが平均的にどの程度ばらついているかを表しているのです。

この数式でわかるｔ値の特徴は、平均的なばらつきの程度で平均値の差を割り算したもので、グループ間の平均値の差を評価することにあります。最初の例で挙げたような、営業部と開発部のエンゲージメントの見た目の得点差による判断は、各グループのデータのばらつきを考慮しない直感的なものでした。

対して、ｔ検定で用いられるｔ値は、得点差の評価において、各グループが持つデータのばらつきを割り算に含める点で、一歩掘り下げた判断になっています。

（4）t値の大きさを評価する

検定統計量を算出したら、その値の（絶対値の）大きさを統計学的に評価します。具体的には、「t分布」を参照して、t値の大きさを評価していきます。

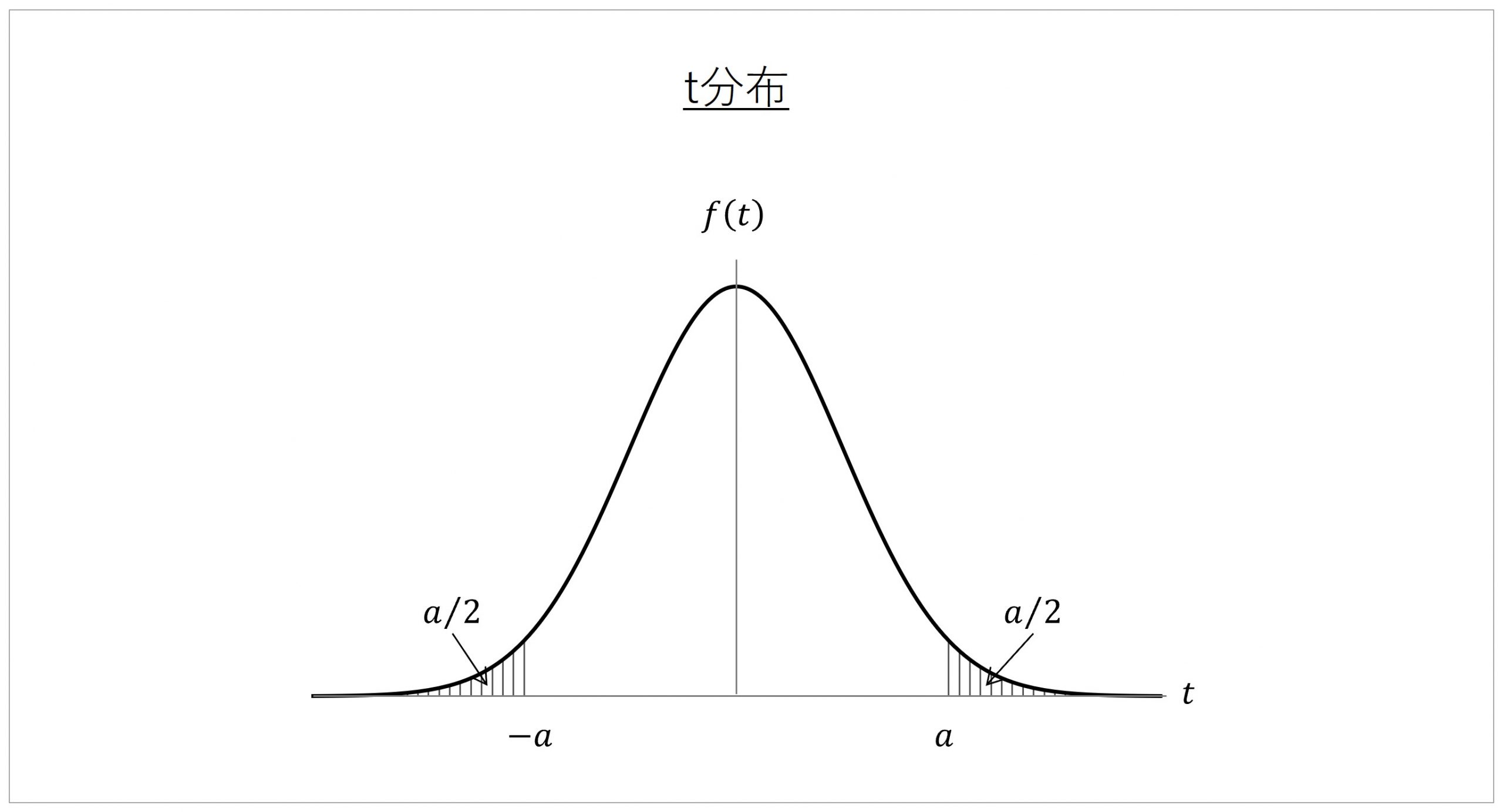t分布は、その名が示すとおり、ｔ値に関する確率の分布を表すものです。横軸がt値、そして縦軸が「2群間の平均値の差が0であることを前提としたときに」、算出されたｔ値がどの程度の確率で生じるのかを表した分布です。

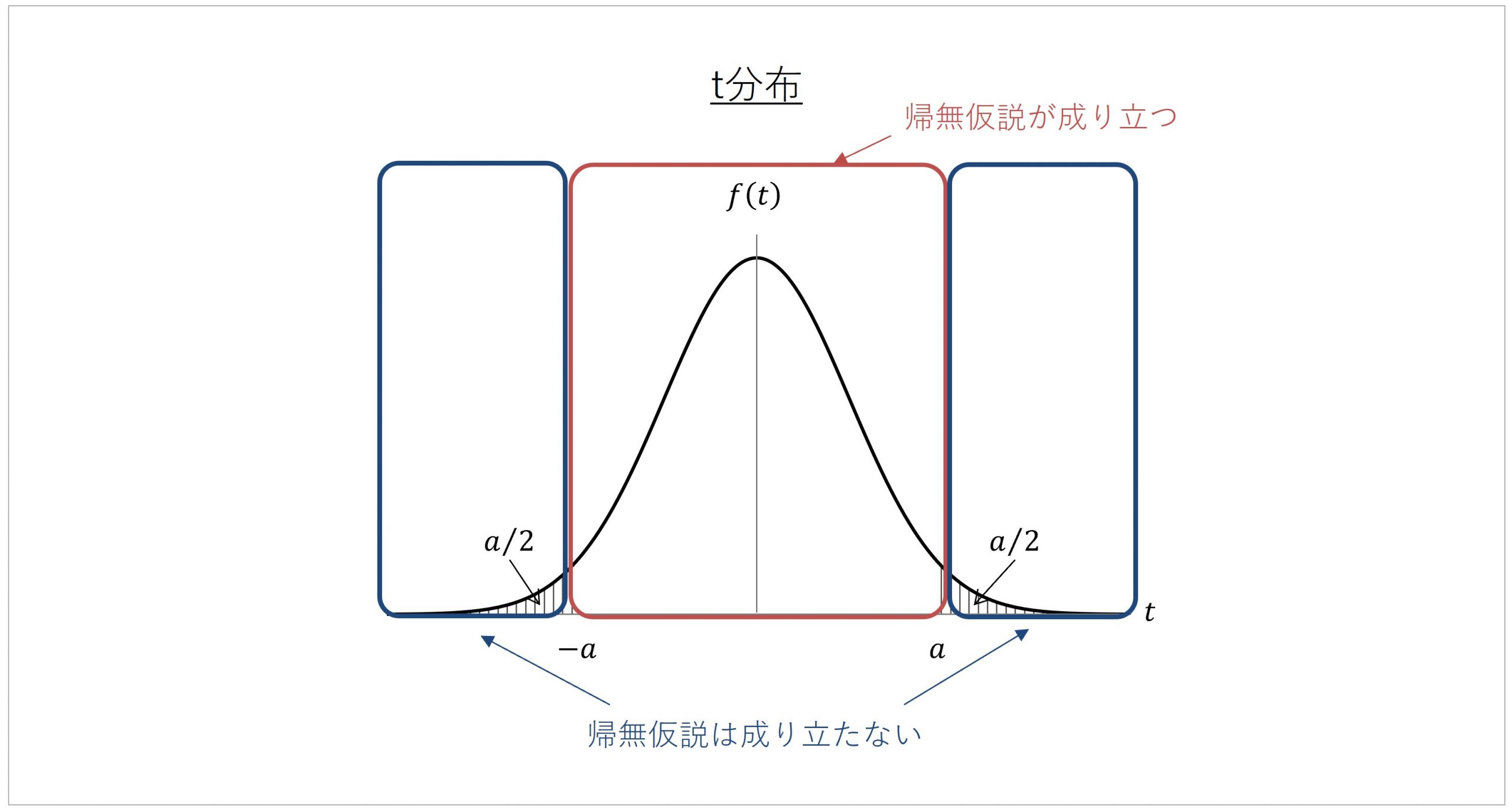
2群間の平均値の差が0であることを前提とした分布であるため、ｔ値が0になる部分がグラフの頂点となる、つまり、そのｔ値が生じる確率がもっとも高いことが示されています。

ここで、ｔ分布の前提「2群間の平均値の差が0であること」は帰無仮説に対応しています。言い換えると、t分布とは、帰無仮説が正しいと仮定して、算出されたt値はどの程度の確率で生じるかを理論的にシミュレーションしたものです。

ｔ分布を用いて、得られたｔ値が生じる確率から仮説の採用可否を考えるのが、ｔ検定のポイントになります。

先に説明した通り、ｔ値はばらつきを考慮した2群間の平均値の差の指標です。「2群間の差が0であること」を前提としたｔ分布においては、大きな数値のｔ値は発生確率がどんどん小さくなります。

仮に、算出されたｔ値が非常に大きい値であったとします。このとき、推測統計の考え方では、「2群間で平均値の差が0という前提において、これほど大きなｔ値が得られるデータが取得されるのはおかしい。つまり、確率を計算する際の“前提が間違っていた”」と判断します。この判断によって、「2群間の平均値の差が0である」という前提が誤りと見なされ、「2群の平均値には差がある」と解釈されるわけです。

逆に、算出されたｔ値の絶対値がいくぶん小さい値であったならば、それは2群間で差がないという前提の上で、確率的にありえるデータが取得されたことになります。「2群間の平均値の差が0である」という前提が誤りだと判断されることはなく、2群間の平均値に差があるという判断は保留されます。

ここで思い出してほしいのですが、「2群間の得点差は0である」という前提が帰無仮説に対応していました。それが誤りと判断された後に取り上げられる「2群間には得点差がある」という解釈は、対立仮説に対応しています。

このように、ｔ検定の検証プロセスでは、算出されたｔ値の大きさをｔ分布にあてはめて考えることで、帰無仮説を棄却して対立仮説を採用するかを判断しています。

（5）p値の小ささを評価する

ｔ検定は、帰無仮説を前提としたｔ分布におけるｔ値の大小で判断を下すという話をしてきました。大きなｔ値が得られたときは帰無仮説が棄却されると説明しましたが、具体的に、どの程度のｔ値が得られたときに帰無仮説が棄却されるのでしょうか。

ｔ検定で得られた分析結果で着目するのは、「ｐ値」と呼ばれる指標です。ｐ値とは、帰無仮説を前提としたｔ分布の中で、算出されたｔ値よりも大きな値が得られる確率を意味しています。

難しく考えなくても、「データから得られたｔ値が生じる確率」と理解しても、実践上問題はないでしょう。絶対値が非常に大きなｔ値の発生確率がとても小さいことは先ほど説明した通りです。言い換えれば、非常に大きなｔ値が得られる確率ｐ値は非常に小さいものになります。

帰無仮説の棄却はｐ値に着目して行われるわけですが、p値はどれぐらい小さければいいのでしょう。これは一つの基準ですが、5％未満だと非常に小さい、すなわち前提が誤っていると判断できる確率と見なされます。ちなみにこれは慣習的な基準です。

営業部と開発部のエンゲージメントの平均値の差についてｔ検定をしたところ、ｐ値が.03となったとします。これは、「営業部と開発部のエンゲージメントに差がない」という帰無仮説を前提としたとき、組織サーベイで得られたデータのような平均値の差が生じる確率は3%であることを意味しています。

ここにおけるｐ値は5％より小さいため、帰無仮説の前提の上では取得できるはずのないデータと見なされ、前提である帰無仮説が棄却されます。そのため、営業部と開発部のエンゲージメントには差がないとは言えない、すなわち営業部と開発部の間には差があると判断されるわけです。

このように、p値が十分に小さいとき、「2群の平均値に差がない」という帰無仮説が棄却されます。それによって、平均値の差がないということはなさそうだ、ということが言え、対立仮説を採択できます。

非常に長い旅路でしたが、こうしたプロセスを通じて、A群とB群の平均値には統計的に有意な差があります、と表現するわけです。

3．統計分析が必要になるケース

今度は、t値（の絶対値）が小さくなる条件について考えます。t値の計算式を見ると、t値がどういう場合に小さくなるのか（＝帰無仮説が棄却できない／有意ではない）が見えてきます。

条件は全部で三つです。一つ目は、平均値の差が小さい場合。これは分子が小さくなるので、t値は小さくなります。t値が小さくなると有意にはなりにくいのです。二つ目が、各群のばらつきが大きい場合。ばらつきが大きいと、分母が大きくなり、t値が小さくなります。三つ目は、データ数が少ない場合。データ数が少ないと、分母が大きくなり、t値が小さくなります。

冒頭の例に戻りましょう。一見、営業部と開発部にエンゲージメントの差があるように見えます。しかし、平均値の差は十分に大きいか。営業部と開発部それぞれのデータのばらつきはどうか。また、データ数はどれぐらいか、疑問に思いませんか。t値の計算式と有意に関する説明をもとにすると、この図だけで判断して大丈夫か不安になるのではないでしょうか。

グラフの見た目だけで判断した場合、エンゲージメントの差が有意でないにもかかわらず、営業部に課題があるとみなすことになりかねません。得られたデータだけで単純に集計してしまうと、場合によっては誤りをおかす可能性があります。

その意味で、統計分析が判断の誤りを小さくしなければならないときに実施したほうが良いと言えます。人事業務だと、従業員への影響が大きいときは統計分析を行ったほうがよいでしょう。

（了）

関連コラム：人事に統計分析が必要なケース3選